II этап урока
Повторение теоретического материала по темам «Арксинус, арккосинус, арктангенс числа» и «Решение простейших тригонометрических уравнений» (7 минут)
1.Математический диктант (устно) (слайды-1) по графикам.
2.Учитель обращается к учащимся с вопросом: «Дайте определение арксинуса числа а».
Учащиеся дают определение.
Определение.Арксинусом числа а называется такое число из отрезка
 , синус которого равен а.
, синус которого равен а.
Учитель: «Сформулируйте свойство нечетности».
Учащиеся: arcsin (-а)=-arcsin а.
Учитель обращается к учащимся с вопросом : «Дайте определение арккосинуса числа а и сформулируйте свойство четности».
Учащиеся дают определение.
Определение.Арккосинусом числа а называется такое число из отрезка
 ,косинус которого равен а.
,косинус которого равен а.
ar ccos (-а)=π-arccos а.
Учитель обращается к учащимся с вопросом : «Дайте определение арктангенса числа и сформулируйте свойство нечетности».
Учащиеся дают определение.
Определение.Арктангенсом числа а называется такое число из интервала (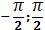 ), тангенс которого равен а.
), тангенс которого равен а.
arctg (-а)=-arctg а.
Учитель обращается к учащимся с вопросом : «Дайте определение арктангенса числа а и сформулируйте свойство четности».
Учащиеся дают определение.
Определение.Арккотангенсом числа а называется такое число из интервала (0; π), котангенс которого равен а.
arcctg (-а)=π-arcctg а.
Комментарии. После этого учитель вывешивает на доску таблицу ( слайд 2).
| arcsin а | Если ≤1, то arcsinа=t ó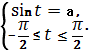
| arcsin (-а)=-arcsin а. |
| arсcos а | Если ≤1, то arccos а=t ó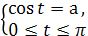
| ar ccos (-а)=π-arccos а. |
| arctg а | arctg а=t ó
| arctg (-а)=-arctg а. |
| arcctg а | arcctg а=t ó
| arcctg (-а)=π-arcctg а. |
№1.Вычислить значения обратных тригонометрических величин (слайд 3).
а)arcsin
| б)arccos 
| в)arctg 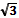
| г)arcctg 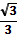
|
| д)2arcsin1 | е)-3arccos0 | ж) arctg1 arctg1
| з)-4arcctg0 |
и)arcsin(- ) )
| к)arccos(- 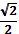 ) )
| л)arctg(- 1) | м)arcctg(- 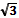 ) )
|
| н)arcsin(cos) | о)arccos (sin  ) )
| п) arctg(cos π) | р)arcctg( sin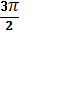 ) )
|
Далее учитель просить перечислить формулы корней простейших тригонометрических уравнений.
Учащиеся формулируют:
Если ≤1, то уравнение sin t=а имеет решение t= arcsinа + πn, n € Ζ.
arcsinа + πn, n € Ζ.
Частные случаи решения тригонометрических уравнений:
1.sin t=1, то t=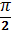 +2 πn, n € Ζ
+2 πn, n € Ζ
2.sin t=- 1, то t=- 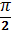 +2 πn, n € Ζ
+2 πn, n € Ζ
3.sin t=0 ,то t= πn, n € Ζ
Если ≤1, то уравнение cos t=а имеет решение t= arccos а+2 πn, n € Ζ.
arccos а+2 πn, n € Ζ.
Частные случаи решения тригонометрических уравнений:
1.cos t=1, то t=2 πn, n € Ζ.
2.cos t=- 1, то t=π+2 πn, n € Ζ
3.cos t=0 ,то t=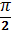 +πn, n € Ζ
+πn, n € Ζ
Уравнение tg t=а имеет решения t=arctg а + πn, n € Ζ.
Уравнение ctg t=а имеет решение t=arcctg а + πn, n € Ζ
Возможный вариант таблицы: (слайд 4)
Если ≤1, то уравнение sin t=а имеет решение t= arcsinа + πn, n € Ζ arcsinа + πn, n € Ζ
| ||
sin t=1, то t=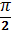 +2 πn, n € Ζ +2 πn, n € Ζ
| sin t=- 1, то t=- 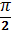 +2 πn, n € Ζ +2 πn, n € Ζ
| sin t=0 ,то t= πn, n € Ζ |
Если ≤1, то уравнение cos t=а имеет решение t= arccos а+2 πn, n € Ζ arccos а+2 πn, n € Ζ
| ||
| cos t=1, то t=2 πn, n € Ζ. | cos t=- 1, то t=π+2 πn, n € Ζ | cos t=0 ,то t=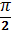 +πn, n € Ζ +πn, n € Ζ
|
| Уравнение tg t=а имеет решения t=arctg а + πn, n € Ζ. | ||
| Уравнение ctg t=а имеет решение t=arcctg а + πn, n € Ζ |