Метод Гаусса.Выбор базисных и свободных переменных.Общее и частное решение

ОБЩЕЕ ЧАСТНОЕ БАЗИСНОЕ РЕШЕНИЯ

Общим решением разрешенной системы уравнений называется совокупность выражений разрешенных неизвестных через свободные члены и свободные неизвестные:

Частным решением системы уравнений называется решение, получающиеся из общего при конкретных значениях свободных переменных и неизвестных.

Базисным решением называется частное решение, получающееся из общего при нулевых значениях свободных переменных.

• Базисное решение (вектор) называется вырожденным, если число его координат, отличных от нуля, меньше числа разрешенных неизвестных.

• Базисное решение называется невырожденным, если число его координат, отличных от нуля, равно числу разрешенных неизвестных системы, входящих в полный набор.

Теорема (1)

Разрешенная система уравнений всегда совместна (потому что она имеет хотя бы одно решение); причем если система не имеет свободных неизвестных, (то есть в системе уравнений все разрешенные входят в базис) то она определена (имеет единственное решение); если же имеется хотя бы одна свободная переменная, то система не определена (имеет бесконечное множество решений).

Решение:

1.Проверяем является ли система разрешенной?

• Система является разрешенной (т.к. каждое из уравнений содержит в себе разрешенную неизвестную)

2. Включаем в набор разрешенные неизвестные - по одному из каждого уравнения.

• В нашем случае мы можем включить в набор разрешенных неизвестных из первого уравнения - x1 и x5, а из второго уравнения только x2. То есть набор может состоять из (x1 x2) или (x5 x2).

3. Записываем общее решение в зависимости от того какие разрешенные неизвестные мы включили в набор.

• допустим мы включили в набор неизвестные x1 и x2, тогда общее решение будет выглядеть так:

4.Находим частное решение. Для этого приравниваем свободные переменные, которые мы не включили в набор приравнять к произвольным числам.

5. Находим базисное решение. Для этого приравниваем свободные переменные, которые мы не включили в набор к нулю.

ü Это метод последовательного исключения неизвестных из системы.

Составим расширенную матрицу системы,будем проводить элементраные преобразования над строками чтобы привести матрицу к виду трапециию.

Столбцы,за исключением последнего,можно переставлять местами,фиксируя при этом над матрицей где какая переменная.

В круг.скоб. - * на 3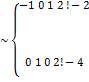- круг скобки.

2ую и 3ю строку и сложить с 1ой.

Возможнны три случая:

1)r(A)≠r(A!B) – система не совместна

2)r(A)=r(A!B) – система совместна

а) r=n(число переменных),то система определена

Восстанавливаем систему по полученой матрице начиная с последнего уравнения и поднимаясь к первому последовательно находим неизвестные

б) r,то система не определена.Восстановим систему по полученой матрице выбираем r переменную таким образом,чтобы определитель составленный из коэфицентов при этих переменных был отличен от нуля.назовем эти переменные базисными,остальные переменные свободные.Выбор базисных переменных не однозначен начиная с последнего уравнения последовательно выразим базисные переменные через свободные.Получим общее решение системы.

… r(a)=r(A!B)=2

r=2 – система не определена

Х1,х2-базисные х3,х4 – свободные

- общее решение системы

Подставляя вместо свободных эл-ов любые числа и вычисляя базисные переменные,получим частные решения системы.

Пусть х3=0, х4=0