Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц

1.Понятие матрицы. Виды матриц. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.

.Матрицей размера mxn наз-ся прямоуг.таблица чисел,сост.из n-строк и m-столбцов.Эл-ты м-цы – числа,составл.м-цу. М-цы обознач.прописными(загл.)б-ми лат.алфав.,напр.:А,В,С,..,а для обознач.эл-тов м-цы исп.строч.буквы с двойной индексацией:а_ij,где i-номер строки, j – номер ст-ца. М-ца наз-ся невырожденной (неособенной, если |A|≠0. При |А|=0 – вырожденная (особенная) м-ца.

Виды м-цы: м-ца(вектор)столбец – м-ца,сост.из одного столбца; м-ца(вектор)строка – м-ца,сост.из одной строки; квадр.м-ца n-го порядка – м-ца,ч-ло стр.которой=ч-лу ст-в и =n.; диагонал. – все недиагонал.эл-ты квадр.м-цы равны 0.; единич.(обознач.Е) – все диагонал.эл-ты диагонал.м-цы =1; нулевая – м-ца,любого размера, если все её эл-ты равны 0.

Трансп.м-цы – это смена местами строк и ст-в с сох-м порядка следования эл-тов. А – исходная, А’(А^т)-транспонир. Если А м-ца имеет размер mxn, то А’ м-ца – nxm.

Равенство м-ц:две м-цы одинак.размера наз.равными,если они равны поэлементно.

Сложение м-ц: (одинак.размера)Складываем соотв.эл-ты.

Умножение на число: все эл-ты м-цы умнож.на это число. (Общ.множитель всех эл-тов выносится за знак.м-цы).

Умножение 2-х м-ц: произведение м-цы А_mxn на м-цу В_nxp наз-ся м-ца С_mxp,каждый эл-т которой равен сумме произведений эл-в i-строки на соотв.эл. j – столбца. Перемножать можно только такие м-цы,когда число столбцов 1-ой м-цы равно числу строк 2-й м-цы. Произведение м-ц не коммуникативно. 2х3 3х7 не = 3х7 2х3,т.к. 7 не = 2.

Возвед.квадр.м-цы в степень. (только квадр.) А^m = А_* А_* ..А. m раз.

2. Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца.

Опред.1-го порядка (м-цы 1-го порядка) наз-ся эл-т этой м-цы а₁₁. Е=(1),|E| = detE=1

A=(0),|A|=0.

Опред.2пор.наз-ся ч-ло,кот.считается след.образом |A|=a_11*a₂₂ – a_12*a_21.

Опред.3пор.наз-ся ч-ло,кот.наход.по ф-ле (когда вычёркивают по пересечению..)

Теор.Лапласа(о разлож.опред.) Опред.квадр.м-цы равен сумме произведений эл-тов какой-либо ст-ки или ст-ца на их алгебраич.дополнения.

_^3 = a_11*A₁₁ + a_12*A₁₂ + a_13*A₁₃ (_^3 = a_{11 *}M₁₁ – a_{12 *}M₁₂ + a_{13 *}M₁₃)

Замечание:Для _^-ной м-цы (то есть такой,в кот.под эл-ми гл.диагонали-нули)опред-ль равен произвед.диагонал.эл-тов(эл-тов гл.диаг.)

Св-ва опред-й: 1)При трансп.опред-ль м-цы не меняется.

2)Если в м-це есть нулевая строка или нулевой столбец,то опред-ль такой м-цы =0.

3)Если в м-це поменять местами 2 ст-ки или ст-ца с сохр-м порядка след.эл-тов,то опред-ль поменяет знак на противопол.

4)Если в м-це есть 2 одинак.строки или столбца,то опред-ль такой м-цы =0.

5)Общ.множ-ль эл-тов какой-либо ст-ки или ст-ца можно вынести за зн.опред-ля.

6)Если к эл-там какой-либо стр.или ст-ца прибавить эл-т др.ст-ки или ст-ца,умноженные на любое число,то опред-ль не изм.

Квадратная матрица и ее определитель. Особенная и неособенная квадратные матрицы. Присоединенная матрица. Матрица, обратная данной, и алгоритм ее вычисления.

Определители квадр.м-ц:

Опред.1-го порядка (м-цы 1-го порядка) наз-ся эл-т этой м-цы а₁₁. Е=(1),|E| = detE=1

A=(0),|A|=0.

Опред.2пор.наз-ся ч-ло,кот.считается след.образом |A|=a_11*a₂₂ – a_12*a_21.

Опред.3пор.наз-ся ч-ло,кот.наход.по ф-ле (когда вычёркивают по пересечению..)

Св-ва опред-й: 1)При трансп.опред-ль м-цы не меняется.

2)Если в м-це есть нулевая строка или нулевой столбец,то опред-ль такой м-цы =0.

3)Если в м-це поменять местами 2 ст-ки или ст-ца с сохр-м порядка след.эл-тов,то опред-ль поменяет знак на противопол.

4)Если в м-це есть 2 одинак.строки или столбца,то опред-ль такой м-цы =0.

5)Общ.множ-ль эл-тов какой-либо ст-ки или ст-ца можно вынести за зн.опред-ля.

6)Если к эл-там какой-либо стр.или ст-ца прибавить эл-т др.ст-ки или ст-ца,умноженные на любое число,то опред-ль не изм.

Опред.квадр.м-цы равен сумме произведений эл-тов какой-либо ст-ки или ст-ца на их алгебраич.дополнения.

_^3 = a_11*A₁₁ + a_12*A₁₂ + a_13*A₁₃ (_^3 = a_{11 *}M₁₁ – a_{12 *}M₁₂ + a_{13 *}M₁₃)

М-ца наз-ся невырожденной (неособенной, если |A|не=0. При |А|=0 – вырожденная (особенная) м-ца.

Присоедин.м-ца. А^~ присоединённая для м-цы А,если она сост.из алгебраич.дополнений к эл-там транспонир.м-цы. Замеч.:чтобы быстро найти присоедин.м-цу для квадр.м-цы 2-го порядка надо поменять местами эл-ты на гл.диагонали, а перед другими двумя Эл-ми поменять знак на противоп.

Обратная м-ца. А^-1 наз-ся обратной для м-цы А, если произведение этих м-ц в любом порядке есть Единичное. А_*А^-1=А^-1_*А=Е Замечание:если опред-ль м-цы А не равен 0,то такая м-ца наз-ся невырожденной (неособенной).

ТЕОР.для того, чтобы квадр.м-ца А имела обратную,необх.и достат., чтобы она была невырожденной. А^-1 нах-ся о формуле: А^-1=1/|А| _* А^~ (сначала находим опред-ль (|A|), затем присоед.м-цу (А^~), потом по ф-ле находим обр.м-цу А^-1)

4. Понятие минора k-го порядка. Ранг матрицы (определение). Вычисление ранга матрицы с помощью элементарных преобразований. Пример.

Минором M_ij эл-та a_ij квадр.м-цы A n-ого порядка наз-ся опред-ль квадр.подм-цы n-1-го порядка, полученной из исходной вычёкиванием i-строки и j-ст-ца.

Если в м-це А размера mxn выделить какие-либо k ст-к и k ст-в (k ≤ min (m,n)),то опред-ль подм-цы из получаемых на пересечении этих строк и ст-в эл-в наз-ся минором k-го порядка м-цы А.

Ранг м-цы - это наивысший порядок минора м-цы отличный от нуля. (Минор м-цы – то опред-ль квадр.подм-цы). r(А) = n

Ранг м-цы равен максимал.числу лин.независ.ст-к или ст-в м-цы.

Эл.преобраз.:1)отбрас.нулевой строки или ст-ца. 2)Трансп.м-цы, 3)Сложение(или вычит.)эл-тов какой-либо строки или ст-ца с соотв.эл-ми др.стр.(ст.), умноженными на какое-то(любое)число., 4)Смена местами стр-к или ст-в м-цы с сохран.порядка след.эл-тов в них.

ТЕОР.Ранг м-цы не меняется при эл.преобраз.

Опр:М-ца наз-ся ступенчатой,если под эл-ми гл.диагонали такой м-цы только нул.эл-ты или эл-тов вообще нет. Замечание:Элементарн.преобразованиями любая м-ца приводится к ступенчатой. В такой ступенчатой матрице ранг это число строк в ней. Это число совп.с рангом исх.м-цы,т.к.при элементар.преобр.ранг не меняется.

 

*2 ( 2 -4 1 5 3)<

| ( 0 -1 3 0 2) |

+ (-4 5 7 -10 0) | ~

(-2 1 8 -5 3)</

 

(2 -4 1 5 3) (2 -4 1 5 3)

(0 -1 3 0 2)*3 (0 -1 3 0 2)

~ (0 -3 9 0 6) - ~ (0 0 0 0 0)

(0 -3 9 0 6) - (0 0 0 0 0)

 

(2 -4 1 5 3)

(0 -1 3 0 2)

~ (0 0 0 0 0) > r(A)=2,т.к.

(0 0 0 0 0) 2 строки в ступенч.м-це.

Линейная независимость столбцов (строк) матрицы. Теорема о ранге матрицы.

l1=(a11,a12,a13,a14,..,a1n) – 1-я строка; l2=(a21,a22,a23,a24,..,a2n) – 2-я строка. lm=(am,am2,am3,am4,..,amn) Линейной комбинацией строк м-цы наз-ся выраж.… λ 1 * k1+ λ 2k2+… + λ m-1km -1+ λ mkm , где все λ -это числа.

Собственные векторы и собственные значения матрицы. Характеристическое уравнение матрицы.

Число Y наз-ся собственным зн-ем оператора А~ (м-цы А),соответствующим в-ру Х. Метод вычисления собств.зн-ий и собств.в-ров.Т.к. Хnx1=Еnx1 * Хnx1, то АХ=YEX… Ур-е |A-YE|=0 – характеристическое ур-е м-цы. Из него находим Y и далее по ур-нию (A-YE)X=0 находим соотв.ненул.в-р…

Ф.2(... ... ... ... );

(a_m1 a_m2 .. a_mn)

(x₁)

X= (x₂)

Ф.3 (....);

(x_n)

(b₁)

B= (b₂)

Ф.4(....);

(b_m)

называются собственно матрицей системы, матрицами-столбцами переменных и свободных членов.

Решение системы:а)методом обр.м-цы. Ур-е в матричной ф-ме имеет вид АХ+В. Найти обр.м-цу. И найдём Х по ф-ле Х=А^-1В,(т.е.х₁,х₂,х₃.)

б)По ф-ле Крамера. Найти определитель системы _^=|A|. Если он не=0,то сист.имеет единств.реш. Далее вычислить опред-ли м-ц _^1,_^2,_^3,полученных их м-цы А,заменой соотв-но 1-го,2-го и 3-го ст-цов столбцом своб.членов. Далее по ф-лам Крамера:х1=^1/_^,х2=^2/_^, х3=^3/_^.

Расширенной м-цей системы наз.м-ца (А|В),полученная из м-цы сист.А добавлением к ней ст-ца членов этой системы,т.е. (А|В)=(ф.2|ф.4)

Теорема Кронекера-Капелли.Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы.

r<m – ур-я с-мы(строки расш.м-цы)зависимые;

r=m –ур-я с-мы (стр.расш.м.)независимые;

r(A)не=r(A|B)- с-ма несовм-ная;

r(A)=r(A|B)=r – с-ма совм-ная;

r<n – с-ма неопред.(бескон.мн.реш.);

r=n – с-ма опред-ная (единств.реш.)

Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.

Если система лин.ур-й имеет единств.решение Х=(х₁,х₂,…х_n),то такая сист.наз.определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист.не определённая.

9. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.

Метод Гаусса –метод послед-го исключ.переменных.

Сначала(на 1-м шаге прямого хода Гаусса) из всех ур-ний,кроме 1-го исключается переменная х₁. Потом (на 2 шаге) из всех ур-й,кроме первых 2-х исключается переменная х₂ и т.д.,пока последнее ур-е не приобретёт вид:С _* Х_n=b_m,если ч-ло С=0, а b_m не=0,то с-ма не совместная,т.е.нет решений. Если С=0 и b_m=0,т.е. 0_*Х_n=0,то с-ма неопределённая,т.е. имеет бескон.мн.реш.,то с-ма совместно-определённая. В этом сл-е Хn=b_n/C

Полученное зн-е Х_n подстав.в предпосл.ур-е,находим Х_n-1и тд.,пока не получ.все неизв-е.

Обратный ход Гаусса. Из м-цы ступенч.вида записывается ур-е. Далее,начиная с конца находим все переменные. Допустим Х₄. Подставляем в верхнее и нах-м Х₃ и т.д.

Метод Гаусса — Жордана исп-ся для реш.квадр.систем лин.ур-ний, нахождения обрат.м-цы, отыскания ранга м-цы. Метод явл-ся модификацией метода Гаусса. Назван в честь Гаусса и Жордана.

Теорема Кронекера-Капелли.Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы.

r<m – ур-я с-мы(строки расш.м-цы)зависимые;

r=m –ур-я с-мы (стр.расш.м.)независимые;

r(A)не=r(A|B)- с-ма несовм-ная;

r(A)=r(A|B)=r – с-ма совм-ная;

r<n – с-ма неопред.(бескон.мн.реш.);

r=n – с-ма опред-ная (единств.реш.)

Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.

Если система лин.ур-й имеет единств.решение Х=(х₁,х₂,…х_n),то такая сист.наз.определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист.не определённая.

10. 10. Решение систем п линейных уравнений с п переменными с помощью обратной матрицы (вывод формулы Х=А ^–1В).

Рассм.с-ма лин.ур.,в кот.ч-ло ур-ний = ч-лу неизв-х. Тогда м-ца с-мы (сост.из коэф-в при неизв-х,когда в 1-м ст-це коэф-та Х₁, во 2-м коэф-та Х₂ и т.д.) квадратная.

Если м-ца с-мы невырожденная, то реш.с-мы ст-ц неизв-х

Х=А^-1В, где В – ст-ц своб.чл-в.

Для получ.реш-я с-мы (ф.1) при m=n в общ.виде предположим, что квадр.м-ца с-мы А_nxn невырожд.,т.е. её опред-ль |A|не=0. В этом сл-е сущ-ет обр.м-ца А^-1.

Умножая слева обе части матричного равенства (ф.5) на м-цу А^-1,получим А^-1(АХ)= А^-1В. Т.к. А^-1(АХ)=(А^-1А)Х=ЕХ=Х, то реш-м с-мы методом обр.м-цы будет м-ца-столбец Х= А^-1В.

А_mxn*Х_nx1=В_mx1 <=> (ф.1)

(a₁₁x₁+a₁₂x₂+…+ а_nx_n=b₁

(a₂₁x₁+a₂₁x₂+… +a_2nx_n=b₂

(….

(а_mx₁+а_2mx₂+… +а_mnх_n=b_m

(а₁₁х₁+ а₁₂х₂ +…+а_1jx_j+...+а_1nx_n=b₁; (ф.5)

(а₂₁х₁+а₂₂х₂+…+а_2jx_j+…+а_2nx_n=b₂;

(...........

(а_i1х₁+а_i2х₂+…+a_ijx_j+…+a_inx_n=b_i;

(...........

(а_m1х₁+а_m2х₂+…+а_mjx_j +…+а_mnx_n=b_m.

11. Теорема и формулы Крамера решения системы п линейных уравнений с п переменными (без вывода).

Ф-лы Крамера решения с-м из n ур-ний с n неизв.

Обозначим опред-ль м-цы системы |А|=^. Если (опред-ль м-цы) ^не=0,то сист.имеет ед.реш. хi=^i/^, i=1...n, где ^1,^2, ^3,...^n побочные опред-ли.… Для вычисл.^3 в м-це с-мы 3-й ст.заменяют ст.св.чл-в. Затем находят х1,х2,х3… Замечание: (Из метода гаусса 0*Хn=0,то бескон.мн.реш. Формально Хn=0/0 – неопред.)

Понятие функции, способы задания функций. Область определения. Четные и нечетные, ограниченные, монотонные функции. Примеры.

Постоянной величиной наз-ся вел-на,сохраняющая одно и то же зн-е (число «пи»). Если вел-на сохр.пост-е зн-е лишь в усл-ях данного процесса,то в этом сл-е она наз-ся параметром.

Переменной наз-ся вел-на,кот.может принимать различные числ.зн-я.

Понятие функции. Опр: Если каждому эл-ту Х множества Х(х принадл. Х) ставится в соотв-е вполне опред-ный эл-т у множества Y (y принадл. Y),то говорят, что на мн-ве Х задана функция y=f(x).

При этом х наз-ся независимой пер-й (аргументом),y-зависимой пер-й, а буква f обозн-т закон соответствия.

Мн-во Х наз-ся областью определения ф-ции, а мн-во Y – обл.зн-й ф-ции.

Под обл-ю опред-я ф-ции подразумевается обл.допустимых зн-й независ.переменной х, т.е. мн-во таких зн-й х,при кот.ф-ция y=f(x) вообще имеет смысл.

Способы здания фун-й. а)аналитический с.- если ф-ция задана ф-лой вида y=f(x). Одна ф-ция может иметь (допустим)2 аналитических выражения.

б)Табличный – состоит в том,что ф-ция задаётся таблицей, содержащей зн-я аргумента х и соотв.зн-я ф-ции f(x).

в)Графический – состоит в изображении графика ф-ции – мн-ва точек (х;у) плоскости, абциссы которых есть зн-я аргумента х, а ординаты – соотв-е им зн-я ф-ции y=f(x).

г)Словесный – если ф-ция описывается правилом её составления,напр.ф-ция Дирифле:f(x)=1, если х-рационально; f(x)=0, если х – иррационально.

Чётность и нечётность.

f(-x)=f(x) – чётная, график симметричен относит. Оу. (х²)

f(-x)=-f(x) – нечётная, гр.симметричен относит. Начала координат. (х³)

В противном сл-е ф-ция y=f(x) наз-ся ф-цией общего вида.

Монотонность.

Ф-ция y=f(x) возрастает на промеж.Х, если большему зн-ю аргумента соотв. большее зн-е ф-ции.

Ф-ция y=f(x) убывает на промеж.Х, если большему зн-ю аргумента соотв. меньшее зн-е ф-ции.

Ф-ции возрастающие или убыв-е наз-ся монотонными ф-циями.

Ограниченность.

Ф-ция f(x) – ограниченная на промеж.Х, если сущ-ет такое полож.ч-ло M>0, что |f(x)|<и равно М для любого х принадлежащего промежутку Х. Например, ф-ция y=sinx ограничена на всей числ-й оси,т.к. |sinx|<и равно1 для любого х, принадл-го R.

Периодичность.

Ф-ция периодическая с периодом T не=0, если для любых из обл.опред-я ф-ции f(x+T)=f(x). Напр., ф-ция у=sinx имеет период T=2«пи»,т.к. для любых х sin(x+2«пи»)=sinх.

 

Понятие элементарной функции. Основные элементарные функции и их графики (постоянная, степенная, показательная, логарифмическая).

Элементарная ф-ция.

Алгебраической наз-ся ф-ция, в кот. над аргументом производится конеч.ч-ло алгебраич.действий. К ч-лу алг.ф.относят:1)целая рациональная ф-ция:… Преобр-е графиков. 1.Гр.ф-ции у=f(х+а)есть гр. у=f(х), сдвинутый (при а>0… 2.Гр.ф-ции у=f(х)+bесть гр. у=f(х), сдвинутый (при b>0 вверх, при b<0 вниз) на |b| ед-ц параллельно оси Оу.

Уравнение линии на плоскости. Точка пересечения двух линий. Основные виды уравнений прямой на плоскости (одно из них вывести).

Точка пересеч-я двух линий:система двух прямых A1x+B1y+C1=0;A2x+B2y+C2=0 – если прямые не параллельны, т.е. А1/А2 НЕ РАВНО В1/В2, то реш-е системы… Осн.виды урав-ий прямой на плос-ти: 1)Урав-е пря-й, проход-щей через данную… 16.Предел последовательности при n-→∞ и предел функции при x→∞. Признаки существования предела…

Геометрический смысл предела числ. посл-ти

Нер-во | a_n -A|<E<=> -E<a_n -A <E <=> A-E< a_n<A_n +E

Границы (A-E; A +E) означают, что практически большинство членов посл-ти находящихся в E – окрестности в т.А, а вне этой окр-ти находится ограниченное число членов посл-ти, находится вне этой окр-ти

1;1/2;1/3; ….1/10……1/11;1/12

вне Е окр-ти принадлежат Е-окр.

Предел функции в бесконечности

A= lim f(x)

Число А называется пределом функции при x→∞ .,если для любого даже сколь угодно малого полож числа E>0 , найдется такое полож число S>0 (зависящее от Е, S=S (E)), что для всех х таких что |х|>S

верно нер-во |х|>S

|f(x)-A|<E

Признаки существования предела

Теорема2.Если в некоторой окрестности точки х0 функция заключена между двумя функциями φ(х) и ψ(х), имеющими одинаковый предел А при… Пусть приx→х0 lim φ(х)=А, lim ψ (х)=А Это означает, что для любого Е>0 найдется такое число σ>0, что для всех х≠х0 и удовлетворяющих…

Бесконечно малые величины (определение). Свойства бесконечно малых (одно из них доказать). Бесконечно большие величины, их связь с бесконечно малыми.

Функция y=f(x) называется БМпри определенном стремлении аргумента, если рано или поздно ее значение по модулю будут меньше любого наперед выбранного полож числа Е, т.е. |f(x)|<E, то

lim f(x)=0

Св-ва БМ величин

2.произведение БМ величины на ограниченную функцию есть величина БМ 3.частное от деления БМ величины на функцию, предел который отличен от нуля,… Доказательство 1 св-ва.

Теорема о связи между БМ и ББ величинами

f(x) = A+ α(х,) 2.Если функцию можно представить как сумму числа А и БМ α(х,) при… 19. Второй замечательный предел, число е. Понятие о натуральных логарифмах.

Второй замеч.предел.

an=(1+1/n)n. Данная послед-ть монотонно возрастает и ограничена. а1=2, а2=2,25, а3≈2,37…, а4≈2,44…, а100≈2,71, а1000≈2,71,… limn→∞(1+1/n)n≈2,71 (Эйлерово число). Опр:Числом е (2-м замечат.пред-м)наз-ся предел числовой последовательности e=limn→∞(1+1/х)х.

Непрерывность функции в точке и на промежутке. Свойства функций. Непрерывных на отрезке. Точки разрыва. Примеры.

Функция f(x) называется непрерывной в т.x₀ , если она удовлетворяет след 3 условиям:

_1. определена в т. x_0.

2.имеет конечный предел функции при x→х₀

3. этот предел равен значению функции f(x₀) в т. x₀ т.е. lim f(x)= f(x)

Непрерывность функции на отрезке

Свойства функции y=f(x) непрерывна на [a.b] 1.Если функция y=f(x) непрерывна на [a.b],то она ограниченна на этом… 2.Если функция y=f(x) непрерывна на [a.b],то она достигает своего max или min значения.

Дифференцируемость функций одной переменной. Связь между дифференцируемостью и непрерывностью функции (доказать теорему).

Нахождение производной функции называется дифференцированием этой функции.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция дифференцируемая во всех точках промежутка х, называется дифференцируемой на этом промежутке.

Связь между дифференцируемостью и непрерывностью функции.

Док-во. Согласно определению производной y’= lim ∆y/∆x ∆x→0

Основные правила дифференцирования функций одной переменной (одно из этих правил доказать).

1.Производная постоянной равна нулю,т.е. с’=0. 2.Произв.арг-та равна 1,т.к. х’=1. 3.Произв-я алгебрач.суммы конечного ч-ла дифференцируемых ф-ций равна такой же сумме производных этих ф-ций, т.е.…

Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функций.

Формулы производных основных элементарных функции.

2.x’=1 3.(u+v)’=u’+v’ 4.(uv)’=u’v+uv’

Производная сложной функции

y’=f’(u)’*ux’ y’=lim ∆y/∆x= lim ∆y*∆u/∆x*∆u= lim… (если∆x→0,то и ∆u→0,т.к.u= φ(x)- непрерывна)

Теоремы Ролля и Лагранжа (без доказательства). Геометрическая интерпретация этих теорем.

1)непрерывна на отр.[а;b]; 2)дифференцируема на инт-ле(а;b); 3)на концах отрезка принимает равные зн-я,т.е. f(a)=f(b).

Теорема Лагранжа.

1)непрерывна на отр. [а;b]; 2)дифференцируема на инт-ле(а;b); Тогда внутри отрезка сущ-ет по крайней мере одна такая точка ξпринал.(а,b), в кот.производная равна частному от…

Достаточные признаки монотонности функции (один из них доказать).

Тео-ма (достаточное условие убыв.фун-и). Если производная диф-мой фун-и отрицательна внутри некоторого промежутка Х, то она убывает на этом…

Определение экстремума функции одной переменной. Необходимый признак экстремума (доказать).

Опр.экстремума ф-ции одной пер-ной.

Опр1:Точка х0 наз-ся точкой максимумаф-ции f(x),если в некоторой окрестности точки х0 выполняется неравенство f(x)≥f(x0). Опр2:Точка х1 наз-ся точкой максимума ф-ции f(x),если в некоторой окрестности… Значения ф-ции в точках х0 и х1 наз-ся соотв-но максимумом и минимумом ф-ции. Максимум и минимум ф-ции объединяются…

Необходимое усл-е экстремума.

Точки, в кот.выполнено необх.усл-е экстремума,т.е. производная равна нулю или не сущ-ет, наз-ся критическими (или стационарными). Эти точки должны… Первое достаточное условие экстремума. Теорема. Если при переходе через точку… Доказательство.Пусть производная меняет знак с плюса на минус, т.е. в некотором интервале (а, х0) производная…

Общая схема исследования функций и построения их графиков. Пример.

Общая схема исследования функций и построение их графиков. Пример.

1. область определения. Точки разрыва.

2. если есть точки разрыва, то находим ВА

3. исследуем поведение функций при x→∞, т.е. находим ГА

4. y’. y’=0, схема знаков производных между критическими точками, устанавливаем точки экстремума

5. точки пересечения гр.функций с осями 0х и 0у

6. исследование на четность/нечетность функции

Исследовать и построить график

1. d (у)= (-∞ж+∞) 2. е 2х - х2= е-х2 = е-∞=0 d =0- ГА 3. у’= (е 2х - х2)’= е 2х - х2*(2-2х)

Дифференциал функции и его геометрический смысл. Инвариантность формы дифференциала 1-го порядка.

Опр. Дифференциалом фун-и наз-ся главная, линейная относительно дельта х часть приращения фун-и, равная произведению производной на приращение независимой переменной.

Геометр.смысл диф-ла. Диф-л фун-и есть приращение ординаты касательной, проведенной к графику фун-и y=f(x) в данной точке, когда х получает приращение дельта х.

Dy=f’(u) du – это сво-во диф-ла получило название инвариантности формы диф-ла.

 

Понятие первообразной функции. Неопределенный интеграл и его свойства (одно из свойств доказать).

Функция F(x) называется первообразной функцией для функции f(x) на промежутке х, если на всех точках этого промежутка, выполняется равенство:

F’(x)=f(x)

Совокупность всех первообразных F(x)+C для функции y=f(x) называется неопределенным интегралом от функции y=f(x)

⌠f(x)dx=F(x) +C

Свойства неопределенного интеграла

1.(f(x)dx)’=f(x)

Док-во

(⌠f(x)dx)’=(F(x)+C)’=F’(x)+C’=f(x)

2.d(⌠f(x)dx)’=f(x)dx дифференциал от неопределенного интеграла равен подынтегральному выр-ю

3.⌠dF=F+C интеграл от диф-ла функции равен самой функции с точностью до константа

4.⌠са(ч)вч=с⌠а(ч)вч

5.⌠(а(ч)+-п(ч))вч= ⌠а(ч)вч+-⌠п(ч)вч

 

 

Метод замены переменной в неопределенном интеграле и особенности применения этого метода при вычислении определенного интеграла.

Метод замены переменной в неопределенном интеграле - ∫ f(x) dx = ∫ f(φ(t)) φ’ (t) dt;

Метод замены пер-ой в опр.интеграле - ^b∫_a f(x) dx = ^b∫_a f(φ(t)) φ’ dt.

 

Метод интегрирования по частям для случаев неопределенного и определенного интегралов (вывести формулу). Примеры.

Неопределенный интеграл

U=U(x) и V=V(x) Т.к. d(uv) = (uv)’dx=u’vdx+uv’dx= du*v+u*dv, то проинтегрируем по переменной х… ⌠d(uv)= ⌠vdu+⌠udv

Определенный интеграл.

^b⌠udv=(uv-⌠vdu)^b│

^{a a}

u=u(x), v=v(x)

^b⌠udv=uv^b│-⌠ ^b vdu

^{a a a}

Определенный интеграл как предел интегральной суммы. Свойства определенного интеграла.

Сво-ва опр.интеграла: 1. Постоянный множитель можно выносить за знак интеграла. 2. Интеграл от алгебраической суммы двух фун-ий равен такой же сумме интегралов от этих фун-ий.

Теорема о производной определенного интеграла по переменному верхнему пределу. Формула Ньютона—Лейбница.

Φ(x)= x⌠f(x)dx = x⌠f(t)dt a a  

Формула Ньютона-Лейбница.

Определенный интеграл в пределах от a и b от непрерывной функции равен приращению любой ее первообразной на отрезке [a;b].

^b⌠f(x)dx = F(b)-F(a)

^a

1.при x=a ^a⌠f(t)dt=F(a)+C

^a

F(a)+C→C= -F(a)

2.x=b

^b⌠f(t)dt=F(b)-F(a)

^a

Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона (без доказательства).

Опр. Несобственным интегралом ^+∞∫_а f(x) dx от фун-и f(x) на полуинтервале [a;+∞] наз-ся предел фун-и Ф(t) при t, стремящимся к +∞.

 

^+∞∫_-∞ e^-x2/2 dx – несобственный интеграл Эйлера-Пуассона.

Вычисление площадей плоских фигур с помощью определенного интеграла. Примеры.

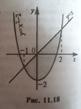
1.Пусть фун-я y=f(x) неотрицательна и непрерывна на отрезке [a,b]. Тогда по геометрич.смыслу определ.интеграла площадь S под кривой y=f(x) на [a,b] численно равна опред.интегралу, т.е. S = ^b∫_a f(x)dx. 2.Пусть фун-я y=f(x) неположительна и непрерывна на [a,b]. Тогда S = ^b∫_a (-f(x)) dx, т.е. S = - ^b∫_a f(x)dx. 3.Пусть на отрезке задана непрерывная фун-я общего вида. Тогда, S=S₁+S₂+S₃, т.е. равна алгебраич.сумме соответствующих опред.интегралов: S = ^c∫_a f(x)dx - ^d∫_c f(x)dx + ^b∫_d f(x)dx. 4.Тео-ма. Пусть на отрезке заданы непрерывные фун-и y=f₁(x) и y=f₂(x) такие, что f₂(x)> f₁(x). Тогда площадь S фигуры, заключенной между кривыми y=f₂(x) и y=f₁(x), на отрезке вычисляется по формуле: S = ^b∫_a (f₂(x) – f₁(x)) dx. При-р:Найти пло-дь фиг-ры, огранич.линиями y=x²-2, y=x.(рис.11.18).Реш-е: система: y=x²-2 и y=x => (-1;-1) и (2;2). На отр-ке [-1,2] x>x²-2. f₂(x)=x, f₁(x)=x²-2. S=²∫_-1 (x-(x²-2)) dx = x²/2 ²|_-1 – x³/3 ²|_-1 +2x ²|_-1 =1/2(4-(-1)²) – 1/3(2³-(-1)³) +2(2-(-1)) = 4,5 (ед.²).

 

Понятие о дифференциальном уравнении. Общее и частное решения. Задача Коши. Задача о построении математической модели демографического процесса.

Общим решением диф-ного урав-я n-ого порядка называется такое решение: y=φ (x, C1, ..., Cn), которое является фун-ей переменной x и n… Частным решением диф-ного урав-я наз-ся решение, получаемое из общего решения… Задачи Коши – это решения урав-я удовлетворяющих условию x0 y0 : y0=f(x0).

Простейшие дифференциальные уравнения 1-го порядка (разрешенные относительно производной, с разделяющимися переменными) и их решение. Примеры.

Рассмотрим вопросы теории диф-ных урав-й на примере урав-й первого порядка, разрешенных относительно производной, т.е. таких, кот.допускают представление в виде y’=f(x,y). Тео-ма. Пусть в диф-ном урав-и фун-я f(x,y) и ее частная производная дf/дy непрерывны на открытом множестве Г координатной плоскости Oxy. Тогда: 1)Для всякой точки (x₀,y₀) множества Г найдется реш-е y=y(x) урав-я, удовл-щее условию y₀=y(x₀); 2)Если два решения y=y₁(x) и y=y₂(x) урав-я совпадают хотя бы для одного значения x=x₀, т.е. если y₁(x₀)=y₂(x₀), то эти решения совпадают для всех тех значений переменной х, для которых они определены. Прим-рЖнэ=ню Реш-еЖ а(чбн) = нб да.дн=1ю н=Су^чю Пусть н=н(ч)ж н₀=н(ч₀)ж С=н₀у^-ч0ж н=н(ч) и н=Су^ч=н₀у^-ч0у^ч=н₀у^ч-ч0 – уравнения совпадают при ч=ч₀ю

Однородные и линейные дифференциальные уравнения 1-го порядка и их решения. Примеры.

Дифференциальное урав-е первого порядка наз-ся однородным, если оно может быть представлено в виде y’=g(y/x). Понятие однород-го диф-го урав-я связано с однород-ми фун-ми. Фун-я y=f(x,y) наз-ся однородной степени k (по переменным x и y), если для произвольного числа α выполняется равенство f(αx, αy)=α^k f(x,y) При-р: f(x,y)=x² – xy. f(αx, αy)=(αx)² – (αx)(αy)=α²(x² – xy)= α² f(x,y), данная фун-я однород-я степени 2.

Диф-ное урав-е первого порядка наз-ся линейным, если оно имеет вид y’+f(x)y=g(x). В случае, когда фун-я g(x) тождественно равна нулю, урав-е наз-ся однород-м, в противном случае – неоднород-м.

 

Определение числового ряда. Сходимость числового ряда. Необходимый признак сходимости рядов (доказать). Примеры.

Числовым рядомназывается бесконечная последовательность чисел, соединенных знаком сложения.

u₁+u₂+….u_n= ∑ u_n=Sсумма сходящегося ряда

Предел частной суммы Sn ряда (конечный или бесконечный) называется суммой ряда S=lim Sn

Пример

1.1-+1-1+1-1+1….

S₁=1; S₂=0; S3=1

Пределы частной суммы не сущ – ряд рас-ся

Сходимость числового ряда

Ряд называется сходящимся, если существует конечный предел последовательности, его частичных сумм, если конечного предела не сущ при n→∞, то ряд называется рас-ся

Необходимый признак сходимости.

lim Un=0 n→∞, lim Un=lim (Sn-Sn-1)= limSn-lim Sn-1= S-S=0

Гармонический ряд и его расходимость (доказать).

Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов. Абсолютная и условная сходимость рядов.

Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны.

Признак Лейбница

Ряд сх-ся , если выполнены 2 усл 1. члены ряда монотонно убывают по абсолютной величине., т.е an≥an+1

Абсолютно и условно сходящиеся ряды

Ряд называется условно сходящимся, если сам данный ряд сх-ся, а ряд, составленный из абсолютных величин его членов рас-ся. Св-ва абсолютно и условно сходящихся рядов существенно отличаются, так абс.… 1-1/2+1/3-1/4…. Условно сх-ся.