Понятие матрицы. Виды матрицы. Транспонирование матрицы. Равенство матриц. Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.

№1. а)Понятие матрицы. б)Виды матрицы. в)Транспонирование матрицы. г)Равенство матриц. д)Алгебраические операции над матрицами: умножение на число, сложение, умножение матриц.

а)Матрицей размера m×n наз прямоугольная таблица сост из m-строк и n-столбцов.

⌠а₁₁а₁₂а_13……а_1n ⌠

А= |a₂₁a₂₂a_33……a_2n |=(a_ij)_m×n=[a_ij]_m×n.

|……………… |

⌡a_m1a_m2a_m3…a_mn⌡

a_ij-элементы матрицы. i-номер строки j-номер столбца

б)Матрица сост из одной строки наз матрицей строкой(вектором строкой):В=(b₁₁b_12…b_1n).

Матрица сост из одного столбца наз матрицей-столбцом(вектором-столбцом).

[c₁₁]

C=| c₂₁ |

| … |

[c_m1]

Если кол-во строк = кол-ву столбцов, то матрица наз квадратной размера m×n (матрица порядка m). Диагональная матрица-матрица все элементы кот, кроме диагональных =0.

Элементы матрицы у кот номер столбца = номеру строки наз диагональными и образуют главную диагональ матрицы. Если у диагональной матрицы все диагональные элементы =1, то она наз единичной. (Е=(…)). Матрица любого размера называется нулевой если все ее элементы равны 0.

в)Транспонирование матрицы- переход от матрицы А к матрице А^/, в кот строки и столбцы поменялись местами с сохранением порядка. Матрица А^/ наз транспонированной относительно матрицы А. Св-ва: 1) (А^/)^/=А, 2) (λА^/)^/=λА^/, 3) (А+В)^/=А^/+В^/.4) (АВ)^/=А^/В^/.

г)Две матрицы А и В одного размера наз равными,если они совпадают поэлементно, т е a_ij=b_ij для любых i=1,2,…m; j= 1,2,…,n.

д)1. Умножение матрицы на число. Произведением матрицы А на число λ наз матрица В=λА, элементы кот b_ij=λa_ij для i=1,2,…,m; j=1,2,…,n. Общий множитель всех элементов матрицы можно выносить за знак матрицы. Произведение матрицы А на число 0, равно нулевой матрице. (0А=0).

2. сложение матриц. Суммой двух матриц А и В одинакового размера m×n наз матрица С=А+В, элементы кот c_ij=a_ij+b_ij для i=1,2,…,m; j=1,2,…,n. ( т е матрицы складываются поэлементно). В частности А+0=А.

3. Вычетание матриц. Разность двух матриц одинакового размера опред ч/з предыдущие операции А-В= А+(-1)В.

4. Умножение матриц. Умножение матрицы А на матрицу В определено, если число столбцов матрицы А равно числу строк матрицы В. Произведением матрицы А размера m×k на матрицу В размера k×n наз матрица С размера m×n, каждый элемент кот = сумме произведений элементов i-строки матрицы А на соответствующие элементы j-столбца матрицы В. c_ij=a_i1b_1j+a_i2b_2j+…+a_ikb_ik.

№2. а)Определители 2-го,3-го и п-го порядков (определения и из св-ва). б)Теорема Лапласа о разложении определителя по элементам строки или столбца.

а) Определителем матрицы 2-го порядка наз число, кот вычисляется по формуле:

∆₂=|А|=|а₁₁а₁₂|=а₁₁а₂₂-а₁₂а_21.-члены определителя.

|а₂₁а₂₂ |

Определителем матрицы 3-го порядка кот вычисляется по формуле: ∆₃=|А|=а₁₁а₂₂а₃₃+а₁₂а₂₃а₃₂+а₂₁а₃₂а₁₃-а₃₁а₂₂а₁₃-а₁₂а₂₁а₃₃-а₃₂а₂₃а₁₁.

Определителем квадратной матрицы n-го порядка наз число =алгебраической сумме п! членов, каждый из кот явл произведением п элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как (-1)^r(J)где r(J)-число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания: ∆=|А|=∑_(J)(-1)^r(J)a_1j1a_2j2…a_njn.

C-ва:1) если какая-либо строка (столбец) матрицы сост из одних нулей, то ее определитель=0. 2) если все элементы какой-либо строки (столбца) матрицы умножить на число λ, то ее определитель умножится на это число. 3) При транспонировании матрицы ее определитель не изменяется |A^/|=|A|. 4) при перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный. 5) если квадратная матрица содержит две одинаковые строки(столбца), то ее определитель=0. 6) если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0. 7) сумма произведений элементов какой-либо строки(столбца) матрицы на алгебраичские дополнения элементов др строки (столбца) этой матрицы равна 0. 8) определитель матрицы не изменится, если к элементам какой-либо строки(столбца) матрицы прибавить элементы др строки(столбца), предварительно умноженные на одно и тоже число. 9) Сумма произведений произвольных чисел на алгебраические дополнения элементов любой строки(столбца) = определителю матрицы, полученной из данной заменой элементов этой строки(столбца) на числа b₁,b₂,…,b_n. 10) определитель произведения двух квадратных матриц= произведению их определителей.

б)Определитель п-го порядка = сумме произведения элементов какой-либо строки или столбца на их алгебраические дополнения. ∆=а_i1A_i1+a_i2A_i2+…+a_inA_in. –разложение по строке. ∆=a_ijA_1j+a_2jA_2j+…+a_njA_nj- разложение по столбцу.

 

№3.а)Квадратная матрица и ее определитель. б)Особенная и неособенная квадратные матрицы. в)Присоединенная матрица. г)Матрица, обратная данной, и алгоритм ее вычисления.

а)Если кол-во строк= кол-ву столбцов, то такая матрица наз квадратной размером m×m(матрица порядка m). Понятие определитель приминяется только для квадратных матриц, detA,(А),∆. Определителем кв матрицы А наз число, кот вычисляется по след правилам: 1) А=(а₁₁) detA=а_11. 2) А=(а₁₁а₁₂) detA=а₁₁а₂₂-а₁₂а_21.

(а₂₁а₂₂)

3) А=(а₁₁а₁₂а₁₃)

(а₂₁а₂₂а₂₃)

(а₃₁а₃₂а₃₃)

Для 3) правилом ∆(Саррюса). detA=а₁₁а₂₂а₃₃+а₁₃а₂₁а₃₂+а₃₁а₁₂а₂₃-а₃₁а₂₂а₁₃-а₁₁а₃₂а₂₃-а₃₃а₂₁а_12.

4) Определитель п-го порядка – сумме произведения элементов какой-либо строки или столбца на их алгебраические дополнения. ∆=а_i1A_i1+a_i2A_i2+…+a_inA_in. –разложение по строке. ∆=a_ijA_1j+a_2jA_2j+…+a_njA_nj- разложение по столбцу.А_ij=(-1)^i+jM_ij- алгеброическое дополнение.

в,г)Пусть матрица А- кв. Матрица А^-1-наз обратной к матрице А, если выполняется усл: А^-1А=АА^-1=Е. Мариица наз невыражденной, если ее определитель не =0, в противнос случае матрица-выражденная. Теорема(необходимое и достаточное усл сущ обратной матрицы):Обратная матрица А^-1сущ единственно тогда и только тогда, когда исходная матрица невыражденная и вычисляется по формуле А^-1= 1/ detA×А^~, А^~-присоединенная матрица сост из алгебраических дополнений транспонированной матрицы

А^~= (А₁₁А₂₁…А_п1/А₁₂А₂₂…А_п2/…/А_1пА_2п…А_пп). Схема вычисления обр матрицы:

1) вычисляем определитель матрицы. Если определитель равен нулю , то матрица вырожденная и обратной матрицы не сущ. Если detA не=0, то: 2) вычисляем алгебраические дополнения и составляем присоединенную матрицу А^~. 3) Составляем обратную матрицу по формуле: А^-1= 1/ detA×А^~. 4) Выполняем проверку: А^-1А=Е.

 

№4. а)Понятие минора к-го порядка. б)Ранг матрицы(определение).в)Вычисление ранга матрицы с помощию элементарных преодразований.Пример.

а)В матрице А размера т×п вычеркиванием каких-либо строк и столбцов можно вычленить квадратные подматрицы к-го порядка, где к<=min(m;n). Определители таких подматриц наз минорами к-го порядка матрицы А.

б)Рангом матрицы А наз наивысший порядок отличных от 0 миноров этой матрицы.

в)Элементарные преобразования: 1) отбрасывание нулевой строки(столбца). 2) Умножение всех элементов строки (столбца) матрицы на число, не равное 0. 3) Изменение порядка строк (столбцов) матрицы. 4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов др строки (столбца), умноженных на любое число. 5) Транспонирование матрицы.

Пример. (0 -1 3 0 2)

А= (2 -4 1 5 3)= (2 -4 1 5 3)

(-4 5 7 -10 0) (0 -1 3 0 2).

(-2 1 8 -5 3)

r(A)=2. Матрица имеет ступенчатый вид и содержит миноры 2-го порядка, не =0, например |2 -4|

|0 -1|=-2 не=0.

 

№5. а)Линейная независимость столбцов (строк) матрицы. б)Теорема о ранге матрицы.

а)Если линейная комбинация строк λ₁е₁+ λ₂е₂+… +λ_ме_м=0, тогда и только тогда, когда все коэффициенты λ_i =0, т е λ₁=λ₂=…= λ_м=0,то строки е_1,е₂,…,е_т наз линейно независимыми. λ-число, е₁=а₁₁а₁₂а₁₃…_, е₂=а₂₁а₂₂а_23.

б)Ранг матрицы = максимальному числу ее линейно независимых строк или столбцов, ч/з кот линейно выражаются все остальные ее строки (столбцы).

 

6. Векторы. Операции над векторами (сложение, вычитание, умножение на число), n-мерный вектор. Понятие о векторном пространстве и его базисе.

Геом.вектор. Вектор АВ^-> – направленный отрезок прямой (АВ) с нач.в т.А и концом в т.В. При умнож.вектора на число «У» получается коллинеарный в-р.

Длина в-ров |АВ|= кв.корень х²+у²

В-ры,лежащие на одной прямой наз-ся коллинеарными. В-ры,лежащие в одной плоскости или ||-ных плоскостях наз-ся компланарными. Если нач.и конец вектора совп.,то в-р наз-ют нулевым. Длина нул.вект.=0.

Вектором,противоп-м в-ру а^->,наз-ся произвед.в-ра а^->на ч-ло (-1),т.е. - а^->=(-1)а^->.

Координатами в-ра а^-> наз-ся корд-ты его конечной точки. На плоскости Oxy два ч-ла - (х;у), в пространстве Oxyz три ч-ла - (х;у;z).

В-р а^-> = (x;y;z) мож.б.записан в виде а^-> = хi^-> +yj^->+zk^->. i^->,j^->,k^-> – единичные в-ры(орты),совпадающие с направл.соотв.осей Ох,Оу,Оz. хi^->,уj^->,zk^-> - компоненты в-ра.

Операции над в-ми:

1) Суммой двух в-ров а^-> и b^-> наз-ся в-р с^->=а^->+ b^->,нач.кот.совп-т с нач.в-ра а^->, а конец – с концом в-ра b^->при усл.,что нач.в-ра b^-> совп.с концом в-ра а^->.

Правило треугольника. Для слож.2-х в-ров а^->и b^-> по правилу треуг-ка оба эти в-ра переносятся ||-но самим себе так,чтобы нач.одного из них совп.с концом другого. Тогда в-р суммы задаётся 3-ей стороной образовавшегося треуг-ка, причём его нач.совп.с нач.первого в-ра.

2)умнож.в-ра на ч-ло:при умнож.в-ра на ч-ло Y пол-ся коллинеарный в-р. (Произвед.в-ра а^-> на ч-ло У наз-ся в-р b^->=Уа^->,имеющий длину |b^->|=|У||а^->|,направление кот.совп.с направл.в-ра а^->, если У<0.) Если b^->= а^->Y,то а^->|| b^->. И наоб.,если а^->|| b^->( а^->не=0),то b^->= а^->Y.

3) Разностью 2-х в-ров а^->и b^-> наз-ся сумма в-ра а^-> и в-ра -b^->,противоположного b^->.

||Скалярным произведением 2-х в-ров наз-ся ч-ло,равное произведению длин этих в-ров на косинус угла между ними: а^-> * b^-> *cosф, где ф-угол между в-рами а^-> и b^->. В-ры явл-ся ||-ми тогда и только тогда, когда их скал.произвед.=0.

||n-мерным в-ром наз-ся упорядоченная совокуп.n действительных чисел,записываемых в виде х=(х₁,х₂,..,х_n),где числа х₁,х₂,х₃,..х_n компоненты в-ра.

Равенство в-ров.Векторы х и y равны тогда и только тогда, когда равны их соотв.компоненты,т.е. х=у,если х_i=у_j, i=1,2,…,n.

Суммой 2-х в-ров одинак.размерности n наз-ся в-р z=x+y,компоненты кот.равны сумме соотв.компонент слагаемых в-ров,т.е.z_i=x_i+y_i,i=1,2,...,n.

Произв-м в-ра на действит.ч-ло Y наз-ся в-р u=Yx,комп-ты кот.равны произв-ю Y на соотв.комп-ты в-ра х,т.е. u_i = Yx_i, i=1,2,...,n.

Линейные оп-ции над люб.в-рами удовлет.след.св-вам: 1)х+у=у+х – коммутативное, 2)(х+у)+z=х+(у+z) – ассоциативное(сочетательное), 3)альфа(бета*х)=(альфа*бета)х, 4)альфа(х+у)=альфа*х+альфа*у, 5)(альфа*бета)х=альфа*х+бета*х, 6)сущ-т нул.в-р 0=(0,0,…,0)такой,что х+0=х для люб.в-ра х., 7)для люб.в-ра сущ-т противоп.в-р (-х) такой,что х+(-х)=0., 8)1*х=х для люб.в-ра х.

Опр.:ВЕКТОРНОЕ ПР-ВО:множество в-ров с действит.компонентами,в котором определены операции сложения в-ров и умнож.в-ра на ч-ло,удовлетворяющее приведённым выше 8-ми св-вам.

n-векторное пространство – это множество всех n-мерных векторов.

Вектор а_m наз-ся линейной комб-ей в-ров а₁,а₂,..,а_m в-рного простр-ва R,если он равен сумме произв-ний этих в-ров на произвол.действит.ч-ла: am= Y₁a₁+ Y₂a₂+ ...+Y_m-1a_m-1, где Y₁,Y₂,...,Y_m-1 – какие угодно действит.ч-ла.

Опр.:В-ры а₁,а₂,…,а_m в-рного простр-ва R наз-ся лин.завис.,если сущ-ют такие ч-ла Y1,Y2,...,Ym,не равные одновременно нулю, что Y₁a₁+Y₂a₂+...+ Y_ma_m=0. В противном случае в-ры наз-ют лин.независ.

Лин.простр-во наз.n-мерным,если в нём сущ-ет n линейно независ.в-ров,а любые из (n+1) в-ров уже явл-ся завис. Размерность пр-ва – это максимально ч-ло содержащихся в нём линейно независ.в-ров. Ч-ло n наз-ся размерностью пр-ва R. Совокупность n линейно независ.в-ров n-мерного пр-ва таких,что любой в-р прост-ва может быть единственным образом представлен в виде их лин.комбинации наз-ся БАЗИСОМ.

Если е₁,е₂,…,е_n – система лин.независ.в-ров пр-ва R и любой в-р а лин.выражается через е₁,е₂,…,е_n, то пр-во R явл-ся n-мерным,а в-ры е₁,е₂,…,е_n – его базисом.

 

7. Собственные векторы и собственные значения матрицы. Характеристическое уравнение матрицы.

Опр:В-р Х наз-ся собственным в-ром квадр.м-цы А, если он не нулевой и удовлетворяет ур-еА_nx1* Х_nx1=Y_* X_nx1,где Y-собств.зн-е квадр.м-цы А.коллинеарный в-р.

Число Y наз-ся собственным зн-ем оператора А^~ (м-цы А),соответствующим в-ру Х.

Метод вычисления собств.зн-ий и собств.в-ров.Т.к. Х_nx1=Е_{nx1 *} Х_nx1, то АХ=YEX ~ AX-YEX=0 ~ (A-YE)X=0. Если _^ = |A-YE|=0,то т.к.все _^1=0, сист.ур-ий имеет бескон.много реш.в этом сл-е (0/0).

Ур-е |A-YE|=0 – характеристическое ур-е м-цы. Из него находим Y и далее по ур-нию (A-YE)X=0 находим соотв.ненул.в-р Х.

Св-ва собств.зн-ний м-цы А: 1)Произвед-е собств-х зн-ний м-цы А равно её определителю |А|=Y1,Y2,...,Yn.

2)Число отличных от нуля собств.зн-ний м-цы А = её рангу.

3)Все собств.зн-я м-цы отличны от 0 тогда и только тогда,когда м-ца А невырожд.

4)Если Yне=0 – собств.зн-е невырожд.м-цы А,то Y-1=1/Y – собств.зн-е обрат.м-цы А^-1. 5)Если Y – собств.зн-е м-цы А,то Y^m-собств.зн-е м-цы А^m, где m – натур.ч-ло.

 

8. Система п линейных уравнений с п переменными (общий вид). Матричная форма записи такой системы. Решение системы (определение). Совместные и несовместные, определенные и неопределенные системы линейных уравнений.

8. Система лин.ур-ний:

А_mxn*Х_nx1=В_mx1 <=> (ф.1)

(a₁₁x₁+a₁₂x₂+…+ а_nx_n=b₁

(a₂₁x₁+a₂₁x₂+… +a_2nx_n=b₂

(….

(а_mx₁+а_2mx₂+… +а_mnх_n=b_m

Вматричной формесистема имеет вид АХ=В, где

(а₁₁ a₁₂ ... a_1n)

A= (a₂₁ a₂₂ ... a_2n)

ф.2(... ... ... ... );

(a_m1 a_m2 .. a_mn)

(x₁)

X= (x₂)

ф.3 (....);

(x_n)

(b₁)

B= (b₂)

ф.4(....);

(b_m)

называются собственно матрицей системы, матрицами-столбцами переменных и свободных членов.

Решение системы:а)методом обр.м-цы. Ур-е в матричной ф-ме имеет вид АХ+В. Найти обр.м-цу. И найдём Х по ф-ле Х=А^-1В,(т.е.х₁,х₂,х₃.)

Б)По ф-ле Крамера. Найти определитель системы ^=|A|. Если он не=0,то сист.имеет единств.реш. Далее вычислить опред-ли м-ц ^1,^2,^3,полученных их м-цы А,заменой соотв-но 1-го,2-го и 3-го ст-цов столбцом своб.членов. Далее по ф-лам Крамера:х1=^1/^,х2=^2/^, х3=^3/^.

Расширенной м-цей системы наз.м-ца (А|В),полученная из м-цы сист.А добавлением к ней ст-ца членов этой системы,т.е. (А|В)=(ф.2|ф.4)

Теорема Кронекера-Капелли.Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы.

r<m – ур-я с-мы(строки расш.м-цы)зависимые;

r=m –ур-я с-мы (стр.расш.м.)независимые;

r(A)не=r(A|B)- с-ма несовм-ная;

r(A)=r(A|B)=r – с-ма совм-ная;

r<n – с-ма неопред.(бескон.мн.реш.);

r=n – с-ма опред-ная (единств.реш.)

Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.

Если система лин.ур-й имеет единств.решение Х=(х₁,х₂,…х_n),то такая сист.наз.определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист.не определённая.

 

9. Метод Гаусса решения системы n линейных уравнений с п переменными. Понятие о методе Жордана – Гаусса.

Метод Гаусса –метод послед-го исключ.переменных.

Сначала(на 1-м шаге прямого хода Гаусса) из всех ур-ний,кроме 1-го исключается переменная х₁. Потом (на 2 шаге) из всех ур-й,кроме первых 2-х исключается переменная х₂ и т.д.,пока последнее ур-е не приобретёт вид:С _* Х_n=b_m,если ч-ло С=0, а b_m не=0,то с-ма не совместная,т.е.нет решений. Если С=0 и b_m=0,т.е. 0_*Х_n=0,то с-ма неопределённая,т.е. имеет бескон.мн.реш.,то с-ма совместно-определённая. В этом сл-е Хn=b_n/C

Полученное зн-е Х_n подстав.в предпосл.ур-е,находим Х_n-1и тд.,пока не получ.все неизв-е.

Обратный ход Гаусса. Из м-цы ступенч.вида записывается ур-е. Далее,начиная с конца находим все переменные. Допустим Х₄. Подставляем в верхнее и нах-м Х₃ и т.д.

Метод Гаусса — Жордана исп-ся для реш.квадр.систем лин.ур-ний, нахождения обрат.м-цы, отыскания ранга м-цы. Метод явл-ся модификацией метода Гаусса. Назван в честь Гаусса и Жордана.

Теорема Кронекера-Капелли.Сист.лин.ур-й совмест.тог.и т.тог,ког.ранг м-цы сист.А равен рангу расшир.м-цы (А|B) этой с-мы.

r<m – ур-я с-мы(строки расш.м-цы)зависимые;

r=m –ур-я с-мы (стр.расш.м.)независимые;

r(A)не=r(A|B)- с-ма несовм-ная;

r(A)=r(A|B)=r – с-ма совм-ная;

r<n – с-ма неопред.(бескон.мн.реш.);

r=n – с-ма опред-ная (единств.реш.)

Если у сист.ур-ния есть реш-е,то такая система совместна,если решения ур-я нет, то не совместная.

Если система лин.ур-й имеет единств.решение Х=(х₁,х₂,…х_n),то такая сист.наз.определённой. Если СЛУ имеет больше, чем одно реш-е,то такая сист.не определённая.

 

10. Системой m линейных уравнений с n неизвестными называется система вида

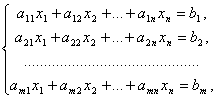
где a_ij и b_i (i=1,…,m; b=1,…,n) – некоторые известные числа, а x₁,…,x_n – неизвестные. В обозначении коэффициентов a_ij первый индекс iобозначает номер уравнения, а второй j – номер неизвестного, при котором стоит этот коэффициент.

Коэффициенты при неизвестных будем записывать в виде матрицы 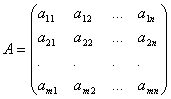, которую назовём матрицей системы.

Числа, стоящие в правых частях уравнений, b₁,…,b_m называются свободными членами.

Совокупность n чисел c₁,…,c_n называется решением данной системы, если каждое уравнение системы обращается в равенство после подстановки в него чисел c₁,…,c_n вместо соответствующих неизвестных x₁,…,x_n.

Теорема Кронекера-Капелли

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём…   12. Решение систем линейных алгебраических уравнений общего вида.

Приведение квадратичных форм к каноническому виду

Это симметрическое преобразование можно записать в виде: y1 = a11x1 + a12x2 y2 = a12x1 + a22x2

Каноническое уравнение эллипса.

. (4) Доказательство. Доказательство проведем в два этапа. На первом этапе мы… Геометрический смысл параметра - расстояние от начала координат до плоскости. Вектор нормали направлен в сторону…

Условия параллельности и перпендикулярности плоскостей.

.   Плоскости параллельны, векторы нормалей коллинеарны: ïï.Это условие выполняется, если: .

Условия параллельности и перпендикулярности прямых в пространстве

Чтобы две прямые были перпендикулярны необходимо и достаточно, чтобы направляющие векторы этих прямых были перпендикулярны, т.е. косинус угла между…   32. Угол между двумя плоскостями равен углу между их нормальными векторами. Пусть две пересекающиеся плоскости A1x +…

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость

.   Плоскости параллельны, векторы нормалей коллинеарны: ïï.Это условие выполняется, если: .

Условия параллельности и перпендикулярности прямой и плоскости в пространстве

Для того, чтобы прямая и плоскость были перпендикулярны, необходимо и достаточно, чтобы вектор нормали к плоскости и направляющий вектор прямой были…