Однородная система линейных уравнений.
Однородная система линейных уравнений AX = 0 всегда совместна. Она имеет нетривиальные (ненулевые) решения, если r = rankA < n.
Для однородных систем базисные переменные (коэффициенты при которых образуют базисный минор) выражаются через свободные переменные соотношениями вида:

Тогда n - r линейно независимыми вектор-решениями будут:
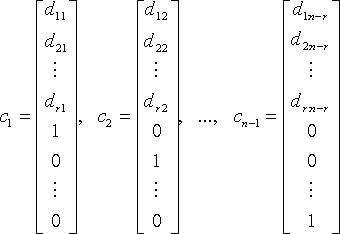
а любое другое решение является их линейной комбинацией. Вектор-решения 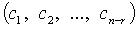 образуют нормированную фундаментальную систему.
образуют нормированную фундаментальную систему.
В линейном пространстве  множество решений однородной системы линейных уравнений образует подпространство размерности n - r;
множество решений однородной системы линейных уравнений образует подпространство размерности n - r; 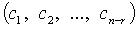 - базис этого подпространства.
- базис этого подпространства.
6)продолжение.Введем для системы линейных уравнений (1) следующие матрицы:
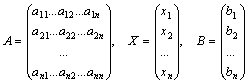 .
.
Систему (1) представим в матричной форме А* Х = В, которая эквивалентна исходной. Действительно, если перемножить матрицы А и Х и приравнять элементы матрицы-произведения к соответствующим элементам матрицы В, то получим систему уравнений (1).
Умножим обе части уравнения А*Х = В слева на матрицу А-1, получим А-1 * (А Х) = А-1 В или (А-1 А) Х= А-1 В.
Так как А-1 * А = Е, то Е*Х = А-1 * В или Х = А-1* В.
Эта формула дает решение системы в матричной форме.
Пример. Решить систему
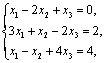 используя обратную матрицу.
используя обратную матрицу.
Решение. Найдем обратную матрицу к матрице системы  .
.
Определитель матрицы А: 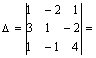
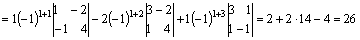 .
.
Так как определитель матрицы А отличен от 0, то обратная матрица существует. Найдем ее по формуле  , вычислив предварительно алгебраические дополнения. Получим:
, вычислив предварительно алгебраические дополнения. Получим:
 .
.
Найдем матричное решение системы:
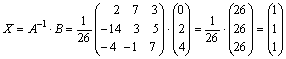 .
.
Ответ: х1 = 1; х2 = 1; х3 = 1.
7) продолжение.В другой форме правило Крамера формулируется так: для любых коэффициентов c1, c2, …, cn справедливо равенство:
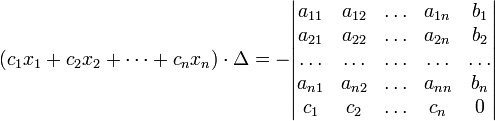
В этой форме формула Крамера справедлива без предположения, что  отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы
отлично от нуля, не нужно даже, чтобы коэффициенты системы были бы элементами целостного кольца (определитель системы может быть даже делителем нуля в кольце коэффициентов). Можно также считать, что либо наборы 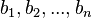 и
и 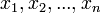 , либо набор
, либо набор 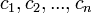 состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом.
состоят не из элементов кольца коэффициентов системы, а какого-нибудь модуля над этим кольцом.