Формула интегрирования по частям имеет вид

 

1 При нахождении интегралов вида

 

 

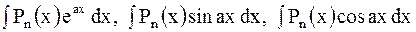
принимаем 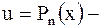многочлен степени ,

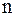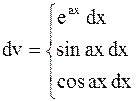
2 При нахождении интегралов вида

 

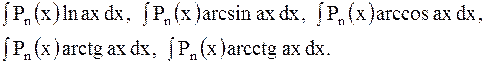
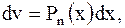
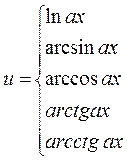
3 Интегралы, в которых двукратное применение формулы интегрирования по частям приводит к исходному интегралу

 

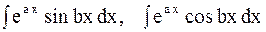
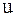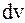Выбор и в таких интегралах произволен.

Простейшими дробями I, II, III, IV типов называются правильные рациональные дроби следующего вида:

I. ;

II. 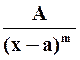, где m – целое число, большее единицы;

III. , где 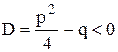, т.е. квадратный трехчлен 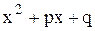не имеет действительных корней;

IV. , где n – целое число, большее единицы, и квадратный трехчлен 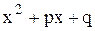не имеет действительных корней.

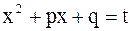Дроби I и II типов интегрируются с помощью подстановки t=x-a .для нахождения интеграла нужно в числителе дроби выделить производную знаменателя и разложить полученный интеграл на сумму двух интегралов: тогда первый из них подстановкой приведется к виду , а второй выделением полного квадрата в знаменателе – к виду .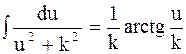

Для интегрирования простейшей дроби IV типа в числителе дроби нужно записать производную квадратного трехчлена и разложить полученный интеграл на сумму двух интегралов. Первый из них подстановкой 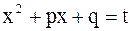приведется к виду , а второй имеет вид 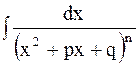. С помощью подстановки 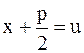он преобразуется в интеграл вида 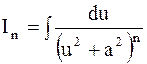, который интегрированием по частям можно свести к более простому интегралу 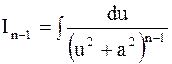того же типа, но показатель в знаменателе уменьшается на единицу. При этом справедлива следующая рекуррентная формула:

 

 

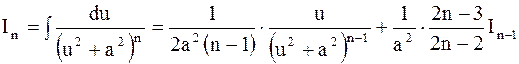
При большом n целесообразно применять эту формулу. Повторяя процесс (n-1) – раз, получим табличный интеграл 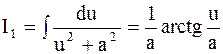.