Лекция 4. СОБЫТИЕ И ВЕРОЯТНОСТЬ

Лекция 4. СОБЫТИЕ И ВЕРОЯТНОСТЬ

План: 1.Основные понятия. Определение вероятности 2. Свойства вероятности

Свойства вероятности

 

Теорема сложения вероятностей несовместимых событий.

Пример 8.21. Испытание — стрельба двух стрелков (каждый делает по одному выстрелу). Событие А — попадание в мишень первым стрелком, событие В —… Аналогично суммой конечного числа событий А1, А2,,..., Аk называют событие… Определение 2. Произведением событий А и В называют событие С = =АВ, состоящее в том, что в результате испытания…

Формула полной вероятности.

(8.8) (формула полной вероятности).

Формула Бейеса.

Найдем условную вероятность РA(Вk). По теореме умножения вероятностей и формуле (8.5) (см. п. 2) имеем Р(AВk)= Р(A) РA (Вk)= . Отсюда

Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Дайте определения противоположным, независимым, несовместным событиям. Приведите примеры таких событий. 2. Что называется полной группой событий? 3. Сформулируйте теоремы сложения и умножения вероятностей.

Случайные величины

Определение 1. Случайной величиной называют переменную величину, которая в зависимости от исхода испытания случайно принимает одно значение из… Пример 9.1.1) Число очков, выпавших при однократном бросании игральной кости,… 2) прирост массы домашнего животного за месяц есть случайная величина, которая может принять значение из некоторого…

Математическое ожидание дискретной случайной величины

Пусть некоторая дискретная случайная величина X с конечным числом своих значений задана законом распределения: xi х1 х2 … Определение. Математическим ожиданием М(Х) дискретной случайной величины X… М(Х) = х1р1+х2р2 + ... +хn р n. (9.1)

Свойства математического ожидания дискретной случайной величины.

Постоянную С можно рассматривать как дискретную случайную величину, принимающую лишь одно значение С с вероятностью р = 1. Поэтому M(С) = С 1 = =С. 2. Постоянный множитель можно выносить за знак математического ожидания, т. е. М(СХ) = С М(Х).

Дисперсия дискретной случайной величины

  Y -100 р 0,3 0,4 0,3   Несмотря на то что математические ожидания величин X и Y одинаковы: М(Х)=М(Y)=0, возможные значения величин Х и Y…

Среднее квадратическое отклонение.

s(X) = . Введение среднего квадратического отклонения объясняется тем, что дисперсия… Пример 9.7. Случайная величина X — число очков, выпавших при однократном бросании игральной кости. Определим s(X).

Понятие о моментах распределения.

nk=M(Xk) Следовательно, если X имеет распределение X х1 х2 … то М(Х) = хk1р1+хk2р2 + ... +хkn р n..

Непрерывные случайные величины

Р(х) = Р(Х < х). Определение. Интегральной функцией распределения (или кратко функцией… F(х) = Р(Х < х). (9.4)

Математическое ожидание и дисперсия непрерывной случайной величины.

М(Х)= . Определение 2. Дисперсией непрерывной случайной величины X, математическое… D(Х)= .

Некоторые законы распределения случайных величин

Найдем вероятность того, что при п испытаниях событие А наступит т раз (m£п). Пусть событие А наступило в первых т испытаниях т раз и не наступило во всех… Общее число сложных событий, в которых событие А наступает т раз, равно числу сочетаний из п элементов по т элементов.…

Локальная и интегральная предельные теоремы Лапласа.

Локальная предельная теорема Лапласа (доказательство см. в [4]). Пусть р = Р(А) — вероятность события А, причем 0<р<1. Тогда вероятность того,… где q= 1-p, . Для функции j(x) имеется таблица (см. приложение 1) ее значений для положительных значений х (функция j(x) четная). …

Гипергеометрическое распределение

Для гипергеометрического распределения вероятность принятия случайной величиной Y значения y имеет вид , где D— число объектов, обладающих признаком A, в рассматриваемой совокупности объёма N. При этом y принимает значения…

Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Дайте определение случайной величины.

2.Напишите формулы для математического ожидания и дисперсии дискретной и непрерывной случайных величин.

3. Дайте определение локальной интегральной предельная теорем Лапласа

4. Напишите формулы, задающие биномиальное распределение, гипергеометрическое распределение, распределение Пуассона, равномерное распределение и нормальное распределение.

 

Лекция 6. Элементы математической статистики

Цель: Изучить основные понятия математической статистики

План:

1. Генеральная совокупность и выборка

2. Статистическое распределение выборки. Полигон. Гистограмма.

3. Оценки параметров генеральной совокупности по ее выборке

4. Генеральная и выборочная средние. Методы их расчета.

5. Генеральная и выборочная дисперсии.

6. Вопросы для контроля знаний и подведения итога прочитанной лекции

 

Генеральная совокупность и выборка

1. Генеральная совокупность и выборка.Пусть требуется изучить множество однородных объектов (это множество называется статистической совокупностью)… Лучше всего произвести сплошное обследование, т.е. изучить каждый объект.… Если сплошное обследование невозможно, то из всей совокупности выбирают для изучения часть объектов.

Оценки параметров генеральной совокупности по ее выборке

Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки… Обычно в распоряжении исследователя имеются лишь данные выборки генеральной… Опытные значения признака X можно рассматривать и как значения разных случайных величин Х1, Х2,..., Хn с тем же…

Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Что такое генеральная совокупность и выборка?

2. Дайте статистическое распределение выборки.

3. Как строятся полигон и гистограмма?

4. Какие методы расчета есть для генеральной и выборочной средних?

5. Как оценивают генеральную и выборочную дисперсии?

6. Какие оценки параметра называются состоятельными, несмещенными и эффективными?

 

Лекция 7. ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ. ОСНОВНЫЕ ПОНЯТИЯ

План: 1. Основные понятия и определения графа и его элементов 2. Деревья. Лес. Бинарные деревья

Основные понятия и определения графа и его элементов

Так о великих вещах помогают составить понятье

Малые вещи, пути намечая для их постижения.

Лукреций

Впервые понятие «граф» ввел в 1936 г. венгерский математик Денни Кёниг. Но первая работа по теории графов принадлежала ;«перу великого Леонарда Эйлера и была написана еще в 1736 г. с помощью графов изображаются схемы различных дорог, линии воздушных сообщений, газопроводов, теплотрасс, электросетей, а также микросхемы, дискретные многошаговые процессы, системы различных бинарных отношений, химические структурные формулы и другие диаграммы и схемы. Применяются графы для решения задач химии, экономики, электротехники и автоматики. 'Также они широко используются в информатике и строительстве. Без графов сложно анализировать классификации в различных науках.

ГрафомG = (V, X) называется пара двух конечных множеств: множество точек и множество линий X, соединяющих некоторые пары точек. В терминах декартова произведения (подразд. 1.5) подмножество множества V´V: XÌV´V.

 

 

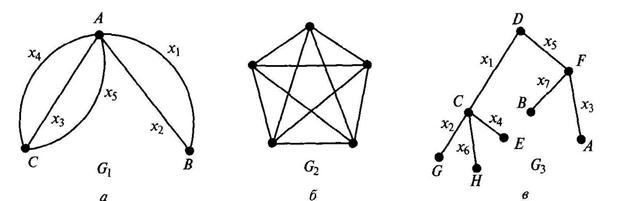
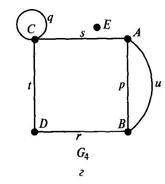
Рис. 2.1. Примеры графов: а — со смежными вершинами; 6 — полный; в – со смежными ребрами; г — с петлей

 

Точки называются вершинами или узламиграфа, линии — ребрамиграфа. Примеры графов приведены на рис. 2.1.

Пусть дан граф G = (V, X), где v = [V, W, ...} — конечное непустое множество его вершин, а Х(V, W) — его ребра. Если ребро графа G соединяет две его вершины V и W (т.е. <V, W>ÎX), то говорят, что это ребро им инцидентно.Две вершины графа называются смежными,если существует инцидентное им ребро: на рис. 2.1, а смежными являются вершины А и В, А и С. Если граф G имеет ребро Х(V, W), у которого начало и конец совпадают, то это ребро называется петлей.На рис. 2.1, г петля — q(С, С). Два ребра называются смежными,если они имеют общую вершину. На рис. 2.1, в смежными являются, например, ребра х₁ и х₂ с общей вершиной С.

Граф G( V, X) может иметь ребра с одинаковыми парами вида Х(V, W). Такие ребра называются кратными, или параллельными.На рис. 2.1, а кратными являются, например, ребра х₁(А, В), х₂(А, В). Вершинам А и В инцидентны ребра х₁ х₂, х₃. Количество одинаковых пар вида Х(V, W) называется кратностьюребра (V, W). На рис. 2.1, а ребро АС имеет кратность, равную 3, а ребро АВ — кратность, равную 2. Число ребер, инцидентных вершине А, называется степеньюэтой вершины и обозначается deg(A) (от англ. degree — степень). Если вершине инцидентна петля, она дает вклад в степень, равный двум, так как оба конца приходят в эту вершину.

На рис. 2.1, в вершина А имеет степень, равную 1, вершина С — 4, вершина D — 2. Записывается это в виде: deg (А) = 1, deg (С) = 4, deg (D) = 2. Граф G₄ (рис. 2.1, г) содержит пять вершин V= {А, В, С, , Е} и шесть ребер Х={p,q,r,s,t,u}.

Вершина графа, имеющая степень, равную нулю, называется изолированной.Граф, состоящий из изолированных вершин, называется нуль-графом.Для нуль-графа Х= Æ. Вершина графа, имеющая степень, равную 1, называется висячей.На рис. 2.1, г вершина Е — изолированная: deg(Е) = 0, а вершины А, В, Е, G,H на рис. 2.1, в — висячие.

Теорема 2.1.В графе G(V,Х) сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа:,

где п = ïVï — число вершин; т = ïХï — число ребер графа.

Вершина называется четной (нечетной ) если ее степень четное (нечетное) число.

На рис. 2.1, в deg (D) = 2, deg (F) = 3, значит, у графа G₃ вершина D является четной, а F — нечетной. В теории графов доказана следующая теорема.

Теорема2.2. Число нечетных вершин любого графа — четно.

Следствие. Невозможно начертить граф с нечетным числом нечетных вершин.

Граф G называется полным,если любые две его различные вершины соединены одним и только одним ребром. Полным является граф G₂ на рис. 2.1, б. Таким образом, полный граф определяется только своими вершинами. Пусть число вершин полного графа п. Тогда степень любой вершины, очевидно, равна deg (V) = п - 1, а число ребер равно числу сочетаний из п по 2, т. е. т =. Число ребер также можно найти по теореме 2.1: m=.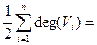

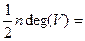
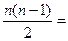
Дополнениемграфа G(V,Х)) называется граф (V, ) с теми же вершинами V, что и граф G, и имеющий те и только те ребра , которые необходимо добавить к графу G, чтобы он стал полным. Очевидно, что граф с кратными ребрами не имеет дополнения. Например, дополнением графа G₅ до графа G₂ на рис. 2.1, б является граф (рис. 2.2).

Как отмечалось в подразд. 1.3, дополнением универсального множества является пустое, и наоборот. Поскольку граф и его дополнение отличаются только ребрами (множества Х, ) и дополнение графов сводится к дополнению множества X , то частным случаем этого свойства будет следующее правило: дополнением полного графа будет нуль-граф, и наоборот.

Рис. 2.2. Дополнение G5 графа G5 до графа G2, изображенного на рис. 2.1, б	Рис. 2.3. Ориентированный граф

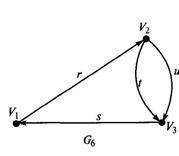
Если все пары (V_i , V_j) во множестве X являются упорядоченными, т.е. кортежами длины 2, то граф называется ориентированным, орграфом,или направленным.Поскольку сразу может быть не известно, о каком графе идет речь, в этой главе мы будем употреблять круглые скобки для обозначения ребра вместо угловых, как это должно было быть для кортежей. В них будет помещаться соответствующая пара вершин. В таком случае ребра принято изображать стрелками (рис. 2.3). Началомребра называется вершина, указанная в кортеже первой, концом— вторая вершина этой пары (графически она указана стрелкой). Ребра ориентированного графа имеют определенные фиксированные начало и конец и называются дугами.Очевидно, дуги (V₁ , V₃) и (V₃ , V₁), если они обе существуют, различны: (V₁ , V₃) ¹ (V₃ , V₁).

Степенью-входа (выхода) вершины ориентированного графа называется число ребер, для которых эта вершина является концом (началом).

Степень входа вершины V будем обозначать deg ₊( V), а степень выхода - deg _( V)- На рис. 2.3 deg ₊( V₁) = 1, deg ₊( V₂) = 1, deg ₊( V₃) = = 2, deg _-( V₁) = 1, deg _-( V₂) = 2, deg _-( V₃) = 1.

Дуги орграфа называются кратными,если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления. Например, кратны дуги u(V₂ , V₃) и t(V₂ , V₃) на рис. 2.3.

Последовательность попарно инцидентных вершин V_{i1 ,} V_i2, ..., V _ik неориентированного графа, т.е. последовательность ребер неориентированного графа, в которой вторая вершина предыдущего ребра совпадает с первой вершиной следующего, называется маршрутом.Число ребер маршрута называется длиноймаршрута. Например, на рис. 2.1, в НСDFD — маршрут длиной 4. Обозначение: НСDFD = 4. Очевидно, что если V_{i1 ,} V_i2, ..., V _ikс — маршрут длины k- 1, то и V _ik, V _ik-1, …_, V_i2, V_i1 также будет являться маршрутом длины k- 1. Маршрут принято задавать как последовательность ребер, поскольку это более удобно при наличии кратных ребер. Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутымили циклом.В графе G₄ (рис. 2.1, г) (t,s,p,r), (u,s,p,) — циклы длиной 4, (r,t, q s,u) — цикл длиной 5, (t,s,u,r,t,s,p,r) — 8-цикл, (р,и) — 2-цикл, петля (q) — 1-цикл.

Расстояниеммежду двумя вершинами называется минимальная длина из всех возможных маршрутов между этими вершинами при условии, что существует хотя бы один такой маршрут. Обозначается как d( V₁,V₂) (от лат. distantio — расстояние) d( V₁,V₂) = min| V₁,…,V₂|.

Поскольку рассматриваются конечные графы, минимум можно найти всегда. Очевидно, что d( V₁,V₂) = d( V₂,V₁). Формально можно ввести расстояние d( V ^’,V ^’). = 0 между любой вершиной и ей же самой, что соответствует нулевому маршруту, у которого начало и конец в одной вершине.

В маршруте одно и то же ребро может встретиться несколько раз. Если ребро встретилось только один раз, то маршрут называется цепью.Например, в графе G₄ (рис. 2.1, г) (t,s, р) — 3-цепь. Если (x_{1 ,} x₂, ... x _k-1,, x _k) — k-цикл, то любая циклическая перестановка, например (_, x₂, ... x_k-1,, x _k , x₁), также будет k:-циклом, поскольку сведется лишь к выбору начальной вершины. Частным случаем этого утверждения будет следующее: если k-цикл (x_{1 ,} x₂, ... x _k-1,, x _k) является цепью, то для любой циклической подстановки sÎS_k последовательность (x_{s(1) ,,} x_s(2), ..., x _s(k)) также будет k-циклом и цепью.

В орграфе маршрут является ориентированным и называется путем.На путь сразу налагаются важные требования, являющиеся частью определения:

• направление каждой дуги должно совпадать с направлением пути;

• ни одно ребро пути не должно встречаться дважды.

Другими словами, путь— упорядоченная последовательность ребер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны. На рис. 2.3 (u,r,s,t) — 4-путь, (r, и) — 2-путь, (s, r, t, s) путем не является. Тогда циклв орграфе — путь, у которого совпадают начало и конец. На рис. 2.3 (r,s,t) и (и, s,r) — 3-циклы. Для циклов орграфа также справедлива теорема о циклических подстановках. Цепь, путь и цикл в графе называются простыми,если они проходят через любую из вершин не более одного раза. Неориентированный граф называется связным,если между любыми двумя его вершинами есть маршрут.Для связного графа ориентация дуг не обязательна. Так, граф G₂ (рис. 2.1, б) является связным, а граф G₄ (рис. 2.1, г) — несвязным.Также можно ввести понятие связности для вершин графа: две вершины называются связными,если существует маршрут между ними. Понятно, что связность между вершинами является бинарным отношением. Это отношение будет отношением эквивалентности. Действительно, отноше­ние связности обладает известными свойствами (см. подразд. 1.6), т. е. оно:

рефлективно — каждая вершина (включая изолированные) связна сама с собой;

симметрично — любой маршрут (V, ..., V") можно представить в обратном порядке: (V"', ..., V ');

транзитивно — если вершина V соединена с вершиной V ' маршрутом М₁(Х₁ ..., Х_р), а вершина V ' соединена с вершиной V '' маршрутом М₂(Х_{р +1}, ..., Х_п), то вершина V соединена с вершиной V" маршрутом М₃(Х₁ ..., Х_р, Х_р+1, ..., Х_n), в котором сначала идут все ребра маршрута М₁, а затем все ребра маршрута М₂.

Граф G можно разбить на непересекающиеся подмножества Х_i по признаку связности. Вершины одного множества являются связными между собой, а вершины различных множеств — несвязны. Тогда все подграфы V_i (классы эквивалентности) графа G называют связными компонентами, или компонентами связности.Связный граф имеет одну компоненту связности.

Доказано, что в конечном связном графе всегда можно построить ориентированный цикл, проходящий через каждое ребро по одному разу в двух направлениях. Такой цикл называют способом обхода всего графа и используют при решении многих прикладных задач. В частности, разработаны специальные алгоритмы обхода ребер графа, которые можно использовать при решении задач вида «поиска выхода из лабиринта». В лабиринте дорожки служат ребрами графа, а их разветвления, начало движения (вход) и конец (выход) — вершинами графа. Если вход и выход принадлежат одной компоненте связности, то такой лабиринт принципиально проходим, если разным — то непроходим. Во втором случае не поможет даже мифологическая «нить Ариадны».

Теорема2.3. Для того чтобы связный граф G являлся простым циклом, необходимо и достаточно, чтобы каждая его вершина имела степень, равную 2.

Ребро (V, W) связного графа G называется мостом,если после его удаления G станет несвязным и распадется на два связных графа G ' и G ". На рис. 2.4 мост (СЕ) разделил связный граф G₇ на два различных связных графа: G ' с вершинами (А,В, С,D) и G " с вершинами (Е, F, G,Н,I). Также мостом является ребро ЕС.

 

Рис. 2.4. Граф G₇ с мостами BC и CE

 

Теорема 2.4.Ребро графа является мостом тогда и только тогда, когда не принадлежит ни одному циклу.

Какие графы можно считать различными, а какие не различаются?

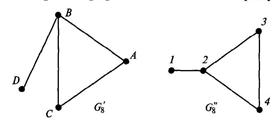
Графы G' и G" называются изоморфными,если существует взаимно-однозначное соответствие между их ребрами и вершинами, причем соответствующие ребра соединяют соответствующие вершины. Поскольку в данном издании исследуются конечные множества, такая биекция должна быть подстановкой. Между названием вершины и ее номером различия нет. Смежность двух вершин есть бинарное отношение, поэтому изоморфизм графов можно рассматривать как изоморфизм множеств их вершин (см. подразд. 1.4 и 1.6), на котором введено отношение смежности. Итак, графы G₁ (V₁ , Х₂) и G₂( V₂, Х₂) называются изоморфными,если | V₁| = |V₂| = п и существует подстановка sÎS_n, такая, что V₂ = s(V₁), а Х₂ = {s (V_i); s( V_j)) ï (V_i, V_j )Î Х₁}. Иными словами, можно так переобозначить; вершины первого графа, что в новых обозначениях вершины и ребра будут совпадать со вторым графом, причем кратным ребрам первого G '₈ должны соответствовать кратные ребра второго G ''₈ такой же кратности (рис. 2.5).

Аналогично устанавливается изоморфизм между ориентированными графами. При этом следует помнить, что ребро является упорядоченным множеством, и надо быть особенно внимательным, соблюдая порядок.

Важно, что изоморфизм графов является отношением эквивалентности. Это удобнее всего заметить исходя из свойств подстановок. На практике такие различные по внешним признакам изоморфные графы не различают, рассматривая их с точностью до изоморфизма.

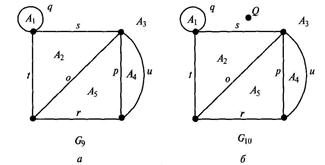
Граф G называется планарным (плоским),если существует изоморфный ему граф G', в изображении которого на плоскости ребра пересекаются только в вершинах. Иными словами, у планарного графа никакие два ребра не имеют общих точек, кроме общих вершин. На рис. 2.1 графы G₁ и G₃ являются планарными, а G₂ — нет. Областьюназовем подмножество плоскости, пересекающееся с планарным графом только по некоторому проcтому циклу графа, являющемуся границей области. Поскольку рассматриваются конечные графы, то плоский граф всегда является ограниченным подмножеством плоскости. Пусть М — планарный граф с внутренними областями. Тогда дополнение М, т. е. М' = К²М также может являться областью. Например, граф О₉ (рис. 2.6, а) выделяет в плоскости следующие области: А с границей д; А% с границей (о, 5, I)', А₃с границей (д, 5, и, г, {); А^с границей (р, и); А₅ с границей (о, р, г). Множество А_ъ на рис. 2.6, б областью не является, так как пересечение Л₃П С₁₀ содержит точку (2, не принадлежащую никакому циклу.

Рис. 2.5. Изоморфные графы	Рис. 2.6. Графы: а — G9 (с областями А1— A5); б — G10 (с областями А1,A2,, А4, A5)

Теорема 2.5 (Эйлера).Связный плоский граф с п вершинами и т ребрами разбивает плоскость на r областей (включая внешнюю), причем

п - т + r= 2.

Задача 17 «О трех колодцах».Проложить дорожки от трех до­мов к каждому из трех колодцев так, чтобы никакие две дорожки не пересекались (рис. 2.7).

Граф называется двудольным,если его вершины разбиты на два непересекающихся подмножества: V= V₁ È V₂, а ребра связывают вершины только из разных классов (не обязательно все пары). Если каждая вершина множества V₁ связана ребром с каждой вершиной множества V₂, то двудольный граф называетсяполным двудольными обозначается К_т,n, где т = | V₁|, n = | V₂|.

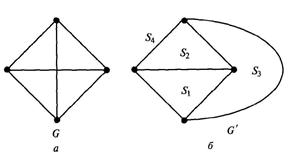
Рис. 2.7. Иллюстрация к задаче «О трех колодцах»	Рис. 2.8. Планарные графы: а — первоначальный; б — изображенный иначе

Примером двудольного полного графа К_3,3, является граф к задаче 17, которую также называют «Три дома — три колодца», показывая этим два непересекающихся множества вершин графа.

На (рис. 2.8, а) граф G является планарным, так как его можно изобразить иначе (G' на рис. 2.8, б). При таком изображении плоскость разбивается на области S₁, S₂, S₃, S₄, которые могут быть раскрашены в разные цвета. Видно, что п = 4, т = 6, r = 4, и справедлива формула Эйлера п-т + r=4-6 + 4 = 2.

Рис. 2.9. Изображение эйлерова графа	Рис. 2.10. Изображение гамильтоновых путей

Эйлеровым путем (циклом)графа G называется путь (цикл), который содержит все ребра графа только один раз. Граф, обладающий эйлероовым циклом, называется эйлеровым.Плоские эйлеровы графы можно изобразить «одним росчерком пера», причем процесс изобжения начинается и заканчивается в одной вершине. Такой граф называют также уникурсальным.

Теорема 2.6.Граф G является эйлеровым тогда и только тогда, когда G — связный граф, имеющий все четные вершины.

На рис. 2.9 изображен пример эйлерова графа. Граф G₉ на рис. 2.6, а не будет эйлеровым, так как не все его вершины являются четными.

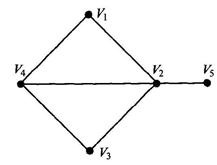
Гамильтоновым путем (циклом) графа G называется путь (цикл), проходящий через каждую его вершину только один раз. Граф, содержащий гамильтонов цикл, называется гамильтоновым.

Например, в графе G путь (V₃, V ₄, V ₁, V ₂, V ₅) является гамильтоновым, а путь (V ₂, V ₃, V ₄, V ₁ V ₂, V ₅) не является гамильтоновым (рис. 2.10).

Задача 18 «О кенигсбергских мостах»(Эйлера). Необходимо обойти все 7 мостов так, чтобы на каждом побывать только один раз и вернуться к началу пути (рис. 2.11, а).

Граф к задаче о мостах изображен на рис. 2.11, б.

Задача Эйлера «О кенигсбергских мостах».Историческим поводом для создания математической науки, получившей впоследствии название «Теория графов», явилось решение в 1736 г. Л.Эйлером задачи о кенигсбергских мостах. В XVIII в. город Кенигсберг располагался на двух берегах реки Преголи, имеющей два острова, соединенных с берегами и между собой семью мостами. Жители города на практике решали задачу: можно ли пройти по всем семи мостам так, чтобы на каждом из них побывать по одному разу и вернуться к началу пути.

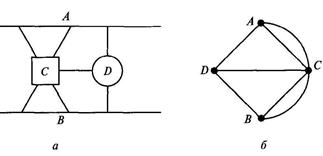
Рис. 2.11. Иллюстрации к задаче «О кенигсбергских мостах»: а — условие; б — граф.

Задача Кэли «О четырех красках».Принята такая формулировка этой задачи: на любой политико-административной карте раскрасить страны четырьмя красками так, чтобы никакие две страны, имеющие общую границу, не были раскрашены одинаковым цветом, причем общей границей не может служить одна точка.

Сформулируем задачу на языке теории графов: в произвольном неориентированном плоском графе G четырьмя красками раскрасить вершины так, чтобы никакие две смежные вершины не были раскрашены одним цветом. Оказывается, условие задачи выполнимо для пяти красок. Даже доказано, что такая раскраска возможна для всех плоских графов с числом вершин, не превосходящим 38. Но проблема четырех красок остается нерешенной с 1878 г., когда английский математик Кэли привел ее формулировку на заседании Английского королевского научного общества.

Задача «О трех домах и трех колодцах».Условие этой задачи нам известно: «Проложить дорожки от трех домов к каждому из трех колодцев так, чтобы никакие две дорожки не пересекались». Эта задача была решена Куратовским в 1930 г.

Деревья. Лес. Бинарные деревья

Я. Таранов Деревомназывают конечный связный граф с выделенной вершиной (корнем),не… Для каждой пары вершин дерева — узлов— существует единственный маршрут, поэтому вершины удобно классифицировать по…

Способы задания графа. Изоморфные графы

В математике значительно сильнее, чем в других дисциплинах, обнаруживается черта организованности, стремление находить скрытый порядок во всем, что нас окружает...

А. Сухотин

Существуют различные способы задания графа: геометрический (рисунки, схемы, диаграммы), простое перечисление вершин и ребер, табличный. Человеку удобно работать с графом-рисунком, так как он может легко установить связь между вершинами в наглядном виде с помощью ребер, изображаемых непрерывными линиями. Такое геометрическое представление плоского графа называется его реализацией.Для машинной обработки удобнее задать граф в алгебраической форме — перечислением (списком) вершин или ребер.

Например, орграф на рис. 2.3 можно задать с помощью пар (V₁, V₂), (V₂, V₃), (V₂, V₃) и (V₁, V₁), что соответствует дугам (r, и, t, s). При переходе от алгебраического способа к геометрическому одному и тому же графу могут соответствовать различные изображения — изоморфные графы,при этом от правильного изображения зависит, например, свойство плоской реализуемости. Для этого нужно правильно задать сам граф.

Основным способом задания графа является перечисление всех его вершин и ребер. Но такое представление, во-первых, несимметрично (с ним трудно работать, особенно ЭВМ), во-вторых, для указания каждого ребра нужно еще раз выписывать соответствующие вершины, что плохо с точки зрения сжатия и хранения информации. Иногда граф задается таблицей,состоящей из п строк (вершины) и т столбцов (ребра). Главным во всех способах задания графа (диаграммой, матрицей, таблицей) является указание соответствия между множествами п вершин V_i и т ребер X _i.

Одним из самых распространенных способов задания графа является матричный способ.Пусть дан граф G(V, X), где V={V₁, V₂, ..., V_п} — вершины, а Х= {Х₁, Х₂, ..., Х_т} — ребра графа.

Назовем матрицей инцидентноститаблицу В, состоящую из п строк (вершины) и т столбцов (ребра), в которой:

для неориентированного графа:

b_ij = 1, если вершина V_i инцидентна ребру X_j;

b_ij = 0, если вершина V_i не инцидентна ребру X_j;

для ориентированного графа:

b_ij = 1, если вершина V_i является началом дуги X_j,

b_ij =0, если вершина V_i не инцидентна дуге X_j,

b_ij = -1, если вершина V_i является концом дуги X_j.

Очевидно, что в каждом столбце матрицы инцидентности должно быть только два ненулевых числа, так как ребро инцидентно двум вершинам. Число ненулевых элементов каждой строки — степень соответствующей вершины. Но в математике удобнее работать с квадратными матрицами, так как для них хорошо разработан соответствующий алгебраический аппарат.

Назовем матрицей смежностиграфа G( V, X) без кратных ребер квадратную матрицу А порядка я, в которой:

a_ij = 1, если (V_i,, V_j) ÎX;

a_ij =0, если (V_i,, V_j} Ï X.

Поскольку для неориентированного графа ребра (V_i,, V_j) и (V_j,, V_i) одновременно принадлежат или не принадлежат графу, так как символизируют одно и то же ребро, то a_ij == a_ji. Матрица смежности неориентированного графа является симметрической и не меняется при транспонировании.

Хотя формально каждая вершина всегда смежна сама с собой, в матрице смежности мы будем ставить a_ij = 0, если у нее нет петли, и a_ij =1, если есть одна петля. Итак, если граф имеет матрицу смежности и не имеет петель, на главной диагонали у него всегда стоят нули.

Например, орграф на рис. 2.3 можно задать такой таблицей инцидентности (табл. 2.1).

Таблица 2.1. Таблица инцидентности орграфа

 

Vi	Xj
s	t	r	u
V1	-1
V2			-1
V3		-1		-1

Его же можно задать матрицей B=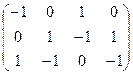

Поскольку ребра изначально не упорядочены, то, например, записывая сначала инцидентность ребра t (1-й столбец), потом ребра s (2-й столбец), получим матрицу с переставленными столбцами 1 и 2. Тогда при решении обратной задачи -восстановлении графа по его матрице инцидентности — можно получить граф лишь с точностью до изоморфизма. Поэтому в графах важно лишь отношение между вершинами (т. е. смежность), а их название и порядок не столь важны.

Граф, изображенный на рис. 2.18, задается таблицей инцидентности (табл. 2.2).

Таблица 2.2. Таблица инцидентности графа

	Xj
Х1	Х2	Х3	Х4	Х5	Х6	Х7	Х8	Х9	Х10
V1
V2
V3
V4
V5
V6

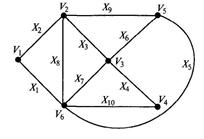
Рис. 2.18. Графическая интерпретация графа G, заданного табл. 2.2

Матрица инцидентности для него имеет вид

Этому же рисунку соответствуют таблица и матрица смежности (табл. 2.3).

Таблица 2.3. Таблица смежности графа G

 

Vi	Vj
V1	V2	V3	V4,	V5	V6
V1
V2
V3
V4
V5
V6

Граф с кратными ребрами (особенно орграф) сложно задать с помощью матрицы смежности. Сделаем это формально. Если граф неориентированный, то справедливо a_ij == a_ji. и равно кратности ребра (V_i, V_j). В частности, если i=j, то a_ij — число петель при V_i. Недостаток подобного подхода заключается в том, что остается неучтенным взаимное расположение кратных ребер. Так, ребра могут переплетаться между собой, что, к сожалению, не отразится на матрице смежности.

Заметим, что для ориентированного графа данное определение графа без кратных ребер является частным случаем графа с кратными ребрами при кратности любого ребра, равной 1 или 0. Очевидно, что для двух вершин V_i и V_j (i¹j) существуют две принципиальные возможности:

если все ребра выходят из одной и входят в другую вершину

или если для каждой вершины существуют как входящие, так и исходящие ребра.

Пусть полная кратность ребра равна n, при этом из вершины V_i в вершину V_j исходят т £ п ребер, а из V_j в V_i исходят п - т ребер. Тогда в клетке a_ij напишем m, а в клетке a_ji напишем п - т. Если есть кратные петли, то все они связаны с одной вершиной V_i. Поэтому в клетке a_ii напишем кратность петли при V_i.

Такому заданию графа присущи те же недостатки, что и неориентированному, и еще неучет взаимного расположения направлений. Однако главным недостатком служит то, что при таком определении матрицы смежности (как графа с кратными ребрами, так и без них) не всегда возможно определить по матрице смежности ориентированный граф или нет.

В матрицах инцидентности такой проблемы нет, так как наличие элемента вида -1 является критерием ориентированности графа. Для матрицы смежности несимметричность может являться достаточным условием ориентированности, но не критерием. Например, графу с матрицей смежности может соответствовать отрезок V₁ V₂ (и две вершины) — неориентированный граф или кольцо с двумя ребрами V = {( V₁, V₂); ( V₂, V₁)} — орграф. Это -существенный недостаток, и возник он как раз при попытке определения матрицы смежности для графа с кратными ребрами Поэтому для задания ориентированного графа с помощью матрицы смежности (если она получается симметричной) надо или указывать это отдельно, например А_ор , или у любого элемента матрицы написать «-».

Задача 19.Пусть граф G задан матрицей смежности А. Построить диаграмму этого графа, если

 

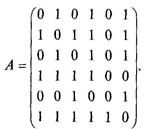Решение. Поскольку матрица А несимметрична (например a₃₅¹a₅₃) и указания на ориентированность нет, А не может яляться матрицей смежности реального графа.

Задача 20.Пусть граф G задан матрицей смежности А. Построить диаграмму этого графа, если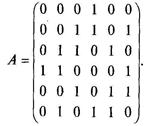

Решение. Диаграмму графа, имеющего шесть вершин, представим на рис. 2.19.

Любой ориентированный граф является бинарным отношением А под V, где V— множество вершин графа, а пары из X— ребра.

Для конечного числа V вершин отношение X можно представить тремя способами:

графически, т.е. диаграммой (рис. 2.19);

с помощью таблиц, в которых представлены 1 и 0;

с помощью матриц (в случае матриц смежности).

Такая форма записи отношений удобна при решении многих логических и производственных задач. Она также используется при машинной обработке для систематизации информации

Рис. 2.19. Граф к задаче

 

Сети. Сетевые модели представления информации

А. Сухотин Граф называется взвешеннымили сетью,если каждому его ребру поставлено в… В строительстве сетевые графы применяются для наглядного изображения некоторого комплекса работ или производственных…

Применение графов и сетей

Латинская формула Сети получили широкое практическое применение потому, что они являются…  

Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Сформулируйте основные понятия и определения графа и его элементов

2. Дайте определения дерева, леса, бинарного дерева.

3. Укажите способы задания графа. Дайте определение изоморфных графов

4. Дайте примеры сетей и сетевых моделей представления информации

5. Приведите примеры применения графов и сетей