Лекция 4. СОБЫТИЕ И ВЕРОЯТНОСТЬ

Цель: Изучить основные понятия теории вероятности

План:

1.Основные понятия. Определение вероятности

2. Свойства вероятности

3. Вопросы для контроля знаний и подведения итога прочитанной лекции

1. Основные понятия. Определение вероятности

1. Понятие о случайном событии. Опыт, эксперимент, наблюдение явления называется испытанием. Испытаниями, например, являются бросание монеты, выстрел из винтовки, бросание игральной кости (кубика с нанесенными на каждую грань числом очков — от одного до шести).

Результат, исход испытания, называется событием. Событиями являются выпадение герба или цифры, попадание в цель или промах, появление того или иного числа очков на брошенной игральной кости.

Для обозначения событий используют прописные (большие) буквы латинского алфавита: А, В, С и т.д.

Определение 1. Два события называют совместимыми, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример 8.1. Испытание — однократное бросание игральной кости. Событие А — появление четырех очков. Событие В — появление четного числа очков. События А и В совместимые.

Определение 2. Два события называют несовместимыми, если появление одного из них исключает появление другого в одном и том же испытании.

Пример 8.2. Испытание — однократное бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события несовместимы, так как появление одного из них исключает появление другого.

Несовместимость более чем двух событий означает их попарную несовместимость.

Пример 8.3. Испытание — однократное бросание игральной кости. Пусть события А₁, А₂, А₃, А₄, А₅, А₆ — соответственно выпадение одного очка, двух, трех и т.д. Эти события являются несовместимыми.

Определение 3. Два события А и В называются противоположными, если в данном испытании они несовместимы и одно из них обязательно происходит.

Событие, противоположное событию А, обозначают через .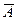

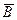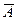Пример 8.4. Испытание — однократное бросание монеты. Событие А — выпадение герба, событие В — выпадение цифры. Эти события противопо­ложны, так как исходами бросания могут быть лишь они, и появление одного из них исключает появление другого, т.е. А = или = В.

Определение 4. Событие называют достоверным, если в данном испытании оно является единственно возможным его исходом, и невозможным, если в данном испытании оно заведомо не может произойти.

Пример 8.5. Испытание — извлечение шара из урны, в которой все шары белые. Событие А — вынут белый шар — достоверное событие; событие В — вынут черный шар — невозможное событие.

Заметим, что достоверное и невозможное события в данном испытании являются противоположными.

Определение 5. Событие А называют случайным, если оно объективно может наступить или не наступить в данном испытании.

Пример 8.6. Событие А₆ — выпадение шести очков при бросании игральной кости — случайное. Оно может наступить, но может и не наступить в данном испытании.

Пример 8.7. Событие А₉₈ — прорастание девяноста восьми зерен пшеницы из ста — случайное. Это событие может наступить, но, может быть, прорастет зерен больше или меньше.

Можно ли как-то измерить возможность появления некоторого случайного события? Другими словами, можно ли охарактеризовать эту возможность некоторым числом?

2. Классическое определение вероятности. Всякое испытание влечет за собой некоторую совокупность исходов — результатов испытания, т.е. событий. Во многих случаях возможно перечислить все события, которые могут быть исходами данного испытания.

Определение 1. Говорят, что совокупность событий образует полную группу событий для данного испытания, если его результатом обязательно становится появление хотя бы одного из них.

Приведем примеры полных групп событий: выпадение герба и выпадение цифры при одном бросании монеты; попадание в цель и промах при одном выстреле; выпадение одного, двух, трех, четырех, пяти и шести очков при одном бросании игральной кости.

Рассмотрим полную группу попарно несовместимых событий U₁, U₂, ..., U_n , связанную с некоторым испытанием. Предположим, что в этом испытании осуществление каждого из событий U_i, (i = 1, 2,..., n) равновозможно, т.е. условия испытания не создают преимущества в появлении какого-либо события перед другими возможными.

Определение 2. События U₁, U₂, ..., U_n, образующие полную группу попарно несовместимых и равновозможных событий, будем называть элементарными событиями.

Пример 8.8. Вернемся к опыту с подбрасыванием игральной кости. Пусть U_i — событие, состоящее в том, что кость выпала гранью с цифрой i. Как уже отмечалось, события U₁, U₂, ..., U₆ образуют полную группу попарно несовместимых событий. Так как кость предполагается однородной и симметричной, то события U₁, U₂, ..., U₆ являются и равновозможными т.е. элементарными.

Определение 3. Событие А называют благоприятствующим событию В, если наступление события А влечет за собой наступление события В.

Пример 8.9. Пусть при бросании игральной кости события U₂, U₄ и U₆ — появление соответственно двух, четырех и шести очков и А — событие, состоящее в появлении четного числа очков; события U₂, U₄ и U₆ благоприятствуют событию А.

Определение 4 (классическое определение вероятности).

Вероятностью Р(А) события А называют отношение 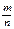числа элементарных событий, благоприятствующих событию А, к числу всех элементарных событий, т. е. .

Пример 8.10. Вычислим вероятность выпадения герба при одном бросании монеты.

Решение. Очевидно, событие А — выпадение герба и событие В — выпадение цифры образуют полную группу несовместимых и равновозможных событий для данного испытания. Значит, здесь n = 2. Событию А благоприятствует лишь одно событие — само А, т.е. здесь т=1. Поэтому Р(А) = Ѕ.

Пример 8.11. Очевидно, что в опыте с игральной костью (пример 8.8)

Р(U_i) = 1/6, i= 1,2, ..., 6.

Пример 8.12. Найдем вероятность того, что при однократном бросании игральной кости выпадет число очков, делящееся на 2 (событие А).

Решение. Число элементарных событий здесь 6, а число благоприятствующих элементарных событий 3 (выпадение 2, 4 и 6), поэтому т =3 и п =6, Р(А ) = 1/2.

Из приведенного классического определения вероятности вытекают следующие ее свойства.

1. Вероятность достоверного события равна единице. Действительно, достоверному событию должны благоприятствовать все п элементарных событий, т.е. т = п и, следовательно,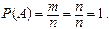

2. Вероятность невозможного события равна нулю. В самом деле, невозможному событию не может благоприятствовать ни одно из элементарных событий, т.е. т = 0, откуда

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных событий. Поэтому в этом случае т < п и, значит, 0 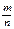_<<1. Следовательно, 0 < Р(А) < 1.

Итак, вероятность любого события удовлетворяет двойному неравенству

0 < Р(А) < 1.

3. Относительная частота. Статистическое определение вероятности. Классическое определение вероятности не является пригодным для изучения произвольных случайных событий. Так, оно неприемлемо, если результаты испытания не равновозможны. Например, при бросании неправильной игральной кости выпадение ее различных граней не равновозможно.

В таких случаях используется, так называемое, статистическое определение вероятности.

Пусть произведено п испытаний, при этом некоторое событие А наступило т раз (т <n).

Определение 1. Число т называют абсолютной частотой (или просто частотой) события А, а отношение называют относительной частотой события А.

Пример 8.13. При транспортировке из 10000 арбузов испортилось 26. Здесь т = 26 — абсолютная частота испорченных арбузов, а 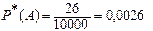- относительная.

Результаты многочисленных опытов и наблюдений помогают заключить: при проведении серий из и испытаний, когда число п сравнительно мало, относительная частота Р^*(А) принимает значения, которые могут довольно сильно отличаться друг от друга. Но с увеличением n — числа испытаний в сериях — относительная частота приближается к некоторому числу Р(А), стабилизируясь возле него и принимая все более устойчивые значения.

Пример 8.14. Было проведено 10 серий бросаний монеты, по 1 000 бросаний в каждой. Относительные частоты выпадения герба оказались равными 0,501; 0,485; 0,509; 0,536; 0,485; 0,488; 0,500; 0,497; 0,494; 0,484 (см. [16]). Эти частоты группируются около числа 0,5.

Определение 2 (статистическое определение вероятности). Вероятностью события А в данном испытании называют число Р(А), около которого группируются значения относительной частоты при больших п.

В условиях только что приведенного примера 8.14 указанная вероятность равна 0,5.

Пример 8.15. По официальным данным шведской статистики относительные частоты рождения девочек по месяцам 1935 г. характеризуются следующими числами (расположены в порядке следования месяцев, начиная с января): 0,486; 0,489; 0,490; 0,471; 0,478; 0,482; 0,462; 0,484; 0,485; 0,491; 0,482; 0,473 (см. [4]). Эти частоты группируются около числа 0,482.

Экспериментавтор	Число бросаний	Число выпаде-ний герба	Относите-льная частота
Бюффон			0,5080
К. Пирсон			0,5016
К. Пирсон			0,5005

Таким образом, относительная частота события приближенно совпадает с его вероятностью, если число испытаний достаточно велико. Имеется огромный опытный материал по проверке последнего утверждения. Укажем еще один такой пример с бросанием монеты (см. таблицу выше)

Здесь относительные частоты незначительно отклоняются от числа 0,5, причем тем меньше, чем больше число испытаний. При 4040 испытаниях отклонение равно 0,008, а при 24000 — 0,0005.

Пример 8.16. Чтобы знать, какова вероятность для данного станка изготовить годную деталь, поступают так: проверяют одну или несколько партий деталей, изготовленных станком, подсчитывают число годных деталей, вычисляют относительную частоту и в соответствии с определением веро­ятность принимают равной этой частоте. Допустим, при проверке партии из 200 деталей 190 оказались годными. Тогда вероятность наудачу выбран­ной детали быть годной равна

Р^*(А)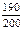_{= =} 0,095.

Вероятность найдена приближенно, так как 0,95 — это относительная частота.

Аналогичным образом поступают, например, при определении процента всхожести семян.

4. Основные формулы комбинаторики. Комбинаторика — раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).

Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них.

Определение 1. Размещениями из п различных элементов по т элементов (т ≤ п) называют комбинации, составленные из данных п элементов по т элементов, которые отличаются либо самими элементами, либо порядком элементов.

Например, из трех элементов а, b, с можно составить по два элемента следующих размещений:

аb, ас, bс, bа, са, сb.

Число различных размещений из п элементов по т элементов определяется с помощью формулы

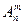=n!/(n-m)!

Пример 8.17. Сколько можно составить сигналов из 6 флажков различного цвета, взятых по 2? Искомое число сигналов =6!/4! = 30.

Определение 2. Перестановками из п различных элементов называют размещения из этих п элементов по п.

Как видно из определений 1 и 2, перестановки можно считать частным случаем размещений при т = п. Следовательно, число всех перестановок из п элементов вычисляется по формуле

 

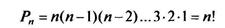
Пример 8.18. Для лечения заболевания применяют три лекарства. Полагают, что последовательность, в которой применяют лекарства, оказывает существенное влияние на результат лечения. Сколько имеется различных порядков назначения этих лекарств?

Решение. Имеется Р₃ =3! = 3-2-1 =6 различных порядков назначения трех лекарств.

Определение 3. Сочетаниями из п различных элементов по т элементов называются комбинации, составленные из данных п элементов по т элементов, которые отличаются хотя бы одним элементом.

Отметим разницу между сочетаниями и размещениями: в первых не учитывается порядок элементов.

Число сочетаний из п элементов по т элементов вычисляется по формуле

 

(8.1)

 

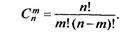или

Отметим особенность формулы (8.1): =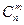

Пример 8.19. В лабораторной клетке содержат трех белых и трех коричневых мышей. Найти число способов выбора двух мышей, если они могут быть любого цвета.

Решение. В данном случае цвет не существен. Поэтому имеется 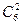=61/(2!(6-2)!)= 61/(2!4!)= 15 способов, которыми двух мышеи можно выбрать из шести.

Приведем, наконец, один из примеров применения формул комбинаторики к нахождению вероятности события.

Пример 8.20. Набирая номер телефона, абонент забыл две последние цифры и, помня лишь, что эти цифры различны, набрал их наудачу. Какова вероятность того, что номер набран правильно?

Решение. Две последние цифры можно набрать способами, а благоприятствовать событию М (цифры набраны правильно) будет только один способ, поэтому

P(М)=1/=1/90.