Непрерывные случайные величины

1. Интегральная функция распределения. Для непрерывной случайной величины в отличие от дискретной нельзя построить таблицу распределения. Поэтому непрерывные случайные величины изучают другим способом, который мы сейчас рассмотрим. Пусть X — непрерывная случайная величина с возможными значениями из некоторого интервала (а; b) и х — действительное число. Под выражением Х<х понимается событие «случайная величина Л' приняла значение, меньшее х». Вероятность этого события Р(Х< х) есть некоторая функция переменной х

Р(х) = Р(Х < х).

Определение. Интегральной функцией распределения (или кратко функцией распределения) непрерывной случайной величины X называется функция F(х), равная вероятности того, что X приняла значение, меньшее х:

F(х) = Р(Х < х). (9.4)

Отметим, что функция распределения совершенно также определяется для дискретных случайных величин.

Укажем свойства, которыми обладает функция F(х).

1. 0 £ F(х) £ 1.

Это свойство следует из того, что F(х) есть вероятность.

2. F(х) — неубывающая функция, т.е. если х₁< х₂, то F(х_}) £F(х₂).

Доказательство. Предположим, что х₁ <х₂. Событие «X примет значение, меньшее х₂» можно представить в виде суммы двух несовместимых событий: «X примет значение, меньшее х₁ и «X примет значение, удовлетворяющее неравенствам х₁£ Х< х₂». Обозначим вероятности последних двух событий соответственно через Р(Х< х₁) и Р(х₁£Х<х₂). По теореме о вероятности суммы двух несовместимых событий

 

Р(Х < х₂) = Р(Х< х₁) +Р(х₁£Х<х₂).

откуда с учетом (9.4)

Р(х₁£Х<х₂)= F(х₂)- F(х₁). (9.5)

Так как вероятность любого события есть число неотрицательное, то Р(х₁£Х<х₂)³0 и, значит, F(х₂)³F(х₁).

Формула (9.5) утверждает свойство 3.

5. Вероятность попадания случайной величины Х в полуинтервал [а; b) равна разности между значениями функции распределения в правом и левом концах интервала (а; b):

Р(а£Х<b) = F(b)-F(а). (9.6)

Пример 9.9. Случайная величина X задана функцией распределения

 

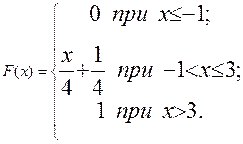
Найдем вероятности того, что в результате испытания X примет значение, принадлежащее полуинтервалу [0; 2).

х

Решение. Так как на полуинтервале [0; 2) F(х) = то

Р(0£Х<2) = F(2)-F(0)=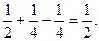

В дальнейшем случайную величину X будем называть непрерывной, если непрерывна ее функция распределения F(х) с непрерывной или кусочно-непрерывной производной.

4. Вероятность того, что непрерывная случайная величина X примет какое-либо заранее заданное значение, равна нулю:

Р(Х = х₁) = 0. (9.7)

Доказательство. Положив в (9.5) х₂ = х₁+ Dх, будем иметь

Р(х₁ £ X < х₁+ Dх) = F(х₁+ Dх) - F(х₁ ). (9.8)

Так как F(х) — непрерывная функция, то, перейдя в (9.8) к пределу при Dх®0, получим искомое равенство (9.7). Из свойства 4 следует свойство 5.

5. Вероятности попадания непрерывной случайной величины в интервал, сегмент и полуинтервал с одними и теми же концами одинаковы

 

Р(a<X <b) = Р(a£ X £ b) = Р(a£ X <b) = Р(a<X £ b) . (9.9)

6. Если возможные значения случайной величины X принад­лежат интервалу (а; b), то 1) F(х) = 0 при х £а; 2) F(х) = 1 при х³b.

Доказательство. 1) Пусть х₁ £а. Тогда событие Х< х₁ невозможно, и, следовательно, вероятность его равна нулю.

2) Пусть х₂ ³ b. Тогда событие X < х₂ достоверно, и, следовательно, вероятность его равна 1.

Следствие. Если возможные значения непрерывной случайной величины расположены на всей числовой оси, то справедливы следующие предельные соотношения:

F(-¥) ==0; F(¥) === 1.

2. Дифференциальная функция распределения. Дифференциальной функцией распределения непрерывной случайной величины ДГ(или ее плотностью вероятности) называется функция f(х) равная производной интегральной функции: f(х) =F’(х)

Так как F(х) — неубывающая функция, то f(х) ³ 0 (см. подразд. 3.7, п. 1).

Теорема 9.3. Вероятность попадания непрерывной случайной величины X в интервал (а; b) равна определенному интегралу от дифференциальной функции распределения величины X, взятому в пределах от а до b:

Р(а<Х<b)=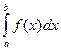 . (9.10)

Доказательство. Так как F(х)является первообразной для f(х), то на основании формулы Ньютона— Лейбница (см. подразд. 4.4, п. 2)

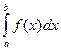=F(b)-F(а). (9.11)

Теперь с учетом соотношений (9.6), (9.9), (9.11) получим искомое равенство.

Из (9.10) следует, что геометрически (см. подразд. 4.3, п. 2) вероятность Р(а<X<b) представляет собой площадь криволинейной трапеции, ограниченной графиком плотности вероятности у =f(х) и отрезками прямых у = 0, х = а и х = b.

Следствие.В частности, если f(х)) — четная функция и концы интервала симметричны относительно начала координат, то

Р(-а<Х<a)= Р(½Х½<a)= 2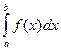 (9.12)

Заменяя в формуле (9.11) а на -¥ и b на х, получаем

F(x)-F(-¥)= .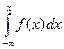

откуда, в силу найденного выше следствия (см. п. 1),

F(x)= 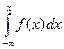. (9.13)

Формула (9.13) дает возможность отыскать интегральную функцию распределения F(x) по ее плотности вероятности.

Отметим, что из формулы (9.13) и из только что отмеченного следствия вытекает, что

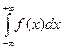=1 (9.14)

Пример 9.10. Задана плотность вероятности случайной величины X

f(x)=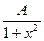(-¥< x < +¥)

Требуется найти коэффициент А, функцию распределения F(х) и вероятность попадания случайной величины Х в интервал (0; 1).

Решение. Коэффициент А найдем, воспользовавшись соотношением (9.14). Так как

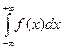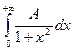==+=A arctg x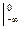+ A arctg x=

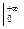= A arctg (+¥)-A arctg (-¥)=Аp,

то Аp = 1, откуда А =1/p.

Применяя формулу (9.13), получаем функцию распределения F(х):

F(х)= 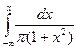=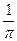A arctg x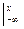=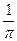[ arctg x- arctg (-¥)]=

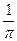==+ arctg x.

Наконец, формулы (9.6) и (9.9) с учетом найденной функции F(х) дают

P(0< x < 1)= F(1)- F(0)= .