Оценки параметров генеральной совокупности по ее выборке

1. Выборка как набор случайных величин.Пусть имеется некоторая генеральная совокупность, каждый объект которой наделен количественным признаком X. При случайном извлечении объекта из генеральной совокупности становится известным значение х признака X этого объекта. Таким образом, мы можем рассматривать извлечение объекта из генеральной совокупности как испытание, X — как случайную величину, а х — как одно из возможных значений X.

Допустим, что из теоретических соображений удалось установить, к какому типу распределений относится признак X. Естественно, возникает задача оценки (приближенного нахождения) параметров, которыми определяется это распределение. Например, если известно, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить, т.е. приближенно найти математическое ожидание и среднее квадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение.

Обычно в распоряжении исследователя имеются лишь данные выборки генеральной совокупности, например значения количественного признака x₁, x₂, …, x_n полученные в результате п наблюдений (здесь и далее наблюдения предполагаются независимыми). Через эти данные и выражают оцениваемый параметр.

Опытные значения признака X можно рассматривать и как значения разных случайных величин Х₁, Х₂,..., Х_n с тем же распределением, что и X, и, следовательно, с теми же числовыми характеристиками, которые имеет X. Значит, М(Х_i) = М(Х) и D(Х_i) = D(Х). Величины Х₁, Х₂,..., Х_n можно считать независимыми в силу независимости наблюдений. Значения x₁, x₂, …, x_n в этом случае называют реализациями случайных величин Х_{, Х_г,..., Х„. Отсюда и из предыдущего следует, что найти оценку неизвестного параметра — значит найти функцию от наблюдаемых случайных величин Х₁, Х₂,..., Х_n, которая и дает приближенное значение оцениваемого параметра.

4. Генеральная и выборочная средние. Методы их расчета.Пусть изучается дискретная генеральная совокупность объема N относительно количественного признака X.

Определение 1. Генеральной средней 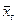(или а) называется среднее арифметическое значений признака генеральной совокупности.

Если все значения x₁, x₂, …, x_N признака генеральной совокупности объема N различны, то

Если же значения признака x₁, x₂, …, x_k имеют соответственно частоты N₁, N₂, …, N_k, причем N₁+N₂+…+ +N_k,=N то

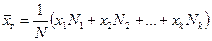
или

(10.1)

Как уже отмечалось (см. п. 1), извлечение объекта из генеральной совокупности есть наблюдение случайной величины X.

Пусть все значения x₁, x₂, …, x_N различны. Так как каждый объект может быть извлечен с одной и той же вероятностью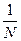, то

т.е.

М(Х) = 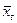. (10.2)

Такой же итог следует, если значения x₁, x₂, …, x_k имеют соответственно частоты N₁, N₂, …, N_k.

В случае непрерывного распределения признака X по определению полагают 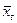= М(Х).

Пусть для изучения генеральной совокупности относительно количественного признака X произведена выборка объема n.

Определение 2. Выборочной средней 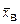называется среднее арифметическое значений признака у выборки из совокупности.

Если все значения x₁, x₂, …, x_n признака выборки объема п различны, то

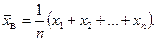(10.3)

 

Если же значения признака x₁, x₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k, причем n₁+ n₂+…+n_k=n, то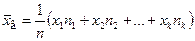

или

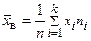(10.4)

Пример 10.4.Выборочным путем были получены следующие данные о массе 20 морских свинок при рождении (г): 30, 30, 25, 32, 30, 25, 33, 32,29, 28, 27, 36, 31, 34, 30, 23, 28, 31, 36, 30. Найдем выборочную среднюю .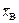

Решение. Согласно формуле (10.4)

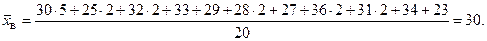
Итак, 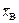= 30 г.

Здесь для облегчения вычислений можно использовать калькулятор. То же следует иметь в виду и в ряде других примеров этой лекции.

Ниже, не уменьшая общности рассуждений, будем считать значения x₁, x₂, …, x_n признака различными.

Разумеется, выборочная средняя для различных выборок того же объема п из той же генеральной совокупности будет получаться, вообще говоря, различной. И это не удивительно — ведь извлечение i-го по счету объекта есть наблюдение случайной величины X_i, а их среднее арифметическое 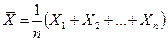есть тоже случайная величина.

Таким образом, всевозможные могущие получиться выборочные средние есть возможные значения случайной величины 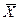, которая называется выборочной средней случайной величиной.

Найдем М(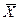), пользуясь тем, что М(Х_i) = М(Х) (см. п. 1).

С учетом свойств математического ожидания (см. предыдущую лекцию) получаем

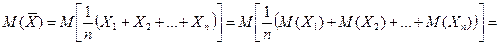
Итак, М(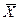) (математическое ожидание выборочной средней) совпадает с а (генеральной средней).

Теперь найдем D(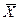). Так как D(Х_i)=D(Х) (п. 1) и X₁, X₂, …, X_n независимы, то согласно свойствам дисперсии (см. предыдущую лекцию) получаем

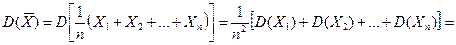
т. е.

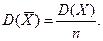(10.5)

Наконец, отметим, что если варианта х_i — большие числа, то для облегчения вычисления выборочной средней применяют следующий прием. Пусть С — константа.

Так как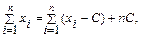

то формула (10.3) преобразуется к виду

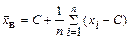(10.6)

Константу С (так называемый, ложный нуль) берут такой, чтобы, во-первых, разности х_i-С были небольшими и, во-вторых, число С было по возможности «круглым».

Пример 10.5. Имеется выборка: х₁=71,88; х₂=71,93; х₃=72,05; х₄=72,07; х₅=71,90; х₆=72,02; х₇=71,93; х₈=71,77; х₉=72,11; х₁₀=71,96.

Найдем среднюю выборочную.

Решение. Берем С=72,00 и вычисляем разности a_i=х _i-С:

a₁=-0,12; a₂=-0,07; a₃=0,05; a₄=0,07; a₅=-0,10; a₆=0,02; a₇=-0,07; a₈=-0,23; a₉=0,11; a₁₀ =-0,04.

Их сумма

a₁+a₂ +.... +a₁₀ = -0,38,

их среднее арифметическое

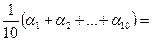= -0,038 » -0,04.

Тогда, выборочная средняя

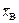»72,00-0,04 = 71,96.

5. Генеральная и выборочная дисперсии. Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят следующую характеристику — генеральную дисперсию.

Определение 1. Генеральной дисперсией D_г. называют среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней .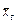

Если все значения x₁, x₂, …, x_N признака генеральной совокупности объема N различны, то

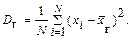
Если же значения признака x₁, x₂, …, x_k имеют соответственно частоты N₁, N₂, …, N_k, причем N₁+N₂,+…+ +N_k=N, то

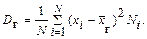(10.7)

Пример 10.6. Генеральная совокупность задана таблицей распределения:

хi
Ni

Найдем генеральную дисперсию.

Решение. Согласно формулам (10.1) и (10.7)

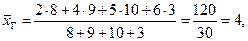
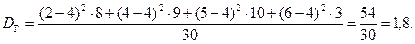
Генеральным средним квадратическим отклонением (стандартом) называется s_г=

Пусть все значения x₁, x₂, …, x_N различны.

Найдем дисперсию признака X, рассматриваемого как случайная величина:

D(Х)=М[((Х)-М(Х))²].

Так как М(Х)=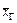и Р{Х= х_i}=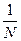(см. п. 2), то

т. е. D(Х)=D_Г.

Таким образом, дисперсия D(Х) равна D_Г.

Такой же итог следует, если значения x₁, x₂, …, x_k имеют соответственно частоты N₁, N₂, …, N_k.

В случае непрерывного распределения признака X по определению полагают

D_Г =D(Х). (10.8)

С учетом формулы (10.8) формула (10.5) (п. 2) перепишется в виде

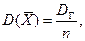
откуда 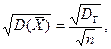или 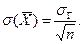. Величину 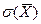называют средней квадратической ошибкой.

Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 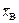, вводят нижеследующую характеристику.

Определение 2. Выборочной дисперсиейD_Вназывается среднее арифметическое квадратов отклонений наблюдаемых значений признака Х от выборочной средней .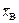

Если все значения x₁, x₂, …, x_n признака выборки объема n различны, то

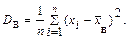(10.9)

Если же значения признака x₁, x₂, …, x_k имеют соответственно частоты n₁, n₂, …, n_k, причем n₁+n₂+…+n_k=n, то

(10.10)

Пример 10.7.Выборочная совокупность задана таблицей распределения:

хi
Ni

Найдем выборочную дисперсию.

Решение. Согласно формулам (10.4) и (10.10)

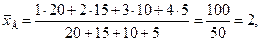
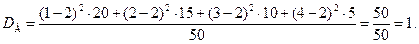
Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии: s_в=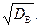

В условиях примера 10.5 получаем, что s_в=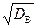==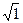1. Ниже, не уменьшая общности рассуждений, будем считать значения x₁, x₂, …, x_n признака различными.

Выборочную дисперсию, рассматриваемую нами как случайную величину, будем обозначать: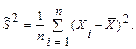

Справедлива (см. например, [2]) следующая теорема.

Теорема 10. 1. Математическое ожидание выборочной дисперсии равно — , т. е. .

В заключение настоящего пункта отметим, что если варианты х_i — большие числа, то для облегчения вычисления выборочной дисперсии D_в формулу (10.9) преобразуют к следующему виду:

где С — ложный нуль.

7.Оценки параметров распределения.Уже говорилось (см. п. 1) о том, что одной из задач статистики является оценка параметров распределения случайной величины X по данным выборки. При этом в теоретических рассуждениях считают, что генеральная совокупность бесконечна. Это делается для того, чтобы можно было переходить к пределу при n®¥, где n — объем выборки. Для оценки параметров распределения X из данных выборки составляют выражения, которые должны служить оценками неизвестных параметров. Например, 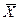(см. п. 2) является оценкой генеральной средней, 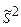(см. п. 3) — оценкой генеральной дисперсии 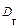. Обозначим через Q оцениваемый параметр, через — оценку этого параметра (является выражением, составленным из X₁, X₂, …, X_n (см. п. 1)). Для того чтобы оценка давала хорошее приближение, она должна удовлетворять определенным требованиям. Укажем эти требования.

Несмещенной называют оценку , математическое ожидание которой равно оцениваемому параметру 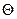, т.е. M()=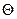, в противном случае оценка называется смещенной.

Пример 10.8.Оценка 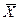является несмещенной оценкой генеральной средней а, так как М(Х}=а (см. п. 2).

Пример 10.9. Оценка 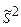является смещенной оценкой генеральной дисперсии 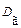, так как согласно установленной выше теореме (см. п. 3) .

Пример 10.10. Наряду с выборочной дисперсией 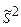рассматривают еще так называемую исправленную дисперсию 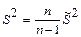, которая является также оценкой генеральной дисперсии. Для S² с учетом установленной выше теоремы (см. п. 3) имеем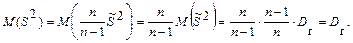

Таким образом, оценка S² в отличие от оценки 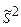является несмещенной оценкой генеральной дисперсии. Явное выражение для S² имеет вид

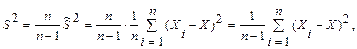
т.е.

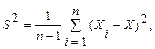(10.11)

Естественно в качестве приближенного неизвестного параметра брать несмещенные оценки, для того чтобы не делать систематической ошибки в сторону завышения или занижения.

Состоятельной называют такую оценку параметра Q, что для любого наперед заданного числа e> 0 вероятность Р{|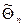-Q|<e} при n®¥ стремится к единице (в таком случае говорят, что 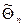сходится к Q по вероятности) . Это означает, что при достаточно больших п можно с вероятностью, близкой к 1, т.е. почти наверное, утверждать, что оценка 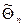отличается от оцениваемого параметра Q меньше чем на e.

Очевидно, такому требованию должна удовлетворять всякая оценка, пригодная для практического использования.

Заметим, что несмещенная оценка 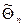будет состоятельной, если при n®¥ ее дисперсия стремится к нулю: D(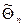) ®0.

Пример 10.11. Как было установлено ранее (см. п. 3), 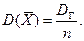Отсюда следует, что несмещенная оценка 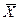является и состоятельной, так как

Можно показать, что несмещенная оценка S² является также состоятельной. Поэтому в качестве оценки генеральной дисперсии принимают исправленную дисперсию. Заметим, что оценки S² и 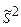отличаются множителем 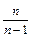, который стремится к 1 при n®¥. На практике S² и 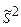не различают при n>30.

Для оценки генерального среднего квадратического отклонения используют исправленное среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии:

(10.12)

Левые части формул (10.11), (10.12), в которых случайные величины X₁, X₂, …, X_n заменены их реализацией x₁, x₂, …, x_n и 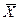— выборочной средней 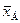, будем обозначать соответственно через s² и s.

Отметим, что если варианты х_i — большие числа, то для облегчения вычисления s² формулу для s² аналогично формуле (10.9) преобразуют к виду

 

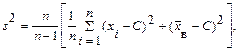(10.13)

где С — ложный нуль.

Оценки, обладающие свойствами несмещенности и состоятельности, при ограниченном числе опытов могут отличаться дисперсиями.

Ясно, что чем меньше дисперсия оценки, тем меньше вероятность грубой ошибки при определении приближенного значения параметра. Поэтому необходимо, чтобы дисперсия оценки была минимальной. Оценку, обладающую таким свойством, называют эффективной.

Из отмеченных требований, предъявляемых к оценке, наиболее важными являются требования несмещенности и состоятельности.

Пример 10.12. С плодового дерева случайным образом отобрано 10 плодов. Их массы x₁, x₂, …, x₁₀ (в граммах) записаны в первой колонке приведенной ниже таблицы. Обработаем статистические данные выборки. Для вычисления 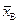и s по формулам (10.6) и (10.13) введем ложный нуль С =250 и все необходимые при этом вычисления сведем в таблицу.

i	хi	хi-С	(хi-С)2
		-25
		-30
		-5
		-39
		-16
		-20
		-19
Сумма		-72

Следовательно ,

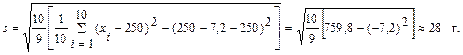
Отсюда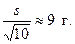

Итак, оценка генеральной средней массы плода равна 243 г со средней квадратической ошибкой 9 г.

Оценка генерального среднего квадратического отклонения массы пло­да равна 28 г.