рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Преобразование тригонометрических выражений.
Реферат Курсовая Конспект
Преобразование тригонометрических выражений.
Преобразование тригонометрических выражений. - раздел Математика, Арифметические вычисления. Проценты 1º. На Плоскости Xoy Рассмотрим Окружность С Цент...
1º. На плоскости xOy рассмотрим окружность с центром в начале координат и радиусом, равным 1. На единичной окружности отметим точку A(1;0). Радиус OA называют начальным радиусом. При повороте начального радиуса на угол α около центра О точка А(1;0) перейдет в некоторую точку М(x;y). Заметим, что поворот можно осуществить по часовой стрелки (угол поворота положителен) или против часовой стрелки (угол поворота отрицателен).
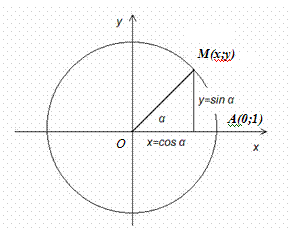 Косинусом угла α называется абсцисса точки М:
Косинусом угла α называется абсцисса точки М: 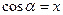 .
.
Синусом угла α называется ордината точки М: 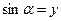 .
.
Тангенсом угла α называется отношение ординаты точки М к ее абсциссе:  .
.
Котангенсом угла α называется отношение абсциссы точки М к ее ординате: 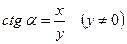 .
.
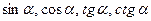 являются тригонометрическими функциями аргумента α.
являются тригонометрическими функциями аргумента α.
2º. Единицами измерения величины угла являются градус и радиан.
Если начальный радиус окружности совершит один полный оборот, то получится угол, равный 360˚ или 2π радиан.
Связь между градусной и радианной мерами измерения угла: 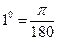 рад.
рад.
Из этой формулы следует:
а) 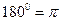 ; б)
; б) 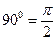 ; в)
; в) 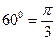 ; г)
; г) 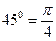 ; д)
; д) 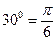 и т.д.
и т.д.
3º. Свойства тригонометрических функций:
Функции 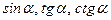 - нечетные функции:
- нечетные функции:
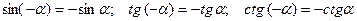 .
.
Функция  - четная:
- четная: 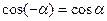 .
.
Функции  - периодические с наименьшим периодом 2π:
- периодические с наименьшим периодом 2π:
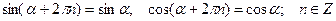 .
.
Функции 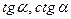 - периодические с наименьшим периодом π:
- периодические с наименьшим периодом π:
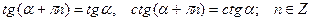 .
.
4º. Основное тригонометрическое тождество.
Согласно теореме Пифагора (“в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы”) координаты любой точки М(x;y) единичной окружности удовлетворяют уравнению: 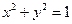 . Отсюда:
. Отсюда:
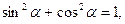 где
где 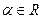 (10.1)
(10.1)
Из этой формулы следует:
а)  ; б)
; б) 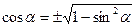 .
.
5º. Основные соотношения между тригонометрическими функциями:
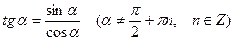 , (10.2)
, (10.2)
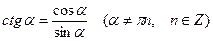 , (10.3)
, (10.3)
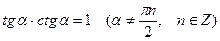 , (10.4)
, (10.4)
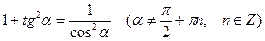 , (10.5)
, (10.5)
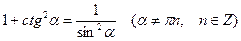 . (10.6)
. (10.6)
6º. Формулы сложения аргументов:
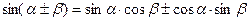 , (10.7)
, (10.7)
 , (10.8)
, (10.8)
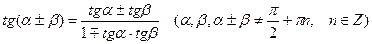 . (10.9)
. (10.9)
7º. Формулы двойного аргумента:
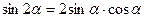 , (10.10)
, (10.10)
 , (10.11)
, (10.11)
 . (10.12)
. (10.12)
8º. Формулы понижения степени синуса и косинуса:
 . (10.13)(10.14)
. (10.13)(10.14)
9º. Преобразование суммы и разности одноименных тригонометрических функций в произведение:
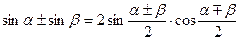 , (10.15)
, (10.15)
 , (10.16)
, (10.16)
 , (10.17)
, (10.17)
 . (10.18)
. (10.18)
10º. Преобразование произведения тригонометрических функций в сумму:
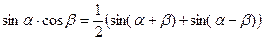 , (10.19)
, (10.19)
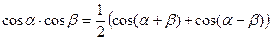 , (10.20)
, (10.20)
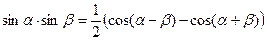 . (10.21)
. (10.21)
11º. Выражение тригонометрических функций через тангенс половинного аргумента.
При доказательстве тождеств, решении тригонометрических уравнений и т.п. часто возникает необходимость выразить все 4 тригонометрические функции через какую-нибудь одну функцию f(x). Для этого пользуются следующими формулами:
а) 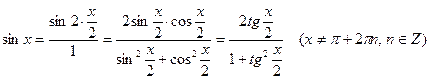 , (10.22)
, (10.22)
б) 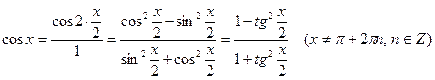 , (10.23)
, (10.23)
в) 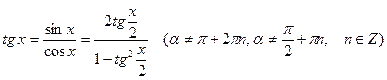 . (10.24)
. (10.24)
12º. Формулы приведения. Это соотношения, при помощи которых значения тригонометрических функций аргументов  выражают через тригонометрические функции угла α. Все формулы приведения можно свести в следующую таблицу:
выражают через тригонометрические функции угла α. Все формулы приведения можно свести в следующую таблицу:
| Аргумент t Функция | 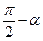
| 
| 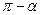
| 
| 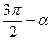
| 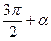
| 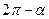
| 
|
| sin t | cos α | cos α | sin α | - sin α | -cos α | -cos α | -sin α | sin α |
| cos t | sin α | -sin α | -cos α | -cos α | -sin α | sin α | cos α | cos α |
| tg t | ctg α | -ctg α | -tg α | tg α | ctg α | -ctg α | -tg α | tg α |
| ctg t | tg α | -tg α | -ctg α | ctg α | tg α | -tg α | -ctg α | ctg α |
Пример 34. Найдите 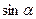 , если
, если 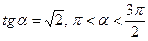 .
.
Решение: 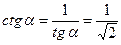 . По формуле (10.6)
. По формуле (10.6) 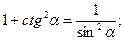
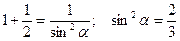 . Так как α находится в 3-ей четверти, то
. Так как α находится в 3-ей четверти, то  и, следовательно,
и, следовательно, 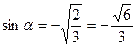 . Ответ:
. Ответ: 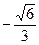 .
.
Пример 35. Вычислить значение выражения 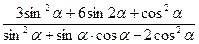 , если
, если 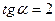 .
.
Решение: Используем формулу (10.10), а затем числитель и знаменатель дроби разделим на 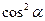 . Тогда:
. Тогда:
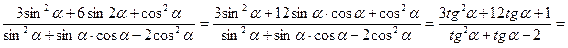
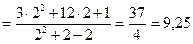
Ответ: 9,25.
Пример 36. Доказать тождество: 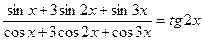 .
.
Решение: Используя формулы (10.15), (10.16), получим:

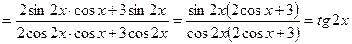 .
.
Пример 37. Вычислить 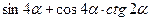 , если
, если  .
.
Решение: Выразив  и
и 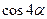 через
через 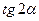 по формулам (10.22), (10.23), получим:
по формулам (10.22), (10.23), получим:
 .
.
Ответ: ¼.
Пример 38. Упростить выражение: 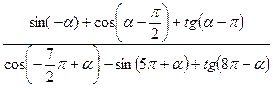 .
.
Решение: Воспользуемся свойствами четности и нечетности тригонометрических функций, а также выделим период в аргументе функций и исключим его, опираясь на свойство периодичности функций:
 ,
,
 ,
,
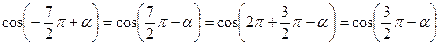 ,
,
 ,
,
 .
.
Получаем: 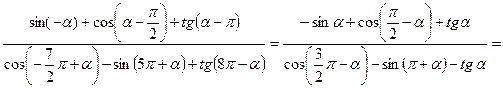
Далее используем формулы приведения:
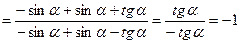 .
.
Ответ: -1.
Пример 39. Найти 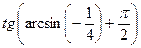 .
.
Решение: Воспользуемся формулой приведения 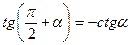 и определением котангенса:
и определением котангенса:
 .
.
Поскольку угол 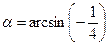 находится в 4-ой четверти
находится в 4-ой четверти  , то
, то 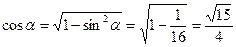 . Получаем:
. Получаем:
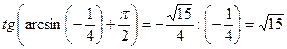 .
.
– Конец работы –
Эта тема принадлежит разделу:
Арифметические вычисления. Проценты
Арифметические вычисления Проценты... Обыкновенные дроби Действия... Тема...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Преобразование тригонометрических выражений.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов