рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- И одностороннего предела).
Реферат Курсовая Конспект
И одностороннего предела).
И одностороннего предела). - раздел Математика, БИЛЕТ 1. Точные грани числовых множеств. Теорема существования Следующие Утверждения Эквивалентны: 1) Существует ...
Следующие утверждения эквивалентны:
1) существует 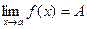
2) существует 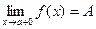 и
и  .
.
1)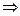 2). Пусть
2). Пусть 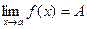 , то есть
, то есть 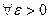
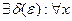
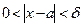
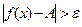 .
.
Обозначим  ,
, 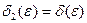 если
если
 , то
, то 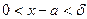 либо
либо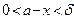 .
.
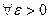

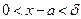
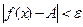
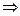
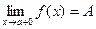 .
.
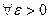

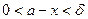

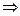
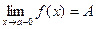 .
.
2)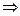 1). Возьмем
1). Возьмем 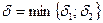 , тогда
, тогда
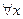

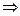
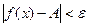
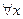

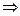
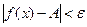
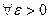
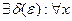

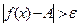
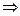
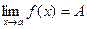 .
.
БИЛЕТ 18. Первый замечательный предел.


Для доказательства возьмем вектор 
окружности радиуса 1 с центральным углом,
равным  (радиан),
(радиан),  и проведем
и проведем
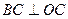 . Тогда пл.
. Тогда пл. 
 < пл. сект.
< пл. сект.
 < пл.
< пл. 
 или
или 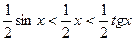 .
.
Разделив все части этого неравенства на
 > 0, получим
> 0, получим
 или
или 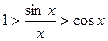 . Это
. Это
неравенство, доказанное для любых  из
из
интервала (0; ), верно для любого
), верно для любого 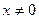 из
из
интервала (- ;
; ) в силу четности функций,
) в силу четности функций,
входящих в это неравенство.
Докажем, что 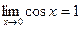
( ) при
) при 
А раз 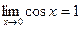 и
и 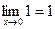 , то
, то  .
.
Кроме того: 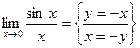 =
=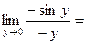 1
1
БИЛЕТ 19. Второй замечательный предел.
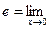
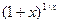 .
.
На первый взгляд кажется, что 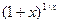 при
при
 имеет пределом единицу (так как 1+
имеет пределом единицу (так как 1+
при  имеет пределом единицу, а единица
имеет пределом единицу, а единица
в любой степени есть единица). Но в степень
 возводится 1+
возводится 1+ , а не единица. И вот из-за
, а не единица. И вот из-за
этой бесконечно малой добавки  предел не равен
предел не равен
единице. Чтобы приблизительно представить себе
поведение функции 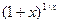 при малых
при малых 
приведем таблицу значений этой функции:

| 1/2 | 1/3 | 1/4 | 0.01 | 0.001 |
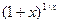
| 2.25 | 2.37… | 2.44… | 2.7047… | 2.7169… |
Из этой таблицы видно, что с уменьшением  функция
функция
увеличивается. Оказывается, что это имеет место для
всех  >0, а из этого следует, что функция имеет предел.
>0, а из этого следует, что функция имеет предел.
Доказательство:
Рассмотрим этот предел, как предел функции
натурального аргумента на бесконечность. Тогда:
По определению Гейне:
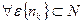
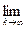
 =
=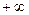

 =
=
Вычислим 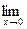
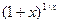 . Рассмотрим
. Рассмотрим
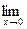
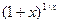 =
=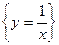 =
=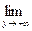
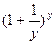 .
.
По определению Гейне рассмотрим 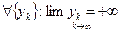 .
.
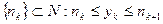
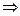




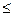
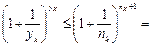
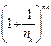 *
*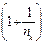
 |



То есть 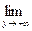
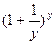 =
= =
= =
=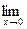
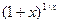 .
.

 Также
Также 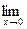
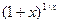 =
= =
=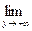
 =
=
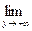
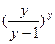 =
=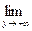

 1
1
БИЛЕТ 20. Сравнение бесконечно малых функций. Примеры.
Определение: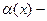 бесконечно малая функция при
бесконечно малая функция при 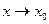 , если
, если 
 .
.
Определение:Пусть 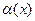 и
и - бесконечно малые функции при
- бесконечно малые функции при 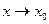 . Тогда:
. Тогда:
1) 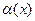 и
и эквивалентны при
эквивалентны при 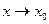 (
(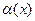 ~
~ ,
,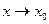 ), если
), если 
 .
.
2)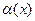 ,
, - бесконечно малые одного порядка малости при
- бесконечно малые одного порядка малости при 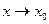 , если
, если 
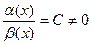 . 3)
. 3)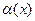 - бесконечно малая более высокого порядка малость, чем
- бесконечно малая более высокого порядка малость, чем  .
.
(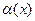 =
=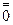 (
( ),
),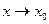 ), если
), если 
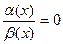 .
.
4).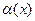 имеет
имеет 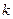 -й порядок малости относительно
-й порядок малости относительно  при
при 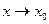 , если
, если 
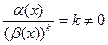 .
.
5). 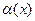 называется ограниченной относительно бесконечно малой функции
называется ограниченной относительно бесконечно малой функции  при
при 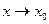 , если
, если 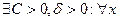
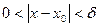
 .
.
Примеры:
1). при
при  .
.
2).  (
( ,
,  -бесконечные малости одного порядка).
-бесконечные малости одного порядка).
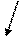
 3).
3). (
(
 )
)
1 0
4). 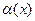 …
…
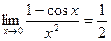 (
( )- 2-й порядок малости относительно
)- 2-й порядок малости относительно  при
при  .
.
5). 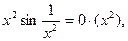

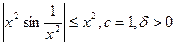 - произвольная.
- произвольная.
БИЛЕТ 21. Эквивалентные бесконечно малые функции. Критерий эквивалентности.
Определение: функция 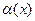 называется бесконечно малой при
называется бесконечно малой при 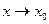 , если
, если 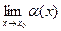 =0.
=0.
Теорема (критерий эквивалентности):
Пусть 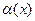 ,
, -бесконечно малые функции при
-бесконечно малые функции при 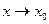 .
.
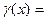
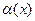 -
- . Тогда
. Тогда 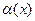 ~
~ при
при 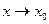
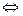
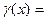
 .
.
Доказательства:
(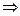 ). Пусть
). Пусть 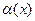 ~
~ ,
, 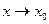 , то есть
, то есть 
 .
.

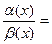
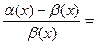

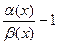 =0,
=0,
то есть 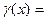
 .
.
(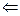 ).
).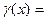
 .,
.,
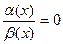 .
.

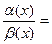


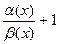 =1.
=1.
БИЛЕТ 22.Эквивалентные бесконечно малые функции. Теорема о замене на эквивалентные.
Определение: функция 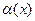 называется бесконечно малой при
называется бесконечно малой при 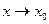 , если
, если 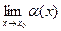 =0.
=0.
Теорема (о замене на эквивалентные):
Пусть функция 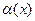 ~
~ ,
,  ~
~ при
при 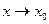 и существует
и существует 
 , тогда существует и
, тогда существует и 
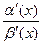 =
=
 . То есть выражение или функцию можно заменять на эквивалентное.
. То есть выражение или функцию можно заменять на эквивалентное.

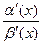 =
=
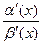 *
*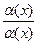 *
* =
=
 .
.
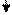 |  |
1 1
БИЛЕТ 23. Определения непрерывности функции в точке. Простейшие свойства непрерывных функций.
Определение 1: Функция  непрерывна в точке
непрерывна в точке  , если
, если  .
.
Определение 2: Функция  непрерывна в точке
непрерывна в точке  , если
, если 
 ,
,  .
.
Определение 3: Функция  непрерывна в точке
непрерывна в точке  , если
, если 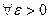
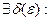
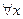

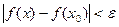 .
.
Свойства непрерывных функций:
Теорема 1 (локальная огр.):Пусть функция  непрерывна в точке
непрерывна в точке  , тогда
, тогда 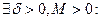
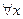
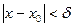
 .
.
Теорема 2 (отделимость от 0):Пусть функция  непрерывна в точке
непрерывна в точке  и
и 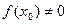 , тогда
, тогда
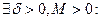
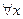
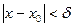
 .
. 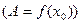 .
.
Теорема 3 (арифметика непрерывных функций):Пусть  ,
, 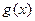 непрерывны в точке
непрерывны в точке  , тогда:
, тогда:
1). 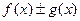 непрерывна в точке
непрерывна в точке  .
.
2).  непрерывно в точке
непрерывно в точке  .
.
3). Если  , то
, то  непрерывно в точке
непрерывно в точке  .
.
БИЛЕТ 24. Непрерывность сложной функции.
Теорема: если функция  непрерывна в точке
непрерывна в точке  , а функция
, а функция 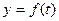 непрерывна в точке
непрерывна в точке 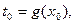 то сложная функция
то сложная функция  непрерывна в точке
непрерывна в точке  .
.
Доказательство:
Возьмем число 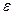 >0. Так как функция
>0. Так как функция  непрерывна в точке
непрерывна в точке 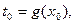 то можно подобрать такое число
то можно подобрать такое число 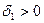 , что
, что
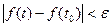 для любого
для любого 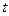 , такого, что
, такого, что  . (1)
. (1)
А так как функция  непрерывна в точке
непрерывна в точке  , то для положительного числа
, то для положительного числа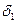 можно подобрать такое число
можно подобрать такое число 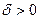 , что
, что
 для любого
для любого  , такого, что
, такого, что 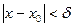 . (2)
. (2)
Возьмем любое число  такое, что
такое, что 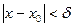 . Тогда в силу (2)число
. Тогда в силу (2)число  удовлетворяет неравенству
удовлетворяет неравенству  , и поэтому в силу (1)
, и поэтому в силу (1) . Так как все эти вычисления проведены для любого
. Так как все эти вычисления проведены для любого 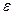 >0, то непрерывность функции
>0, то непрерывность функции  в точке
в точке  доказана.
доказана.
БИЛЕТ 25. Классификация разрывов. Примеры.
Определение:  -точка разрыва функции
-точка разрыва функции  , если в точке
, если в точке функция
функция не является непрерывной.
не является непрерывной.
Определение: точка -точка устранимого разрыва функции
-точка устранимого разрыва функции  , если существует
, если существует 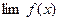 , но
, но  неопределена в точке
неопределена в точке  , либо
, либо  .
.
Замечание: Если в точке устранимого разрыва доопределить (переопределить) функцию:
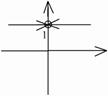
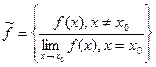 - непрерывна в точке
- непрерывна в точке  .
.
Пример: .
.
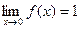 ,
,  - точка устранимого разрыва
- точка устранимого разрыва  .
.
Если  не существует, то
не существует, то  -точка неустранимого
-точка неустранимого
разрыва  .
.
Определение: Пусть точка -точка неустранимого разрыва функции
-точка неустранимого разрыва функции  , тогда:
, тогда:
1) если существует  , то
, то  .
.
2) если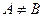 , то
, то  -точка разрыва функции
-точка разрыва функции  1-го рода.
1-го рода.
3) если , то
, то  -точка разрыва функции
-точка разрыва функции  2-го рода.
2-го рода.
 Примеры:
Примеры:
1). 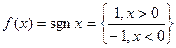 .
.
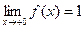 ,
, 
 - точка разрыва
- точка разрыва  1-го рода.
1-го рода.
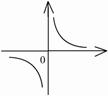 2).
2). 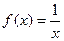 .
.
 ,
, 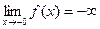
 - точка разрыва
- точка разрыва  2-го рода.
2-го рода.
 3).
3). 
 ,
, 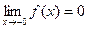
 - точка разрыва
- точка разрыва  2-го рода.
2-го рода.
 4).
4).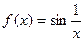
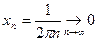

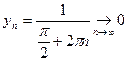

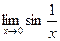 не существует
не существует 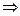 точка
точка  - точка разрыва
- точка разрыва  2-го рода.
2-го рода.
 ,
, 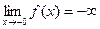 . Точка
. Точка  - точка разрыва
- точка разрыва  2-го рода.
2-го рода.
БИЛЕТ 26. Теорема о нуле непрерывной функции. Теорема Коши о промежуточном значении.
Определение: непрерывна на
непрерывна на 
 , если
, если  непрерывна в точке
непрерывна в точке  ,
,
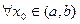
 непрерывна на
непрерывна на 
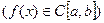 , если
, если  непрерывна в точке
непрерывна в точке  ,
, 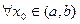 и
и
Существует  ,
, 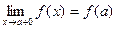 .
.
Теорема:Пусть  определена на
определена на  и
и 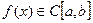 , причем
, причем 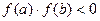 . Тогда
. Тогда
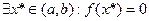 .
.

Пусть  ,
, 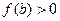 . Используем метод деления отрезка пополам.
. Используем метод деления отрезка пополам.
Обозначим:  ,
, 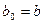 .
.
Определим 
1)  =0
=0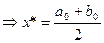 .
.
2)  < 0
< 0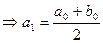 ,
, 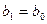 .
.
3)  > 0
> 0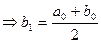 ,
,  и так далее.
и так далее.
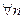
 .
.


 .
.
По лемме о вложенных отрезках: 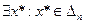
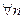 , то есть
, то есть 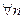
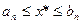 .
.
 непрерывна в точке
непрерывна в точке 
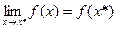 .
.



 .
.
0 (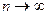 )
)

 .
.



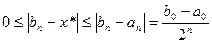 .
. 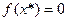
0 (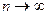 )
)

Следствие (т. о промежуточном значении непрерывной функции):
Пусть 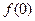 определена на
определена на  и
и 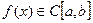 ,
,  ,
,  ,
, 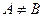
Тогда 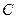 :
: 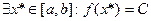 .
.
Пусть для ограничения 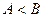 .
.
Рассмотрим произвольн. 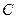 :
: 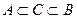
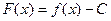 непрерывна на
непрерывна на  .
.

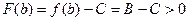
Из этих двух утверждений следует:
 , то есть
, то есть  .
.
БИЛЕТ 27. Первая теорема Вейерштрасса.
Пусть 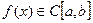 . Тогда
. Тогда  ограничена на
ограничена на .
.
Доказательство:
Докажем, что 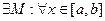
 .
.
Предположим противное, то есть 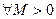

 . Возьмем
. Возьмем  =1,2,3…
=1,2,3…
Получим 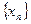 :
:
1) 
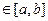
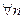
2) 
Из этих определений получаем 
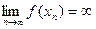 .
.

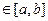 =>
=> 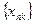 -подпоследовательность последовательности
-подпоследовательность последовательности 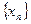 :
:
 .
.
 -непрерывна в точке
-непрерывна в точке  =>
=> 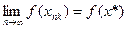 .
.
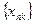 -подпоследовательность последовательности
-подпоследовательность последовательности 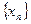 :
: 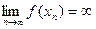 =>
=>  . Противоречие.
. Противоречие.
Замечание:Замкнутость  по существу.
по существу.  ,
, 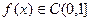 , но
, но 
Не является ограниченной на 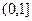 .
.
БИЛЕТ 28. Вторая теорема Вейерштрасса.
Пусть 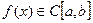 . Тогда
. Тогда 
Замечание: Непрерывная на отрезке  функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу.
функция на этом отрезке достигает своего наибольшего и наименьшего значения, причем в условиях теоремы отрезок по существу.
Доказательство:
По условию теоремы 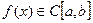 =>
=>  ограничена на
ограничена на  =>
=>  Докажем, что
Докажем, что 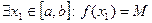 . Предположим противное, то есть
. Предположим противное, то есть 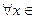

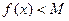 . Рассмотрим вспомогательную функцию
. Рассмотрим вспомогательную функцию 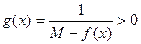 на
на  . По 1 теореме Вейерштрасса
. По 1 теореме Вейерштрасса  ограничена на
ограничена на  , то есть
, то есть 
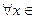
 .
.
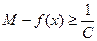
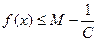
 (<
(< )- верхняя граница.
)- верхняя граница.  , то есть
, то есть 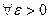
 .
.
Противоречие.
Следствие: если 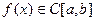 , то
, то  .
.
КОММЕНТАРИЙ:
Опечаток вроде бы не замечено. Но если встретится запись предела при 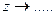 , то следует понимать это как
, то следует понимать это как  (не так-то просто (даже в здравом уме) попасть по клавише «X», вместо «Z»).
(не так-то просто (даже в здравом уме) попасть по клавише «X», вместо «Z»).
– Конец работы –
Эта тема принадлежит разделу:
БИЛЕТ 1. Точные грани числовых множеств. Теорема существования
Точной верхней гранью числового множества называется число такое что... S верхняя граница Для любого положительного числа в множестве M можно найти число такое что...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: И одностороннего предела).
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов