Теорема 1 (свойства счетных множеств).

-Всякое бесконечное множество содержит счетное подмножество.

-Сумма любого конечного или счетного множества счетных множеств есть счетное множества.

-Всякое подмножество счетного множества конечно или счетно.

 

4. Несчетные множества.

Будем называть множество М несчетным, если оно бесконечно и если оно не эквивалентно множеству натуральных чисел (не эквивалентно любому счетному множеству).

Это определение вводит понятие несчетного множества, не являющееся прямым отрицанием понятия счетного множества. В случае прямого отрицания в класс несчетных множеств попадают также и все конечные множества, так как никакое из них не эквивалентно множеству натуральных чисел. Введенные понятия удобнее, так как обычно рассматриваются только бесконечные несчетные множества.

Теорема. Множество всех вещественных чисел отрезка является несчетным.

Доказательство. Допустим противное, т.е. допустим, что множество вещественных чисел указанного отрезка счетно. Тогда все числа этого отрезка можно занумеровать в бесконечную последовательность при помощи натурального ряда чисел: x₁, x₂,_… , x_n,….

Разобьем отрезок на три равные части и обозначим через ту из этих частей, которая не содержит число x₁. Далее отрезок также разобьем на три равные части и обозначим через ту из этих частей, которая не содержит число x₂ и так далее. Продолжая этот процесс, получим бесконечную последовательность отрезков , ,…, которая обладает тремя свойствами:

-каждый последующий отрезок последовательности вложен в непосредственно предыдущий и, значит, во все предыдущие;

-для всякого n N число x_n ;

-при возрастающем n длина отрезка стремится к нулю.

Применим к этой последовательности отрезков теорему из анализа о вложенных отрезках. По этой теореме существует одно и только одно число c₀, которое принадлежит всем отрезкам последовательности. Это число удовлетворяет неравенствам: и значит оно находится среди чисел : x₁, x₂,_… .

Пусть число c₀ имеет в последовательности x₁, x₂,_… номер k, т.е. c₀= x_k. Так как c₀= x_k, то c_k по построению последовательности отрезков. С другой стороны, c₀ есть общая точка всех отрезков последовательности отрезков и значит, c₀ . Полученное противоречие показывает, что сделанное допущение неверно и что множество есть несчетное множество. Теорема доказана.

 

5. Теорема о мощности множества всех подмножеств данного множества.

 

Конечное множество состоит из конечного числа эпементов, пусть их М штук.
Подмножеств, состоящих из 1 эл-та, будет М штук, из 2 эл-тов - число
сочетаний из М по 2, по 3 эл-та - будет число сочетаний из М по 3, и т. д.
Сюда еще включают "несобственные подмножества", а именно, пустое, и
всё множество А.
Всего получится сумма С(М,0)+С(М,1)+С(М,2)+...+С(М,М).
Известно, что такая сумма равна 2^M.

Примечание: Этот факт следует из формулы бинома Ньютона, так
как (1+1)^M=2^M.

 

6. Декартово произведение, бинарное отношение.

 

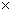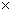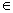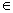Декартовым произведением множеств А и В называется множество пар, первая компонента которых принадлежит множеству А, вторая множеству В. Обозначают АВ. Таким образом АВ = {(x;y) | xA, yB}.

Операцию нахождения декартового произведения множеств А и В называют декартовым умножением этих множеств.

 

Количество пар в декартовом прoизведении А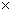В будет равно произведению числа элементов множества А и числа элементов множества В: n(А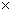В)=n(A)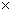n(B).

В математике рассматривают не только упорядоченные пары, но и наборы из трех, четырех и т.д. элементов. Такие упорядоченные наборы называют кортежами.

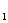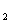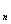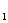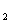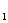
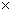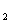
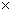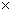Декартовым произведением множествА, А,…, A называют множество кортежей длины n, образованных так, что первая компонента принадлежит множеству А, вторая – А, …, n-ая – множеству А: АА…A.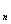

 

Бинарным отношением между двумя множествами называется соответствие элементов одного из

них элементам второго.

 

Пусть даны два множества 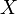и 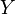, и пусть 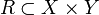- подмножество их декартова

произведения. Тогда тройка называется бинарным отношением

 

между 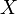и 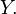Утверждение 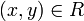обычно записывается в виде и читается "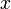 соотносится

 

с 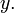" Если 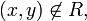то пишут 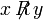или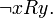

 

Бинарное отношение называется

 

инъективным, если

 

 

полным слева, если

 

 

сюръективным (или полным справа), если

 

 

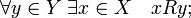
функциональным, если

 

 

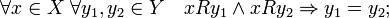
функцией, если оно полно слева и функционально;

 

биективным, если оно полно слева и справа, а также инъективно и функционально.

 

7. Иррациональность числа корень квадратный из 2.

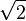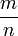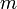Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и 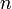— целые числа. Возведём предполагаемое равенство в квадрат:

.

Отсюда следует, что чётно, значит, чётно и 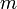. Пусть 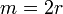, где целое. Тогда

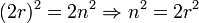
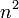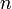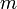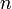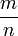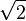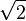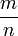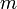Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число. Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и 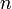— целые числа. Возведём предполагаемое равенство в квадрат:

.

Отсюда следует, что чётно, значит, чётно и 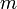. Пусть 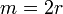, где целое. Тогда

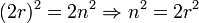
Следовательно, 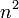чётно, значит, чётно и 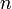. Мы получили, что 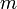и 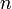чётны, что противоречит несократимости дроби 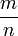. Значит, исходное предположение было неверным, и 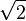— иррациональное число.

 

8. Десятичные дроби, рациональные и иррациональные числа, свойство полноты действительных чисел.

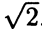
Десятичная дробь есть результат деления единицы на десять, сто, тысячу и т.д. частей. Эти дроби очень удобны для вычислений, так как они основаны на той же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями фактически те же, что и для целых чисел. При записи десятичных дробей нет необходимости отмечать знаменатель, это определяется местом, которое занимает соответствующая цифра. Сначала пишется целая часть числа, затем справа ставится десятичная точка. Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т.д. Цифры, расположенные после десятичной точки, называются десятичными знаками.

Свойства десятичных дробей.

 

1. Десятичная дробь не меняется, если справа добавить нули:

 

 

2. Десятичная дробь не меняется, если удалить нули, расположенные

в конце десятичной дроби:

Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом. Период записывается в скобках.

Свойство полноты. Для любых действительных чисел a и b (∀a∈A ∧ ∀b∈B) справедливо одно из трёх: a = b (b = a), a > b (b < a), a < b (b > a)

 

9. Ограниченные множества; точные границы и их свойства.

 

Говорят, что множество X ⊂ R ограничено сверху, если существует число c ∈ R такое, что x c для любого x ∈ X. Число c при этом называется верхней границей множества X. Аналогично определяются ограниченность множества снизу и нижняя граница множества X. Множество, ограниченное и сверху, и снизу, называется

ограниченным.

 

Рассмотрим произвольное множество действительных чисел. Если состоит из конечного числа элементов, то в имеется наименьшее число 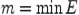и наибольшее число . Однако для бесконечных множеств наибольшие и наименьшие элементы не всегда существуют. Рассмотрим примеры:

;

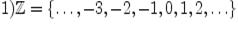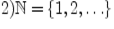
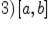
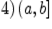
Множество не имеет наименьшего и наибольшего элементов. Интервал 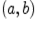тоже не имеет наименьшего и наибольшего элементов (хотя это множество ограничено), так как каково бы ни было число 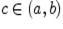, всегда найдутся 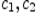такие, что 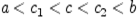. Множество 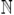не имеет наибольшего элемента, но имеет наименьший элемент . Очевидно, 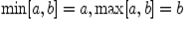, в 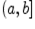нет наименьшего элемента.

Однако для бесконечных множеств, в которых нет наибольшего элемента, может существовать верхняя граница, которую нельзя уменьшить.

Множество 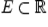называется ограниченным сверху, если существует число 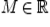такое, что для всех 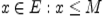. Число называется верхней границей (мажорантой) множества .

Точной верхней границей множества 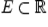называется число 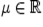такое, что

1) (т.е. -- одна из верхних границ множества );

2) (т.е. границу 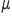множества нельзя уменьшить).

Точная верхняя граница множества обозначается
. Аналогично определяется точная нижняя граница множества, которую обозначают :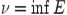

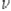1) (т.е. -- одна из нижних границ множества );

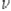2) (т.е. границу множества нельзя увеличить).

Определение Точная верхняя граница множества 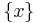это его наименьшая верхняя граница. Точная верхняя граница обозначается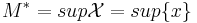

Определение Точная нижняя граница множества 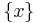это его наибольшая нижняя граница Точная нижняя граница обозначается

 

 

10. Теорема существования точной верхней (нижней) границы для ограниченного сверху (снизу) множества.

 

Если множество 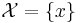ограничено сверху (снизу) то существует его точная верхняя (нижняя) граница

Доказательство:

Рассуждения будут проводится в отношении верхней границы. Разобьем на два случая

1) Среди чисел 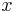множества 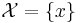существует наибольшее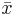

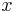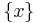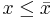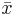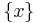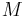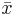Тогда для любого числа из множества , , значит является верхней границей множества . С другой стороны для любой верхней границы должно выполнятся , а значит является наименьшей из границ, т.е. точной верхней границей

2) Среди чисел 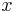множества 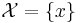не существует наибольшего

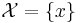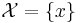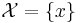Произведем сечение в области вещественных чисел К верхнему классу отнесем все верхние границы множества , к нижнему классу отнесем все остальные вещественные числа. Легко видеть что такое разбиение действительно является сечением Т.к. все вещественные числа распределены и любое число в больше любого числа в . При этом все числа из множества попадут в , т.к. в множестве нет наибольшего числа.(Если бы 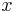попал в , то он значит был бы верхней границей, а значит был бы наибольшим, что противоречит допущению) По основной теореме Дедекинда должно существовать вещественное число 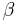производящее сечение. Очевидно что 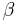является верхней границей множества 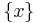, также очевидно, что 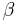является точной верхней границей.

Основная теорема (Дедекинда) Для всякого сечения в области вещественных чисел существует вещественное число 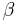которое производит это сечение. Это число 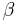будет либо наибольшим в нижнем классе , либо наименьшим в верхнем классе