Второй замечательный предел

Рассмотрим числовую последовательность , где 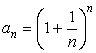, 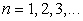С ростом основание степени уменьшается до единицы, а показатель растет до бесконечности, поэтому ничего конкретного о поведении 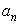сказать нельзя. Для вычисления 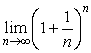воспользуемся выражением для бинома Ньютона:

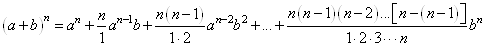. (0.0.1)

В нашем случае

.

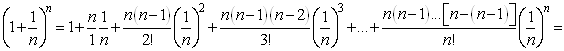
Из полученного выражения следует, что с увеличением величина 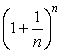растет. Действительно, перейдем от к . Это приведет к тому, что число слагаемых возрастет на одно. Кроме того, величина множителей, заключенных в скобки, тоже возрастет, так как 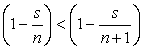. Но если увеличивается число слагаемых и сами слагаемые растут, то 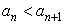. Значит, числовая последовательность монотонно возрастает.

Докажем теперь, что данная последовательность ограничена сверху. Заменим все скобки вида 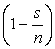единицей. Так как 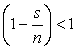, то

.

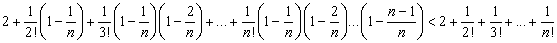Кроме того , ,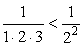..., . 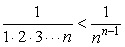Значит,

.

В правой части неравенства после цифры 2 стоит убывающая геометрическая прогрессия. Как известно, сумма первых членов такой прогрессии равна: 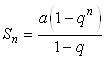. В нашем случае 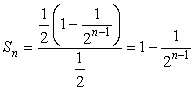. С ростом величина 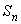будет, очевидно, стремится к единице. Значит, 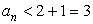, то есть, ограничено сверху.

Итак, мы получили, что 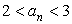. Но так как монотонно возрастающая последовательность ограниченная сверху, то она имеет предел:

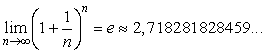
Можно доказать, что данный предел справедлив не только для натуральных чисел, но и для любых значений :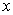

.

Полученное выражение и называется вторым замечательным пределом.

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, т.е. докажем, что 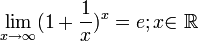. Рассмотрим два случая:

1. Пусть 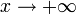. Каждое значение x заключено между двумя положительными целыми числами: 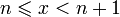, где n = [x] - это целая часть x.

Отсюда следует: , поэтому

.

Если 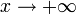, то 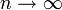. Поэтому, согласно пределу 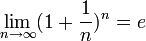, имеем:

.

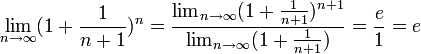
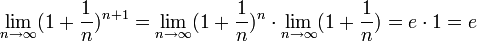По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку − x = t, тогда

.

Из двух этих случаев вытекает, что 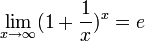для любого x.