рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Матрицы. Действия над ними
Реферат Курсовая Конспект
Матрицы. Действия над ними
Матрицы. Действия над ними - раздел Математика, 1. Матрицы. Действия Над Ними. Опр1. Матрицей A Размерности S...
1. Матрицы. Действия над ними.
Опр1. Матрицей A размерности Sxn называется прямоугольная таблица из чисел, состоящая из S строк и n столбцов.

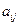 - элемент матрицы,
- элемент матрицы,
i – номер строки,
j – номер столбца.

Типы матриц:
1.  квадратная матрица;
квадратная матрица;
2. 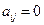
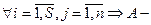 нульматрица;
нульматрица;
3.  ; A – диагональная матрица
; A – диагональная матрица  элементы главной диагонали.
элементы главной диагонали.
4.  единичная матрица.
единичная матрица.
5. 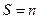
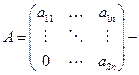 верхняя треугольная матрица.
верхняя треугольная матрица.
6. 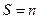
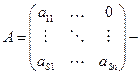 нижняя треугольная матрица
нижняя треугольная матрица
Определение2 Пусть матрицы А и В имеют одинаковую размерность, тогда 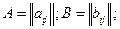
Пусть 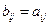 для
для  , тогда говорят, что матрицы А и В равны: А=В.
, тогда говорят, что матрицы А и В равны: А=В.
Определение3 Пусть матрицы А и В имеют одинаковую размерность, 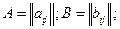 тогда суммой матриц А и В называется матрица
тогда суммой матриц А и В называется матрица 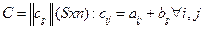
С=А+В;
Определение4 Пусть 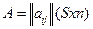 , а
, а 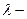 вещественное число, тогда произведением матрицы А на число
вещественное число, тогда произведением матрицы А на число 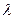 называется матрица
называется матрица 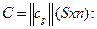

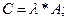
Свойства линейных операций над матрицами
Перестановочность:
1. А+В=В+А
2. (А+В)+С=А+(В+С);
Распределительный закон умножения
3.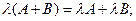
4. 
5. 
Определение5 Пусть существуют матрицы
С – разность А и В, если можно записать А=В+С; обозначается С=А-В.
Определение6 Пусть матрицы 
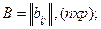
Матрица 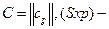 называется произведением матриц А и В (обозначается С=АВ), если
называется произведением матриц А и В (обозначается С=АВ), если
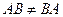
Определение7 Транспонированная матрица. Транспонировать матрицу А значит записать столбцы матрицы А строками с теми же номерами.
значит записать столбцы матрицы А строками с теми же номерами.
2. Перестановки, подстановки. Понятие инверсии и четности.
Опр1. Перестановкой n-го порядка называется упорядоченная последовательность 
 элемент перестановки элементов множества М.
элемент перестановки элементов множества М.
Запишем все перестановки n=3 M={1,2,3}

6 – различных перестановок 3-го порядка
Утверждение существует n! различных перестановок n-го порядка.
Опр2 Говорят что элементы  и
и 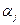 образуют беспорядок(инверсию) в перестановке, если
образуют беспорядок(инверсию) в перестановке, если 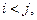 но при этом
но при этом  .
.
Пример  всего 5 инверсий N(4312)=5.
всего 5 инверсий N(4312)=5.
Опр3. Транспонизацией элементов и
и 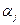 называется перемена их местами при этом все остальные элементы фиксированы.
называется перемена их местами при этом все остальные элементы фиксированы.
Утверждение Любая транспонизация элементов меняет четность перестановки.
Опр4. Подстановкой n-го порядка называется однозначное отображение множества M
Это отображение записывается в виде  ;
;
Если N(p) – чётное(нечётное) число, то подстановка p называется чётной(нечётной).
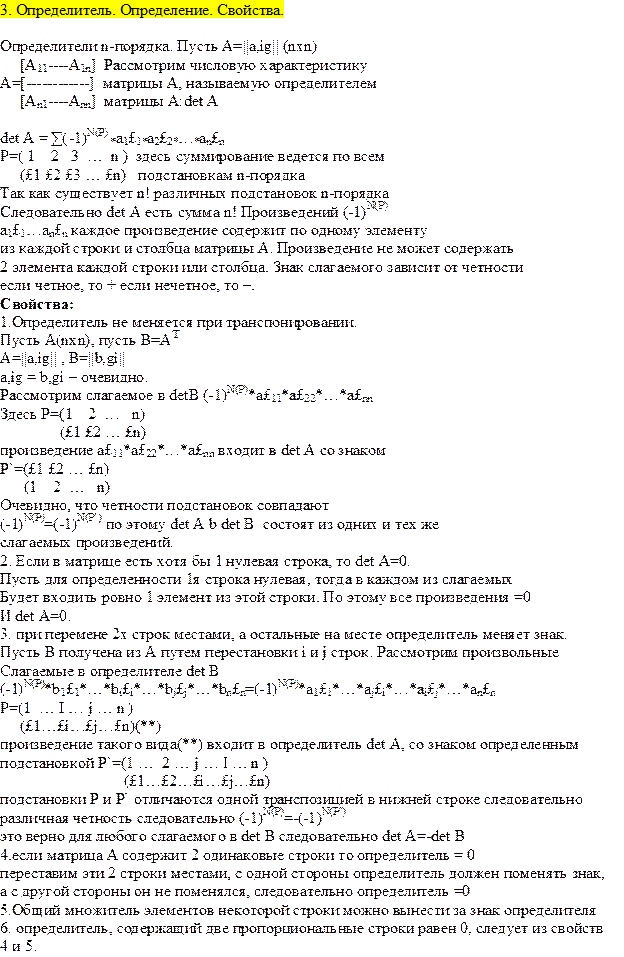

5. Линейная зависимость системы столбцов. Ранг матрицы. Теорема о ранге матрицы и ее следствие (необходимое и достаточное условие равенства нулю определителя). Базисный минор.
Пусть матрица A=||aij|| (mxn)
Обозначим B1,B2,..,Bk – столбцы матрицы A
Определение: Столбцы B1,..,Bk называются линейно зависимыми, если существуют числа 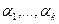 , такие, что
, такие, что 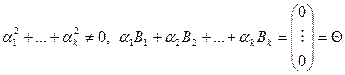
Определение: Столбцы B1,…,Bk называются линейно независмыми, если равенство выполняется тогда и только тогда, когда α1=α2=αk=0.
Утверждение: Столбцы B1,…,Bk линейно зависимы тогда и только тогда, когда хотя бы один из них является линейной комбинацией других столбцов. Т.е. например, B1=α2B2+…+αkBk.
Определение: Ранг матрицы A – максимальный порядок неравного нулю минора.
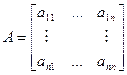 Обозначается: RangA, r(A).
Обозначается: RangA, r(A).
Замечание:
1) RangA=0, 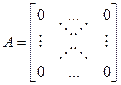
2) Очевидно, что если в матрице все миноры k-го порядка равны 0, то равны нулю все миноры большего порядка. Поэтому, для вычисления ранга матрицы, необходимо вычислять миноры, повышая порядок.
Пример:
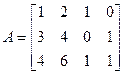 ; det(1)=1≠0
; det(1)=1≠0 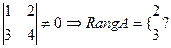
 ;
;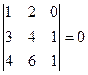 ;
; ;
;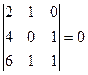
RangA=2.
Определение: Минор, определяющий ранг матрицы, называется базисным. Строки и столбцы, формирующий базисный минор, называются базисными строками и столбцами.
Теорема (о базисном миноре): Базисные строки (столбцы) линейно независимы. Остальные строки (столбцы) являются линейными комбинациями базисных строк (столбцов).
Доказательство: Для столбца B
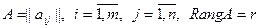
Пусть для определенности базисный минор (минор порядка r(≠0)) расположен в верхнем левом углу. Этот минор равен D≠0; все миноры порядка выше r равны нулю. 
Предположим, что базисные столбцы линейно зависимы. Тогда бы базисный минор состоял из столбцов, один из которых является линейной комбинацией остальных столбцов в D (см. утверждение). Тогда в силу свойств определителя D=0 – пришли к противоречию => базисные столбцы линейно независимы. Докажем, что другие столбцы есть линейная комбинация базисных столбцов. Докажем это для l-того столбца 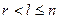 . Рассмотрим вспомогательные определители порядка (r+1) вида:
. Рассмотрим вспомогательные определители порядка (r+1) вида:

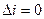 для
для 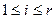 т.к. две одинаковые строки
т.к. две одинаковые строки
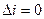 для
для 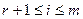 т.к. в этом случае
т.к. в этом случае 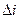 есть минор (r+1) порядка у матрицы A rangk<n
есть минор (r+1) порядка у матрицы A rangk<n
Выпишем разложение определителей 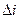 по i-той строке:
по i-той строке:

Алгебраические дополнения A1,…,Ar не зависят от индекса:
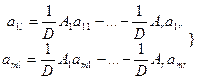 m равно B
m равно B
 => l-тый (l>r) есть линейная комбинация базисных столбцов B1,…,Br с коэффициентами
=> l-тый (l>r) есть линейная комбинация базисных столбцов B1,…,Br с коэффициентами 
Теорема (о ранге матрицы): Ранг матрицы равен максимальному числу линейно независимых строк (столбцов).
Доказательство: Докажем для столбцов. Пусть RangA=r. Надо доказать, что r=k, где k – максимальное число независимых столбцов любого множеств, состоящего из больше, чем k столбцов.
Предположим, что k<r. Это невозможно, т.к. существует к линейно независимых базисных столбцов. Следовательно R≥r.
Предположим, что k>r. Докажем, что это невозможно.
Пусть столбцы C1,…,Ck – линейно независимы. Обозначим B1,…,Bk – базисные столбцы (может быть, некоторые из столбцов C совпадают с столбцами B). Каждый из столбцов C1,…,Ck может быть записан в виде линейной комбинации базисных столбцов:
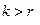
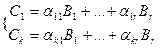
Составим некоторую линейную комбинацию из столбцов. Тогда достаточно будет выражения равенства:
 матричное равенство. m уравнений в правой части – 0, относительно k неизвестных β1,…,βk, k>m
матричное равенство. m уравнений в правой части – 0, относительно k неизвестных β1,…,βk, k>m
При рассмотрении метода Гаусса докажем, что  ненулевое решение
ненулевое решение 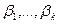 такой системы. Т.е.
такой системы. Т.е.
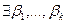 не все равны нулю:
не все равны нулю:  . Но это противоречит предположению о линейной независимости столбцов C1,…,Ck
. Но это противоречит предположению о линейной независимости столбцов C1,…,Ck
Вывод: k<r – невозможно, k>r – невозможно, следовательно, k=r.
Следствия:
1. Определение: Ранг матрицы можно определить как максимальное число линейно независимых строк (столбцов).
2. Необходимым и достаточным условием равенства нулю определителя:
Пусть A: nxn, если detA=0 ó RangA<n
Доказательство:
Достаточно: RangA<n => n столбцов линейно зависимы => detA=0
Необходимо: Пусть detA=0 => базисный минор не может иметь порядок n => RangA<n.
Замечание: В доказательстве теоремы о базисном миноре мы рассматривали только минор, содержащий в себе базисный минор. Этого оказалось достаточным, чтобы гарантировать, что RangA=r.
6.Обратная матрица, Необходимое и достаточное существование обратной матрицы
Вырожденная матрица.
Пусть А-квадратная матрица nxn Матрица B(C) называется левая(правая) обратная матрица к А, если выполнено равенство B*A=E (A*C=E)
Пусть существуют левая и правая обратные матрицы В и С, тогда В=С
В=В*Е=В*(А*С)=(В*А)*С=Е*С=С
Существуют правая и левая обратные матрицы, тогда в силу того что В=С=А^(-1)
A-1*A=A*A-1=E
Пусть det A не равен 0 тогда если обратная матрица существует то det A-1=1/det A
Det(A*A-1)=det E=1
Det A*det A-1=1
detA-1=1/det A
квадратная матрица А называется невырожденной если определитель не равен 0
вырожденная если определитель равен 0.
Обратная матрица существует тогда и только тогда когда матрица А невыродженная
Необходимость.
Пусть существует А^(-1) тогда А невыродженная.
Если есть А^(-1) то det(A*A^(-1))=det A*det A^(-1)=1
Det A не равен 0
Достаточность.
Пусть det A не равен 0 то есть A^(-1)
Рассмотрим В=1/det A[A11 A21…An1] 1/det A[A11……A1n](T)
[A12 A22…An2]= [A21……A2n]
[A1n A21n..Ann] [An1……Ann]
докажем что В является левой обратной к А.
вычислим А*В
1/det A[A11 A21….An1] [a11 a1j a1n]
[A1i A2i…...Ani] [a21 a2j a2n]=C
[A1n A21n..Ann] [an1 anj ann]
Cij=1/detA(A1i*a1j+…+Ani*anj)=1/det A*det A*δij(1,i=g|0,i≠g) следовательно С=E
B есть левая обратная к А, аналогично что В является правой обратной к А.
A^(-1)=(1/det A)*(A(v))(T)
A(v)-союзная матрица из алгебраических дополнений.
7. Линейное векторное пространство. Определение, примеры.
Опр.
Множество L элементов любой природы называется линейное пространство, если
1). В это множестве введена операция сложения элементов, не выходящих за пределы L.
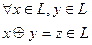
2).Введена операция умножения на вещественное число: 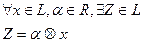
3). Операция плюс, умножение на вещественное число обладают 8 свойствами(аксиомами линейного пространства):
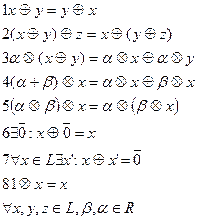
Замечание.
1 Если в определение множества пространства идет речь об умножении на вещественное число, то такое линейное пространство называется вещественным линейным пространством. Существуют комплексные множества пространства.
2 Элементы линейного пространства называют векторами.  Нулевой вектор.
Нулевой вектор.
Утверждение 1. Нулевой элемент единственный.
Доказательство.
Пусть существуют два нулевых элемента 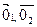 тогда
тогда 
Утверждение 2. Противоположный элемент единственен.
Доказательство от противного. Пусть 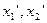 противоположные к элементу X.
противоположные к элементу X.
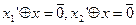

Определение. Пусть 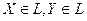 Элемент
Элемент  называется разностью X-Y, если
называется разностью X-Y, если 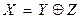 Очевидно
Очевидно
Примеры линейных пространств.
1 Множество векторов- направленных отрезков, если ввести + по правилу треугольника, а умножение на число так, как это было сделано в школе- есть линейное пространство, т.е выполняется восемь аксиом линейного пространства.
2 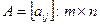
 так как это было сделано раньше.
так как это было сделано раньше.
8 аксиом выполняются
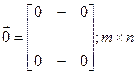
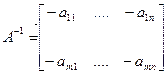
3.Множество многочленов степени не выше n.  с вещественными коэффициентами.
с вещественными коэффициентами.
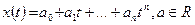
 -обычным образом. 8 аксиом.
-обычным образом. 8 аксиом.

 -линейное пространство.
-линейное пространство.
4 Множество непрерывных функций на  .
.
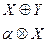 - обычным образом.
- обычным образом. 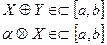 Аксиомы 1-8 выполнены.
Аксиомы 1-8 выполнены. 
С линейное пространство.
линейное пространство.
5.L={0}-нуль пространства.
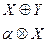 -как обычно. Аксиомы 1-8-выполнены.
-как обычно. Аксиомы 1-8-выполнены.
Замечание.
В одном и том же множестве вводить 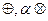 можно разными способами лишь бы только выполнялись 8 аксиом. При этом будут получаться различные линейные пространства.
можно разными способами лишь бы только выполнялись 8 аксиом. При этом будут получаться различные линейные пространства.
Контр примеры.
1. Пусть L-множество многочленов степени n. 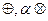 -как обычно.
-как обычно.
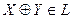 -вообще говоря, неверно. Например
-вообще говоря, неверно. Например 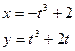
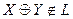 (n=3).
(n=3).
2. L-множество векторов на плоскости, параллельных либо 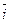 либо
либо 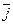 .
.
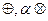 -как обычно.L-не является линейным пространством, т.к. нет замкнутости относительно
-как обычно.L-не является линейным пространством, т.к. нет замкнутости относительно 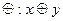 не обязательно принадлежит L.
не обязательно принадлежит L.
Замечание.
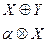
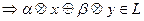
8. Линейная зависимость и независимость векторов в линейном пространстве. Базис в линейном пространстве. Координаты вектора в базисе.
Базис в линейном пространстве.
Опр1. Пусть 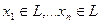 .L-линейное пространство. Сумма вида
.L-линейное пространство. Сумма вида  называется линейной комбинацией векторов
называется линейной комбинацией векторов 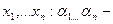 коэффициенты линейных комбинаций.
коэффициенты линейных комбинаций.
Опр2. Элементы 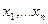 линейного пространства L называются линейно зависимыми, если
линейного пространства L называются линейно зависимыми, если 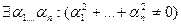
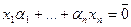 в противном случае
в противном случае  линейно независимы.
линейно независимы.
Опр3 Элементы 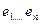 линейного пространства L образуют базис, если 1)
линейного пространства L образуют базис, если 1) 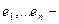 линейно зависимы;2)
линейно зависимы;2) 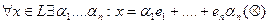 последнее равенство разложение элемента x по базису
последнее равенство разложение элемента x по базису 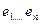 числа.
числа. 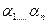 -координаты вектора x в базисе
-координаты вектора x в базисе 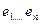 .
.
Утверждение 1
Пусть  -линейно зависимые вектора, тогда один из них выражается в виде линейной комбинации других.
-линейно зависимые вектора, тогда один из них выражается в виде линейной комбинации других.
Доказательство.
 -линейно зависимые.
-линейно зависимые. 
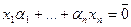 пусть
пусть 
Утверждение 2
Пусть хотя бы один из элементов 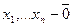 тогда система
тогда система  линейно зависимая.
линейно зависимая.
Доказательство.
Пусть для определенности 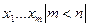 линейно зависимые вектора. Составим линейную комбинацию вида
линейно зависимые вектора. Составим линейную комбинацию вида 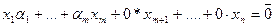
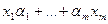 можно сделать равной 0 подобрав
можно сделать равной 0 подобрав 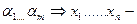 линейно зависимые.
линейно зависимые.
Теорема1
Координаты вектора в базисе определяется однозначно.
Доказательство
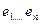 -базис в L
-базис в L  Предположим, что сущ. два разложения элемента x по базису e:
Предположим, что сущ. два разложения элемента x по базису e:
 но вектора
но вектора  -линейно независммы(т.к. e-базис)
-линейно независммы(т.к. e-базис)

Следствие.
Два элементы линейного пространства равны между собой (совпадают). Т. и т. т.к совпадают их соответственные координаты в одном и том же базисе.
Теорема 2
При сложении элементов линейного пространства их соответствующие координаты складываются. При умножение элемента на число его координаты умножаются на это число.
Теорема 3
Пусть 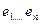 -базис в линейном пространстве L, тогда любая система из большого, чем n, числа векторов- линейно зависимы.
-базис в линейном пространстве L, тогда любая система из большого, чем n, числа векторов- линейно зависимы.
Доказательство
Рассмотрим производную систему m>n числа векторов 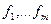 . Разложим каждый вектор f по базису e:
. Разложим каждый вектор f по базису e:
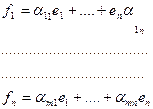 напишем некоторые линейную комбинацию
напишем некоторые линейную комбинацию 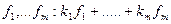 докажем, что
докажем, что 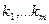 можно подобрать так, что такая линейная комбинация =
можно подобрать так, что такая линейная комбинация =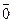 .
.
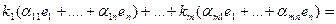
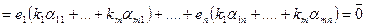
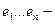 линейно зависимые =необходимо
линейно зависимые =необходимо
 из n уравнений относительно m неизвестных m>n
из n уравнений относительно m неизвестных m>n
Такая система уравнений имеет нетривиальное(т.е. не нулевое) решение
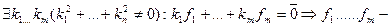 линейно зависимы
линейно зависимы
Теорема4
Все базисы в линейном пространстве L состоят из одного и того же числа векторов.
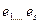 (базис)
(базис)  (базис)
(базис)
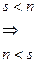 не может быть
не может быть
Опр4
Размерностью линейного пространства называется число векторов в базисе.
Опр5
Пространство называется бесконечномерным, если для любого n существует система из n линейно независимых векторов.
9.Размерность линейного пространства.
Определение:Размерностью линейного пространства называется число векторов в базисе dimL=n.
Определение:пространство L называется бесконечно мерным,если 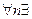 система из n линейно независимых векторов
система из n линейно независимых векторов 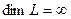
Примеры
1.Трехмерное пространство векторов - направленных отрезков. Любая тройка некомпланарных векторов образует базис. dimL=3
2.Пространство векторов-направленных отрезков на плоскости. Базис – любая пара неколлинеарных векторов на этой плоскости. dimL=2
3.L-пространство строк длины n. 
Докажем,что это линейно независимая система:
1). -линейно независимы
-линейно независимы
2).Очевидно,что 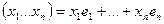 .
.
Из второго и первого следует, что 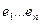 -базис пространства: dimL=n
-базис пространства: dimL=n
4.Пространство многочленов степени не выше n 

Докажем,что это базис:
1)
В силу основной теоремы алгебры многочлен n-ой степени не может иметь больше чем n корней, следовательно уравнение выполняется только при 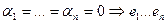 -линейно независимы.
-линейно независимы.
2)Очевидно, что любой многочлен степени <= n может быть записан в виде линейной комбинации 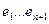
Из первого и второго следует,что 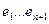 -базис, dimL=n+1
-базис, dimL=n+1
5.C[a,b]- пространство функций, непрерывных на [a,b]. 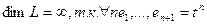 -(n+1) функция из этого пространства C[a,b], причем
-(n+1) функция из этого пространства C[a,b], причем 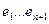 -линейно независимы по основной теореме.
-линейно независимы по основной теореме.
10.Переход к новому базису.Матрица перехода.Преобразование координат вектора при переходе к новому базису.
L,dimL=n
 -“старый” базис
-“старый” базис
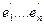 -“новый” базис
-“новый” базис


Определение: Матрица  называется матрицей перехода от e к e’.j-тый столбец в матрице перехода
называется матрицей перехода от e к e’.j-тый столбец в матрице перехода  состоит из координат вектора
состоит из координат вектора  в старом базисе
в старом базисе

Формально:
Формально:
Аналогично:
Теорема:Матрица перехода невырождена.
Доказательство:
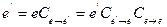
Т к базисы состоят из линейно независимых векторов, то обязательно 
Рассмотрим 
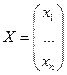
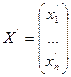
Формально x=eX=e’X’=e X’.В силу линейной независимости
X’.В силу линейной независимости  ,получаем,что X=
,получаем,что X= X’.Домножим слева на
X’.Домножим слева на 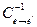 и получим X’=
и получим X’=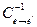 X
X

11. Правило Крамера для решения систем линейных алгебраических уравнений.
Пусть А = 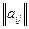 (n
(n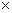 n) ; X =
n) ; X =  ; B =
; B =  ;
;
(1) AX = B
Теорема Крамера:
Система (1) имеет решение (и притом одно единственное) если detA 0
0
Доказательство:
detA 0
0 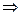

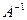 ; умножим систему (1) на
; умножим систему (1) на 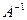
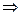 (
(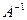 А)Х =
А)Х = 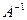 В
В 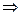 ЕХ =
ЕХ = 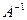 В
В
Х =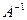 В
В
Т.е., если detA 0, то всегда
0, то всегда  решение Х =
решение Х = 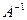 В
В
Докажем, что это решение единственное. Пусть Y — другое решение.

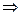 AX = AY; Умножим на
AX = AY; Умножим на 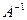 , получим что X = Y.
, получим что X = Y.
Формула Крамера (вывод).
Х =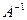 В =
В =  =
= 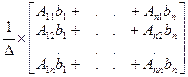 =
= 
 = detA
= detA

X = , где
, где 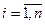 — формула Крамера (правило Крамера)
— формула Крамера (правило Крамера)
Замечания
1. detA 0 не является условием совместимости системы
0 не является условием совместимости системы
Пример: 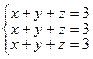 detA = 0
detA = 0
2. Для больших n применение правила Крамера нецелесообразно, т.к. необходимо вычислить n+1 определитель n-го порядка. Необходимо использовать другие методы (метод Гауса).
12. Системы линейных уравнений. Теорема Кронекера-Капелли.

Числа  называются коэффициентами системы;
называются коэффициентами системы;
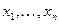 — неизвестные;
— неизвестные; 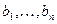 — свободные члены;
— свободные члены;
 (
(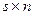 );
); 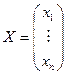 ;
;  ;
;
(1) AX = B — матричная запись
Опр1: Упорядоченная совокупность вещественных чисел 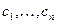 называется решением системы (1), если при подстановке в уравнения получаются верные равенства.
называется решением системы (1), если при подстановке в уравнения получаются верные равенства.
Опр2: Система (1) называется совместной, если имеет хотя бы одно решение.
Опр3: Система (1) называется определенной, если она имеет ровно одно решение и называется неопределенной, если имеет более одного решения.
Решить систему (1) значит:
1) Установить совместность;
2) Если она определенная, найти её единственное решение;
3) Если неопределенная, то описать все множество решений.
Теорема Кронекера-Капелли
Теорема: Система (1) совместна , — расширенная матрица Доказательство:Линейная зависимость векторов.
Опр2:Система в-в назыв. линейно зависимой, если () =. В противном случае система явл. линейно независимой. Утв1(док-во самостоят):Система векторов линейно зависимо один из векторов выражается в виде лин. комбинации других. …Базисы на прямой, на плоскости, в пространстве.
Опр2.Два линейно независимых вектора , лежащие в плоскости P, называются базисом на плоскости Р, если вектор , лежащий на плоскости Р можно записать… Опр3.Три линейно независимых вектора называются базисом в пространстве, если… ТеоремаДоказательство
Док-во 3го свойства: ([a+b,c],d)=(a+b,[c,d])=(a,[c,d])+(b,[c,d])=… 21.Смешанное произведение векторов и его свойства.Необходимое и достаточное условия компланарности векторов.N _Axo+Byo+Czo+D=0
Ax+By+Cz+D=0
⇕ (n,MoM)=0 n={A,B,C},M(x,y,z)-произвольная точка.– Конец работы –
Используемые теги: матрицы, действия, над, ними0.074
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Матрицы. Действия над ними
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов