рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Реферат Курсовая Конспект
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ - раздел Математика, Министерство Образования Российской Федерации Воронежский Государств...
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Пособие для студентов по специальностям 010100 и 510100
ВОРОНЕЖ
Утверждено научно-методическим советом математического
факультета ( 2 сентября 2003г., протокол №2 )
Составители: Михайлова И. В.
Баркова Л. Н.
Пособие подготовлено на кафедре уравнений в частных производных и теории вероятностей математического факультета Воронежского государственного университета.
Рекомендуется для студентов 3 курса дневного и 5 курса вечернего отделений.
§1. Элементы комбинаторики.
Центральной задачей комбинаторной теории (комбинаторики) можно считать задачу размещения (распределения) объектов в соответствии со специальными правилами. Если эти правила просты, то основным в этой задаче является подсчет числа возможностей для осуществления искомого размещения. Задачи такого типа принято называть задачами перечисления. Если же правила распределения объектов сложны, то главной проблемой становится вопрос существования таких распределений и нахождения методов их осуществления.
Нас будут интересовать только перечислительные задачи. В том случае, когда интересующих нас вариантов размещения немного, мы можем все эти варианты перебрать. В других случаях это невозможно из-за большого числа вариантов и тогда на помощь приходят основные правила подсчета: принципы
(правила) сложения и умножения.
Принцип суммы. Пусть множество А содержит п элементов, а множество B - k элементов, причем 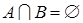 . Тогда множество
. Тогда множество 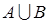 содержит п + k элементов.
содержит п + k элементов.
Замечание 1. Если обозначить  - число элементов множества А, то в формализованном виде правило суммы можно сформулировать следующим образом: если
- число элементов множества А, то в формализованном виде правило суммы можно сформулировать следующим образом: если 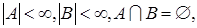 то
то  .
.
Замечание 2. При решении задач удобной бывает следующая формулировка: элемент из А или элемент из В можно выбрать п+ k числом способов, где п - количество способов выбрать элемент из А, k – элемент из В .
Принцип произведения. Пусть заданы два множества  и
и . Тогда декартово произведение
. Тогда декартово произведение
 содержит
содержит  элементов, т.е.
элементов, т.е.  , если
, если 
Подводя итог сказанному, подчеркнем, что если выбирается или то или другое, то нужно применять правило суммы, а если и то, и другое, то правило произведения. Например, на тарелке лежат 5 яблок и 3 груши. Если выбираем яблоко или грушу, то число способов 5+3=8. Если выбираем и яблоко, и грушу, то 5 • 3 == 15.
Замечание 1. Пусть необходимо выполнить одно за другим какие-то  действий (
действий (
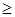 2). Если первое действие можно выполнить
2). Если первое действие можно выполнить  способами, после чего второе
способами, после чего второе 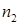 способами, после чего и т.д.
способами, после чего и т.д.  - ое действие можно выполнить
- ое действие можно выполнить 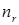 способами, то все
способами, то все  действий можно выполнить
действий можно выполнить 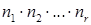 способами.
способами.
Замечание 2.Если на выполнение какого-либо из действий наложены ограничения (т.е. некоторое действие необходимо выполнить по-особому, не так, как другие), то обычно бывает целесообразно подсчет начинать именно с этого действия.
Пример. В автомашине семь мест. Сколькими способами семь человек могут сесть в эту машину, если занять место водителя могут только трое из них?
Решение. Для размещения семи человек в автомашине необходимо выполнить семь действий (заполнить семь мест), то есть  = 7. На одно из этих действий (заполнение места водителя) наложены ограничения. Поэтому это действие будем считать первым и тогда
= 7. На одно из этих действий (заполнение места водителя) наложены ограничения. Поэтому это действие будем считать первым и тогда  = 3, после чего заполнение любого из оставшихся можно осуществить
= 3, после чего заполнение любого из оставшихся можно осуществить 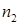 = 6 способами и т.д. Заполнение последнего места можно выполнить только одним способом, то есть
= 6 способами и т.д. Заполнение последнего места можно выполнить только одним способом, то есть  = 1. Согласно принципу умножения, все семь действий можно выполнить 3
= 1. Согласно принципу умножения, все семь действий можно выполнить 3 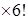 способами.
способами.
Принципы умножения и сложения дают нам общий метод решения задач. Помимо этого общего метода, полезными оказываются следующие понятия и формулы.
Рассмотрим сначала следующую задачу. Из трех букв 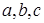 нужно выбрать какие-то две. Сколько способов выбора? Оказывается здесь спрятаны четыре задачи.
нужно выбрать какие-то две. Сколько способов выбора? Оказывается здесь спрятаны четыре задачи.
Считать ли ab и 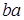 одинаковыми вариантами? Если порядок выбора существенен, то варианты выбора будем называть размещениями. Если порядок выбора безразличен, то варианты выбора будем называть сочетаниями.
одинаковыми вариантами? Если порядок выбора существенен, то варианты выбора будем называть размещениями. Если порядок выбора безразличен, то варианты выбора будем называть сочетаниями.
Другой важный вопрос - возможны ли повторения? То есть можем ли мы выбирать два раза одну какую-либо букву? Если да, то мы говорим о размещениях или сочетаниях с повторениями, а если нет - то о размещениях или сочетаниях без повторений.
Итак, пусть  - множество произвольной природы, содержащее п элементов, n
- множество произвольной природы, содержащее п элементов, n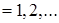 .
.
Размещениями без повторений или просто размещениями из n элементов множества В по
элементов множества В по  элементов будем называть всевозможные упорядоченные подмножества В, содержащие
элементов будем называть всевозможные упорядоченные подмножества В, содержащие  различных элементов множества В. Число размещений из n по
различных элементов множества В. Число размещений из n по 
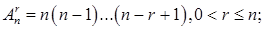 и
и 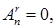 при
при 
Размещениями с повторением из п элементов множества  по
по  элементов будем называть упорядоченные наборы по
элементов будем называть упорядоченные наборы по  элементов множества
элементов множества  , среди которых могут быть и одинаковые элементы. Число таких размещений
, среди которых могут быть и одинаковые элементы. Число таких размещений
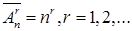 .
.
Перестановками из п элементов множества В назовем размещения из п элементов множества  по n
по n элементов. Число перестановок из п различных элементов
элементов. Число перестановок из п различных элементов  .
.
Сочетаниями из n элементов множества  по
по  элементов называются подмножества множества В, содержащие
элементов называются подмножества множества В, содержащие  различных элементов множества В. Число сочетаний из n
различных элементов множества В. Число сочетаний из n по
по 


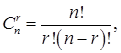

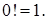
Сочетаниями с повторениями из п элементов множества В по  элементов называются всевозможные наборы, содержащие
элементов называются всевозможные наборы, содержащие  элементов множества В, среди которых могут быть одинаковые. Число сочетаний с повторениями из
элементов множества В, среди которых могут быть одинаковые. Число сочетаний с повторениями из  по
по 
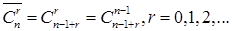 ,
, 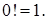
Замечания. Различные размещения из п элементов множества В по  элементов (с повторениями и без повторений) отличаются друг от друга составом (хотя бы одним из элементов) или порядком (роль элементов в размещении различна).
элементов (с повторениями и без повторений) отличаются друг от друга составом (хотя бы одним из элементов) или порядком (роль элементов в размещении различна).
Различные перестановки из n элементов множества В отличаются друг от друга только порядком следования элементов.
Различные сочетания из n элементов множества В по  элементов отличаются друг от друга только составом.
элементов отличаются друг от друга только составом.
Возвратимся к поставленной задаче и найдем число способов выбора двух букв из указанных.
В том случае, когда осуществляется выбор без возвращения выбранного элемента в исходную совокупность, т.е. речь идет о размещениях без повторений, число вариантов равно  Перечислим их
Перечислим их  .
.
Если же осуществляется выбор с возвращением, то число вариантов равно . Это -
. Это -  .
.
В другом случае, если порядок букв не существенен и буквы не повторяются, то, используя формулу сочетаний без повторений, имеем
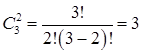 . Здесь варианты
. Здесь варианты 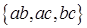 .
.
И, наконец, число сочетаний с повторениями 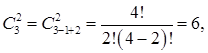 а варианты:
а варианты:  .
.
Задачи для самостоятельного решения
1. На окружности выбрано десять точек. Сколько существует хорд с концами в этих точках? Сколько ненулевых векторов с концами в этих точках? Сколько векторов с концами в этих точках? Сколько треугольников с вершинами в этих точках? Сколько выпуклых пятиугольников, выпуклых десятиугольников?
2. Даны три карточки с цифрами 1,2,3. Сколько чисел можно составить из этих трех карточек?
3. Десять спортсменов разыгрывают золотую, серебряную и бронзовую медали. Сколькими способами эти медали могут быть распределены между спортсменами?
4. Сколькими способами  девушек могут образовать хоровод?
девушек могут образовать хоровод?
5. Сколькими способами  различных шаров можно разместить по
различных шаров можно разместить по  различным ячейкам, предполагая, что а) в ячейке может быть более одного шара; в) не может быть более одного шара.
различным ячейкам, предполагая, что а) в ячейке может быть более одного шара; в) не может быть более одного шара.
6. Сколько различных подмножеств, включая само множество и пустое, можно выделить из множества, содержащего  элементов.
элементов.
7. В розыгрыше лотереи участвуют 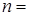 3 человека. Каждому из них присвоен порядковый номер. Участники лотереи должны вытащить одну карточку из трех с номерами 1,2,3. Призы выдаются тем, кто вытащит карточку со своим порядковым номером. Каково число вариантов, в которых выигрыш только у одного участника лотереи? В которых ни один не выигрывает? Ответить на вопросы для произвольного
3 человека. Каждому из них присвоен порядковый номер. Участники лотереи должны вытащить одну карточку из трех с номерами 1,2,3. Призы выдаются тем, кто вытащит карточку со своим порядковым номером. Каково число вариантов, в которых выигрыш только у одного участника лотереи? В которых ни один не выигрывает? Ответить на вопросы для произвольного 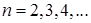
8. Сколько пятибуквенных слов (перестановок), каждое из которых состоит из трех согласных и двух гласных, можно образовать из букв слова УРАВНЕНИЕ.
§ 2. Математическая модель случайного опыта.
Пусть G - некоторый случайный опыт, обладающий свойством устойчивости частот, т.е.
опыт, результаты которого не могут быть предсказаны однозначно до проведения испытаний;
возможны повторения испытания с первоначальным комплексом исходных данных сколь угодно большое число раз;
невозможно точное предсказание результата не только первого испытания, но и каждого последующего;
при неограниченном увеличении количества проведенных испытаний частота любого исхода стабилизируется, т.е. в определенном смысле близка к некоторой постоянной, называемой в дальнейшем вероятностью исхода.
Математическая модель такого случайного опыта G называется вероятностным пространством и обозначается 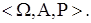 Сокращенно
Сокращенно 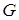 ~
~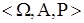 , где
, где
 - множество исходов опыта G;
- множество исходов опыта G;
 - множество случайных событий, наблюдаемых в опыте G (класс подмножеств
- множество случайных событий, наблюдаемых в опыте G (класс подмножеств  , называемый алгеброй или
, называемый алгеброй или -алгеброй);
-алгеброй);
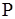 - вероятность случайных событий (вероятностная мера на измеримом пространстве
- вероятность случайных событий (вероятностная мера на измеримом пространстве  ). Связь вероятностной и теоретико-множественной терминологии отражена в таблице 1.
). Связь вероятностной и теоретико-множественной терминологии отражена в таблице 1.
2.1. Алгебра событий. Рассмотрим случайный опыт G, множество исходов которого  конечно. В такой модели событием назовем любое подмножество
конечно. В такой модели событием назовем любое подмножество  .
.
Пример. Случайный опыт G - выбор наудачу одной кости из полного набора костей домино. Возможные математические модели данного опыта:
Модель 1.
 .
.
 - совокупность всех подмножеств
- совокупность всех подмножеств  .
.
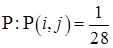 ,
,  (о вероятности см. ниже).
(о вероятности см. ниже).
Модель 2.
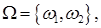 где
где  означает, что выбран дубль, а
означает, что выбран дубль, а  - не дубль.
- не дубль.
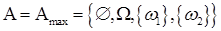 , где
, где  - невозможное событие;
- невозможное событие;  - достоверное событие.
- достоверное событие.

Рассмотрим несколько возможных результатов опыта G:
1) А- выбран дубль.
2) В - сумма очков на выбранной кости равна 6.
В первой модели А = {(0.0), (1,1), (2,2), (3,3). (4.4), (5,5), (6,6)};
В ={(0,6), (1.5), (2.4), (3,3)}.
Во второй модели А =  -элементарное событие. В - не является событием, так как при появлении любого из исходов
-элементарное событие. В - не является событием, так как при появлении любого из исходов  или
или  мы не можем сказать, осуществлялся или нет результат В.
мы не можем сказать, осуществлялся или нет результат В.
Вернемся к наиболее содержательной первой модели. Так как события в модели являются подмножествами, то к ним можно применять все теоретико-множественные операции. Например,
В А = {(0,6). (1,5), (2,4)},  ,
, 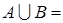 {(0,0), (1,1), (2,2), (3,3), (4.4), (5,5), (6,6), (0,6), (1.5), (2,4)},
{(0,0), (1,1), (2,2), (3,3), (4.4), (5,5), (6,6), (0,6), (1.5), (2,4)}, 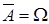 A - не дубль.
A - не дубль.
Задачи для самостоятельного решения
1. Мишень состоит из десяти кругов, ограниченных концентрическими окружностями с радиусами  . Событие
. Событие 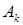 - попадание в круг радиуса
- попадание в круг радиуса  при одном выстреле по мишени. Описать множество исходов данного опыта. Что означают события
при одном выстреле по мишени. Описать множество исходов данного опыта. Что означают события  ,
, 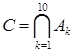 ,
, 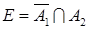 ,
,
 .
.
2. Электрическая цепь состоит из  элементов. Пусть событие А означает, что цепь безотказно работает в течение контрольного промежутка времени, а события
элементов. Пусть событие А означает, что цепь безотказно работает в течение контрольного промежутка времени, а события  - то же для
- то же для  -ого элемента;
-ого элемента; 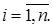
А. Выразить событие А и 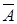 через события
через события 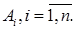 для цепей с параллельным и последовательным соединением элементов.
для цепей с параллельным и последовательным соединением элементов.
В. Выразить через  указанные ниже события: В - отказали все элементы, С - отказал хотя бы один элемент, D - безотказно работал один и только один из элементов, Е - отказали только два элемента..
указанные ниже события: В - отказали все элементы, С - отказал хотя бы один элемент, D - безотказно работал один и только один из элементов, Е - отказали только два элемента..
3. Случайный опыт – испытание трех приборов. События: А - хотя бы один из трех проверяемых приборов бракованный; В - все приборы доброкачественные. Что означают события a)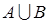 ; b)
; b)  c)
c)  d)
d) 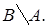 .
.
4. Опыт состоит в однократном бросании игральной кости. Описать возможные для данного опыта множества исходов. В каждой из предложенных моделей указать события: А - число очков, выпавших на верхней грани игральной кости, кратно трем; В - на верхней грани выпало нечетное число очков: С - число очков больше трех; D - число очков меньше семи; Е - число очков 0,5; F - число очков от 0,5 до 1,5. Установить пары совместных событий. Описать события 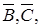


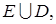

5. Пусть А и В - произвольные события, наблюдаемые в опыте G.
Проверить следующие равенства
a)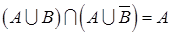 ;
;
b)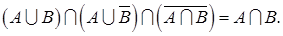
6. Пусть число исходов равно 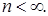 Указать минимальное и максимальное возможные значения для числа всех случайных событий.
Указать минимальное и максимальное возможные значения для числа всех случайных событий.
7. Может ли быть : a) число исходов конечно, а число всех случайных событий бесконечно; b) число всех случайных событий конечно, а число исходов бесконечно; c) число исходов больше, чем число всех событий.
В последующих пунктах мы рассмотрим примеры вероятностных пространств 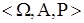 , объединенных интуитивным понятием равновозможности результатов опыта. .
, объединенных интуитивным понятием равновозможности результатов опыта. .
2.2. Классическая схема (модель). Рассмотрим опыт G, число возможных исходов которого конечно  и все исходы равновозможны, т.е. непредпочтительны друг перед другом или имеют одинаковые шансы к появлению. Тогда
и все исходы равновозможны, т.е. непредпочтительны друг перед другом или имеют одинаковые шансы к появлению. Тогда
 ,
, 
Обратимся к примеру п.2.1. В первой модели вероятность того, что выбранная наудачу кость окажется дублем 
т.е. в длинной серии испытаний (каждый раз выбираем случайным образом одну кость из тщательно перемешанного полного набора) примерно четверная часть из них закончится появлением дубля.
В этой же модели 
Во второй модели два возможных исхода опыта не являются равновоз-можными, т.е. в длинной серии независимых испытаний не дубль появляется чаще, чем дубль. В этой модели можно воспользоваться только статистическим способом задания вероятностей элементарных событий .
 Поучительным примером невозможности выбора и обоснования вероятностной модели на основании априорных не физических соображений является разнообразие вероятностных распределений для различных способов размещения физических частиц по ячейкам, например, электронов по орбитам. До настоящего времени известно три модели:
Поучительным примером невозможности выбора и обоснования вероятностной модели на основании априорных не физических соображений является разнообразие вероятностных распределений для различных способов размещения физических частиц по ячейкам, например, электронов по орбитам. До настоящего времени известно три модели:
Максвела-Больцмана - все  размещений
размещений  различных частиц по
различных частиц по  различным ячейкам равновероятны.
различным ячейкам равновероятны.
Бозе-Энштейна - все 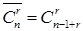 способов заполнения
способов заполнения  различных ячеек
различных ячеек  неразличимыми частицами равновероятны (в статистической механике показано, что это предположение справедливо для фотонов, атомных ядер и атомов, содержащих четное число элементарных частиц)
неразличимыми частицами равновероятны (в статистической механике показано, что это предположение справедливо для фотонов, атомных ядер и атомов, содержащих четное число элементарных частиц)
Ферми-Дирака - все  способов распределения равновероятны (эта модель применима к электронам, нейтронам и протонам).
способов распределения равновероятны (эта модель применима к электронам, нейтронам и протонам).
Задачи для самостоятельного решения
1. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера. Полученные кубики тщательно перемешаны. Определить вероятность того, что наудачу извлеченный кубик будет иметь: а) три окрашенные грани; b) только две окрашенные грани; с) только одну окрашенную грань; d) не имеет окрашенных граней.
2. Ребенок играет с 10 буквами разрезной азбуки А,А,А,Е,И,К,М,М,Т,Т. Какова вероятность того, что при случайном расположении букв в ряд он получит слово МАТЕМАТИКА ?
Для решения задачи рекомендуем построить две модели: в одной все десять карточек считать различными, в другой - карточки с одинаковыми буквами неразличимы. Получив, естественно, одно и то же значение вероятности, объясните это.
3. У человека N ключей, из которых только один подходит к его двери. Он последовательно испытывает их, выбирая случайным образом (без возвращения), найти вероятность того, что этот процесс закончится на k-ом испытании.
4. Абонент забыл две последние цифры номера телефона и потому набрал их наудачу, помня лишь то, что а) эти цифры различны; в) эти цифры нечетные. Найти вероятность того, что номер набран правильно.
5. В шахматном турнире участвуют 20 человек, которые по жребию распределяются на две группы по 10 человек. Найти вероятность того, что а) двое наиболее сильных игроков будут играть в разных группах; в) четверо наиболее сильных игроков попадут по два в разные группы.
6. Из урны, содержащей шары с номерами 1,2,.....9, пять раз наугад вынимают шар и каждый раз возвращают обратно. Найти вероятность того, что из номеров вынутых шаров можно составить возрастающую последовательность.
7. Десять студентов договорились о поездке за город, но не договорились о вагоне. Поэтому каждый из них выбирает для себя вагон случайным образом. Найти вероятность того, что а) все попадут в разные вагоны; в) все попадут в первый вагон; с) все попадут в один вагон, считая число вагонов  .
.
8. В отделение связи поступило шесть телеграмм. Телеграммы случайным образом распределяют по четырем каналам, причем каждая телеграмма может быть передана по любому из четырех каналов. Найти вероятность того, что на первый канал попадут три телеграммы, на второй - две телеграммы, на третий - одна телеграмма и четвертый канал не будет загружен.
2.3. Геометрическая схема. Геометрическое определение вероятности обобщает классическое на случай бесконечного множества исходов  , считая
, считая  некоторым подмножеством Rn , например, промежуток для п = 1; круг, прямоугольник для
некоторым подмножеством Rn , например, промежуток для п = 1; круг, прямоугольник для  = 2; шар, параллелепипед для
= 2; шар, параллелепипед для  = 3. Математическое описание опыта G - бросание случайным образом идеальной частицы (точки) в область
= 3. Математическое описание опыта G - бросание случайным образом идеальной частицы (точки) в область  или выбор наудачу точки из области
или выбор наудачу точки из области  - принято называть геометрической схемой. В этой модели
- принято называть геометрической схемой. В этой модели  - ограниченное множество Rn, имеющее n-мерный объем ( меру Лебега),
- ограниченное множество Rn, имеющее n-мерный объем ( меру Лебега),  и
и  ;
;  - класс измеримых подмножеств
- класс измеримых подмножеств  ;
; 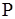 - вероятностная мера на
- вероятностная мера на  и вероятность попадания точки в область А считается равной
и вероятность попадания точки в область А считается равной
 .
.
Таким образом, вероятность попадания "случайно брошенной" точки в определенное подмножество  пропорциональна мере этого подмножества и не зависит от его расположения и формы.
пропорциональна мере этого подмножества и не зависит от его расположения и формы.
Пример. В круг единичного радиуса бросается случайным образом точка. Найти вероятность того, что эта точка попадает в круг радиуса 0,5: а) с тем же центром; в) с центром в точке С и ОС =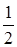 OD, где O - центр окружности, OD- радиус окружности.
OD, где O - центр окружности, OD- радиус окружности.
a) 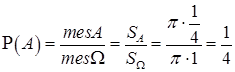 ; b)
; b) 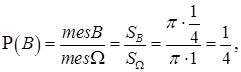
т.е. очевидно  , так как
, так как 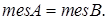
Задачи для самостоятельного решения.
1. Поступления каждого из двух сигналов в приемник равновозможны и независимы в любой момент промежутка времени Т. Определить вероятность того, что приемник будет "забит", что происходит в том случае, когда промежуток времени между моментами поступления обоих сигналов меньше 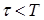 .
.
2. Два парохода должны в течение суток подойти к одному и тому же причалу. Определить вероятность того, что одному из пароходов придется ожидать освобождения причала, если время стоянки первого парохода один час, второго - два часа, и каждый из них независимо друг от друга появляется у причала в случайный момент времени в течение данных суток.
3. В круг вписан квадрат. Точка наудачу бросается в круг. Найти вероятность того, что она попадет в квадрат.
4. В квадрат с вершинами (0;0), (0;1), (1;0), (1;1) наудачу брошена точка М. Пусть  будут ее координаты. Найти вероятность того, что корни уравнения
будут ее координаты. Найти вероятность того, что корни уравнения 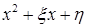 = 0 а) действительны; в) оба положительны.
= 0 а) действительны; в) оба положительны.
5. Какова вероятность того, что сумма двух независимым образом наугад взятых положительных чисел, каждое из которых не больше единицы, не превзойдет единицы, а их произведение будет не больше 2/9?
6. Пусть  и
и 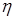 определены так же, как в задаче 4. Для
определены так же, как в задаче 4. Для  найти вероятность того, что: а)
найти вероятность того, что: а)  ; в)
; в)  ; c)
; c)  ;
;
d)  ; е)
; е)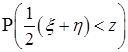 .
.
§ 3. Свойства вероятностей случайных событий. Условная вероятность. Стохастически независимые случайные события
Перечислим ряд свойств вероятностей случайных событий, которые являются фактически математическим отражением основных свойств частоты.
1. Вероятность достоверного события равна единице 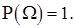
Заметим, что в общей модели случайного опыта это утверждение является аксиомой нормировки.
2. Вероятность невозможного события равна нулю 
3. Сумма вероятностей противоположных событий равна 1

4.Свойство монотонности вероятностной меры: 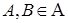 и
и 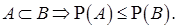
5. 
6. 
Условной вероятностью события 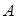 при условии, что событие В произошло, называется отношение вероятности совместного осуществления этих событий к вероятности того события, которое произошло
при условии, что событие В произошло, называется отношение вероятности совместного осуществления этих событий к вероятности того события, которое произошло
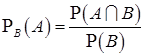 ,
, 
Можно показать, что вероятность одновременного осуществления п событий (п = 1,2,...)
 , если
, если 
События  стохастически независимы, если для любого подмножества
стохастически независимы, если для любого подмножества 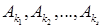
 имеет место равенство
имеет место равенство 
Таким образом, для выяснения стохастической независимости событий необходимо проверить выполнение  условий.
условий.
События  попарно независимы, если стохастически независимы любые два события этой совокупности, т.е. необходимо проверить выполнение
попарно независимы, если стохастически независимы любые два события этой совокупности, т.е. необходимо проверить выполнение 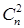 условий. Это означает, что попарная независимость является более слабым условием.
условий. Это означает, что попарная независимость является более слабым условием.
Пример. Понимая под надежностью некоторой электрической схемы вероятность безотказной работы этой схемы в течение контрольного промежутка времени и, учитывая свойства вероятностей случайных событий, решим следующую задачу.
Найти надежность  электрической схемы, состоящей из
электрической схемы, состоящей из  идентичных элементов, которые выходят из строя независимо друг от друга, и надежность каждого равна
идентичных элементов, которые выходят из строя независимо друг от друга, и надежность каждого равна 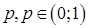 в случае
в случае
а) последовательного соединения этих элементов;
b) параллельного соединения.
a) 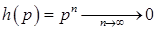 , т.е. нанизывая последовательно даже очень хорошие элементы, мы можем загубить этот участок цепи.
, т.е. нанизывая последовательно даже очень хорошие элементы, мы можем загубить этот участок цепи.
b)  , т.е. мы можем повысить надежность данного участка цепи, имея достаточно большое количество элементов, возможно и не очень хороших.
, т.е. мы можем повысить надежность данного участка цепи, имея достаточно большое количество элементов, возможно и не очень хороших.
Задачи для самостоятельного решения
1. Стрелок производит один выстрел в мишень, состоящую из центрального круга и двух концентрических колец. Вероятности попадания в круг и кольца соответственно равны 0,20; 0,15 и 0,10. Определить вероятность непопадания в мишень.
2. Вероятность выхода из строя k-го блока вычислительной машины за время T равна  , k = 1,2,... ,
, k = 1,2,... , . Определить вероятность выхода из строя за указанный промежуток времени хотя бы одного из
. Определить вероятность выхода из строя за указанный промежуток времени хотя бы одного из  блоков этой машины, если работа всех блоков взаимно независима.
блоков этой машины, если работа всех блоков взаимно независима.
3. В партии, состоящей из N изделий, имеется М дефектных. Из партии выбираются случайным образом  изделий. Если среди контрольных деталей окажется более т дефектных, бракуется вся партия. Найти вероятность того, что партия будет забракована.
изделий. Если среди контрольных деталей окажется более т дефектных, бракуется вся партия. Найти вероятность того, что партия будет забракована.
4. Разрыв электрической цепи может произойти вследствие выхода из строя элемента К или двух элементов  и
и 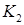 , надежности которых соответственно равны 0,7; 0,8 и 0,9. Определить вероятность разрыва электрической цепи, считая, что элементы выходят из строя независимо друг от друга.
, надежности которых соответственно равны 0,7; 0,8 и 0,9. Определить вероятность разрыва электрической цепи, считая, что элементы выходят из строя независимо друг от друга.
 |
5. Найти надежность электрической схемы, состоящей из нескольких идентичных элементов, которые выходят из строя независимо друг от друга с вероятностью
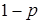 ,
, 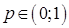 :
:
6. Предлагается два способа дублирования последовательно соединенных пяти элементов: дублируется вся схема или дублируется каждый элемент. Сравнить эффективности (надежности) этих способов дублирования. Заметим, что дублирование некоторой схемы (элемента) означает параллельное подключение аналогичной схемы (элемента), которая работает независимо от исходной.
7. События  стохастически независимы и равновероятны. Найти вероятность: а) появления хотя бы одного из этих событий; b) не появления всех этих событий; с) появления только одного из них; d) появления только
стохастически независимы и равновероятны. Найти вероятность: а) появления хотя бы одного из этих событий; b) не появления всех этих событий; с) появления только одного из них; d) появления только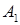 .
.
8. Выбирают наудачу один член разложения определителя п-го порядка. Какова  вероятность того, что он не содержит элементов главной диагонали? Найти
вероятность того, что он не содержит элементов главной диагонали? Найти  предел вероятности
предел вероятности  при
при  .
.
9. Абонент забыл последнюю цифру номера телефона и поэтому набирает ее наудачу. Определить вероятность того, что ему придется звонить не более, чем в 3 места. Как изменится вероятность, если известно, что последняя цифра нечетная?
10. Брошены независимым образом две игральные кости. Положим  - число очков, выпавшее на первой кости, делится на
- число очков, выпавшее на первой кости, делится на 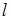 ,
,  - на второй кости делится на
- на второй кости делится на 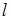 ,
, 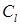 - сумма очков, выпавших на первой и второй костях, делится на
- сумма очков, выпавших на первой и второй костях, делится на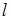 . Установить, являются ли стохастически независимыми события а)
. Установить, являются ли стохастически независимыми события а) и
и  ; b )
; b ) и
и  для различных
для различных 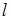 и
и 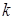 ; с)
; с) и
и 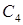 ; d)
; d) 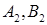 и
и  .
.
11. Вероятность того, что письмо в столе, равна р, причем с равной вероятностью письмо может находиться в любом из 8 ящиков стола. Было просмотрено 7 ящиков, но письмо не нашли. Какова вероятность того, что письмо в восьмом ящике?
12. Бросают три кости. Какова вероятность того, что хотя бы на одной из них выпадает одно очко, если на всех трех костях выпали разные грани?
13.Известно, что при бросании 10 костей появилась по крайней мере одна единица. Какова вероятность того, что появились две или более единицы?
§ 4. Формула полной вероятности. Формула Байеса
Пусть события  образуют разбиение множества исходов
образуют разбиение множества исходов  : 1.
: 1.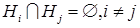 ;
;
2.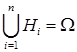 ,
,
т.е. в результате опыта одно и только одно из этих событий обязательно происходит. Тогда вероятность события А вычисляется по формуле полной вероятности
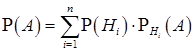 .
.
События  часто называют гипотезами, а вероятности
часто называют гипотезами, а вероятности 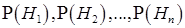 - априорными вероятностями гипотез. Формула Байеса
- априорными вероятностями гипотез. Формула Байеса
 , где
, где 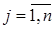
дает возможность произвести пересчет вероятностей гипотез  . Условные вероятности
. Условные вероятности 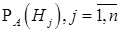 принято называть апостериорными вероятностями гипотез.
принято называть апостериорными вероятностями гипотез.
Условно задачи, решаемые по формулам, можно разбить на два типа. Задачи первого типа имеют дело с экспериментами, которые состоят из двух этапов и оба этапа случайны. Тогда в качестве событий, образующих разбиение  , берут события, которые полностью описывают первый этап эксперимента.
, берут события, которые полностью описывают первый этап эксперимента.
Задача 1. Имеются три одинаковые с виду партии деталей. В первой, изготовленной заводом № 1, 5% брака, во второй, изготовленной заводом № 2, 3% брака, а в третьей (завод № 3) - 10% брака. Наугад выбирается одна из партий, а затем из этой партии наудачу выбирается одна деталь. Определить вероятность того, что она бракованная.
Решение. Первый этап опыта - выбор наудачу одной из трех партий деталей, второй - выбор наудачу детали из выбранной партии. Очевидно, что
события 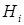 - выбрана партия деталей, изготовленная заводом
- выбрана партия деталей, изготовленная заводом  ,
,  = 1, 2,3, образуют разбиение
= 1, 2,3, образуют разбиение  и вероятности
и вероятности 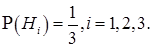 Тогда вероятность выбрать бракованную деталь (событие А) по формуле полной вероятности будет равна
Тогда вероятность выбрать бракованную деталь (событие А) по формуле полной вероятности будет равна 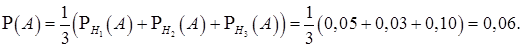
Задача 2. Вероятность для изделий некоторого производства удовлетворять стандарту равна 0,96. Предлагается упрощенная система испытаний, дающая положительный результат с вероятностью 0,98 для изделий, удовлетворяющих стандарту; а для изделий, которые не удовлетворяют стандарту, с вероятностью 0,05. Какова вероятность того, что изделие, выдержавшее испытание, удовлетворяет стандарту? Интересующая нас вероятность 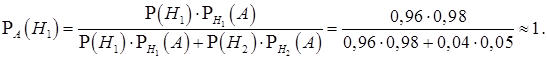
Отсюда вывод: в том случае, когда упрощенная система испытаний дает положительный результат, деталь с вероятностью, близкой к единице, является стандартной. Другими словами, данная система контроля является хорошим "фильтром "для бракованных изделий.
В задачах второго типа появляются эксперименты, условия проведения которых точно не известны, но о них (условиях) можно сделать  исключа- ющих друг друга предположений (гипотез).
исключа- ющих друг друга предположений (гипотез).
Задача 3. Из сосуда, содержащего п шаров, берут наудачу один. Определить вероятность того, что он белый, если все предположения о первоначальном числе белых шаров равновозможны.
Решение. В задаче неизвестными для нас будут условия проведения выбора (число белых шаров в сосуде), относительно которых мы можем выдвинуть (п + 1) гипотезу  , где
, где 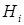 означает i белых шаров в сосуде, i= 0,1,... , п. Так как по условию задачи гипотезы равновероятны, то, обозначив
означает i белых шаров в сосуде, i= 0,1,... , п. Так как по условию задачи гипотезы равновероятны, то, обозначив 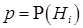 , получим
, получим
 ,
,
откуда 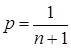 . Тогда по формуле полной вероятности, вероятность со-
. Тогда по формуле полной вероятности, вероятность со-
бытия (выбран белый шар из сосуда) равна

Задача 4. Из сосуда, содержащего п шаров, взяли наудачу один шар и он оказался белым. Какое предположение о количестве белых шаров наиболее вероятно, если до опыта все предположения о числе белых шаров были равновозможны?
Решение. Так же, как в задаче 3, априорные вероятности гипотез одинаковы и равны  , i = 0,1,... ,n. Известно, что опыт произвели и произошло событие А (выбранный наудачу шар оказался белым). Очевидно, что появление события изменяет шансы осуществления каждой из гипотез. Так, например, если до опыта гипотеза
, i = 0,1,... ,n. Известно, что опыт произвели и произошло событие А (выбранный наудачу шар оказался белым). Очевидно, что появление события изменяет шансы осуществления каждой из гипотез. Так, например, если до опыта гипотеза 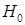 имела положительную вероятность, то после опыта она имеет нулевые шансы к осуществлению, то есть
имела положительную вероятность, то после опыта она имеет нулевые шансы к осуществлению, то есть 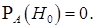
Для ответа на вопрос задачи вспомним, что


Тогда 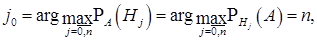 то есть наиболее вероятной будет гипотеза
то есть наиболее вероятной будет гипотеза  - все шары белые, что интуитивно также ясно.
- все шары белые, что интуитивно также ясно.
Задачи для самостоятельного решения
1. Пересчитать вероятности гипотез в задаче 4 стр.14 при  =5.
=5.
2. Из полного набора костей домино наугад одна за другой берутся две кости. Определить вероятность того, что вторую кость можно приставить к первой.
3. Из сосуда, содержащего 5 белых и 4 черных шара, был потерян один шар. После этого из сосуда наудачу выбран шар. Найти вероятность того, что выбранный шар окажется белым.
4. В ящике находятся 15 теннисных мячей, из которых 9 новых. Для первой игры наугад берутся три мяча, которые после игры возвращаются в ящик. Затем для второй игры наугад выбираются три мяча. Найти вероятность того, что все мячи, взятые для второй игры, новые.
5. В сосуд, содержащий п шаров, опущен белый шар. Какова вероятность извлечь из этого сосуда белый шар, если все предположения о первоначальном числе белых шаров в сосуде равновозможны?
6. Имеется 10 карточек, на которых написаны числа 3,3,3,4,4,5,5,6,6,6. Две из этих карточек выбираются наугад одна за другой. Число, написанное на первой карточке, берется за числитель, на второй - за знаменатель дроби. Найти вероятность того, что дробь будет правильной.
7. Группа студентов, сдающих экзамен, состоит из 4 отличников, 10 хорошистов и 20 слабых студентов. Отличник всегда сдает экзамен на "5". Хорошист может получить "4" или "5" с равными вероятностями. Слабый студент может получить "4", "3" или "2" с равными вероятностями. Наудачу выбранный студент получил "4". Что вероятнее - это был хорошист или слабый студент?
8. Имеется n урн, в каждой из которых находится а белых и b черных шаров. Наудачу выбранный шар из первой урны перекладывается во вторую, затем из второй - в третью и т.д. После такого перекладывания из последней урны наудачу выбирается один шар. Найти вероятность того, что будет выбран белый шар.
9. По каналу связи может быть передана одна из трех последовательностей букв: АААА, ВВВВ, СССС, причем априорные вероятности каждой из последовательностей есть соответственно 0,3; 0,4; 0,3. Известно, что действие шумов уменьшает вероятность правильного приема каждой буквы до 0,6, а вероятность приема переданной буквы за любую другую становится равной 0,2 и 0,2. Предполагается, что буквы искажаются независимо друг от друга. Найти вероятность того, что была передана последовательность АААА, если на приемном устройстве было получено - АВСА.
10. Из 18 стрелков пятеро попадают в мишень с вероятностью 0,8; семеро - с вероятностью 0,7; четверо - с вероятностью 0,6 и двое - с вероятностью 0,5. Наудачу выбранный стрелок произвел выстрел, но в мишень не попал. К какой из групп вероятнее всего принадлежал этот стрелок?
11. В техникуме  студентов, из которых
студентов, из которых 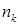 (k = 1,2,3) человек учатся k-й год. Среди двух наудачу выбранных студентов оказалось, что один из них учится больше второго. Какова вероятность того, что этот студент учится третий год?
(k = 1,2,3) человек учатся k-й год. Среди двух наудачу выбранных студентов оказалось, что один из них учится больше второго. Какова вероятность того, что этот студент учится третий год?
§ 5. Схема Бернулли.
Испытания Бернулли - это  независимых повторений некоторого опыта, в результате которого может произойти или не произойти некоторое событие, условно называемое "успехом", с одной и той же вероятностью р для каждого из повторений.
независимых повторений некоторого опыта, в результате которого может произойти или не произойти некоторое событие, условно называемое "успехом", с одной и той же вероятностью р для каждого из повторений.
В принятой нами аксиоматике испытание – это некоторое вероятностное пространство. Тогда схема Бернулли строится следующим образом:
 где
где 
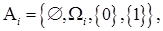



 Тогда
Тогда
 где
где 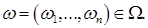
Вероятность того, что ровно k опытов из  закончатся "успехом " будет
закончатся "успехом " будет


Пример. Что вероятнее: выиграть у равносильного противника (ничейный исход партии исключен) три партии из четырех или пять из восьми?
Решение. Так как противники равносильны, то вероятность выигрыша и проигрыша каждой партии одинаковы и равны 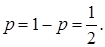 Тогда вероятность выиграть три партии из четырех
Тогда вероятность выиграть три партии из четырех 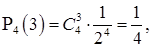
а вероятность выиграть пять партий из восьми 
Так как  , то вероятнее выиграть три партии из четырех.
, то вероятнее выиграть три партии из четырех.
Задачи для самостоятельного решения.
1. Определить вероятность того, что в результате 10 независимых бросаний честной монеты герб появится: a) три раза; b) не более трех раз.
2. При раздаче колоды в 52 карты четырем игрокам один из них три раза подряд не получал тузов. Есть ли у него основание жаловаться на "невезение"?
3. Два баскетболиста делают по три броска мячом в корзину независимо друг от друга. Вероятности попадания мяча при каждом броске равны соответственно 0,6 и 0,7. Найти вероятность того, что: а) у обоих будет равное число попаданий; б) у первого баскетболиста будет больше попаданий, чем у второго.
4. Произведено 20 независимых испытаний, каждое из которых заключается в одновременном бросании трех монет. Найти вероятность того, что хотя бы в одном испытании появятся три герба.
5. При передаче сообщения вероятность искажения одного знака равна 0,1. Какова вероятность того, что сообщение из 10 знаков: a) не будет искажено; b) содержит ровно три искажения; c) содержит не более трех искажений? Предполагается, что знаки передаются независимо друг от друга.
6. Событие B наступает в том случае, если событие A появится не менее трех раз. Определить вероятность появления события B, если вероятность появления события А при одном опыте равна 0,3 и произведено: a) 5 независимых опытов; b) 7 независимых опытов.
§ 6. Случайные величины
Пусть G - случайный опыт, математическое описание которого<  >. Часто при решении практических задач нас интересуют не сами исходы
>. Часто при решении практических задач нас интересуют не сами исходы  , а их числовые характеристики, т.е. величины, значения которых зависят от исходов опыта. Такую величину естественно назвать случайной.
, а их числовые характеристики, т.е. величины, значения которых зависят от исходов опыта. Такую величину естественно назвать случайной.
Определение. Числовая функция, определенная на множестве исходов  таким образом, что
таким образом, что  для любого
для любого 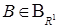 называется случайной величиной (с.в.).
называется случайной величиной (с.в.). Последнее условие
Последнее условие  измеримости позволяет построить выборочное пространство с.в. в виде тройки
измеримости позволяет построить выборочное пространство с.в. в виде тройки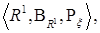 где мера
где мера  определяется равенством
определяется равенством  , называется распределением вероятностей с.в.
, называется распределением вероятностей с.в.  и представляет образ меры
и представляет образ меры 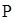 на
на 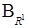 .
.
Мера  однозначно определяется функцией распределения (ф.р.) с.в.
однозначно определяется функцией распределения (ф.р.) с.в. 
 , коротко
, коротко 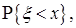
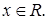
Ф.р. любой с.в. обладает тремя характеристическими свойствами:
1) неубывающая;
2) непрерывна слева;
3)
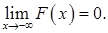 С помощью этой функции можно вычислить вероятность попадания значений с.в. в любой промежуток, так как
С помощью этой функции можно вычислить вероятность попадания значений с.в. в любой промежуток, так как 
 Тогда, например,
Тогда, например, 
По виду ф.р. (распределения вероятностей) можно осуществить классификацию с.в.: дискретные с.в.- ф.р. является кусочно-постоянной и представима в виде суммы


где  - возможные значения с.в.. a.
- возможные значения с.в.. a.  - соответствующие вероятности. Таблица
- соответствующие вероятности. Таблица
 , где : l)
, где : l) 
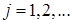 2)
2) 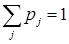
называется рядом распределения вероятностей с.в.  .
.
Абсолютно-непрерывные с.в.- ф.р. представима в виде
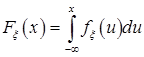 ,
, 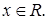
Функция  называется плотностью распределения вероятностей и обладает следующими характеристическими свойствами: 1)
называется плотностью распределения вероятностей и обладает следующими характеристическими свойствами: 1) 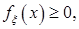
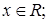
2) 
Сингулярные с.в. - 1. 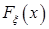 - непрерывна на
- непрерывна на 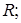 2.
2.  п.в. на
п.в. на 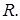
Определение. Начальным моментом порядка k с.в.  называется число
называется число 
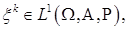 где
где  - совокупность всех абсолютно интегрируемых относительно меры
- совокупность всех абсолютно интегрируемых относительно меры 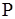 с.в. на
с.в. на  В частности
В частности  где
где  - дискретная с.в. , если ряд абсолютно сходится и
- дискретная с.в. , если ряд абсолютно сходится и 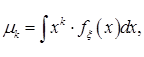 где
где  - абсолютно-непрерывная с.в., если интеграл абсолютно сходится,
- абсолютно-непрерывная с.в., если интеграл абсолютно сходится, 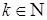 . Начальный момент 1-го порядка принято называть математическим ожиданием с.в.
. Начальный момент 1-го порядка принято называть математическим ожиданием с.в.  ( средним значением).
( средним значением).
Центральным моментом порядка k с.в.  называется число
называется число 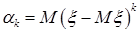 , если указанное математическое ожидание существует,
, если указанное математическое ожидание существует, 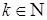 .. Очевидно, что
.. Очевидно, что 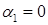 (среднее отклонение от среднего равно нулю);
(среднее отклонение от среднего равно нулю);  называется дисперсией с.в.
называется дисперсией с.в.  ( характеристика разброса возможных значений с.в. относительно среднего, что подтверждает неравенство Чебышева
( характеристика разброса возможных значений с.в. относительно среднего, что подтверждает неравенство Чебышева
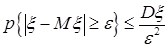 , где
, где 
 ).
).
Задача 1. Абсолютно-непрерывная с.в. имеет п.р.в.

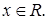
Найти : а) коэффициент 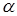 ; b) ф.р.; с)
; b) ф.р.; с)  ; d)
; d) 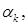
 Используя характеристические свойства п.р.в., получаем
Используя характеристические свойства п.р.в., получаем

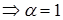 ;
;
b) 
Графики п.р.в. и ф.р.

с) 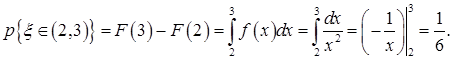
d) 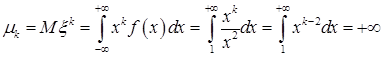 - расходится для
- расходится для 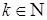 , значит, начальные, а следовательно, и центральные моменты не определены.
, значит, начальные, а следовательно, и центральные моменты не определены.
Задача 2. При передаче сообщения вероятность искажения одного знака равна 0,1. Построить ряд распределения числа искаженных знаков в сообщении, состоящем из 4-х независимо передаваемых знаков. Найти среднее и дисперсию числа искажений при передаче одного сообщения.
Ряд распределения вероятностей с.в.  , означающей число искаженных знаков из 4-х, имеет вид
, означающей число искаженных знаков из 4-х, имеет вид
| x | |||||
| Р | 0,6561 | 0,2916 | 0,0486 | 0,0036 | 0,0001 |
Заметим, что  имеет
имеет  распределение;
распределение; 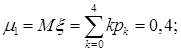
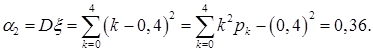
Задачи для самостоятельного решения
1. Задана таблица

| -1 | ||||

| -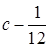
| 
| 
| 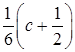
| 
|
При каком значении с эта таблица будет задавать ряд распределения некоторой случайной величины  ? Найти функцию распределения этой случайной величины, ее математическое ожидание и дисперсию.
? Найти функцию распределения этой случайной величины, ее математическое ожидание и дисперсию.
2. Ряд распределения вероятностей случайной величины  определяется формулами
определяется формулами 
Найти: 1) постоянную с ; 2) 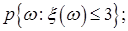 3) функцию распределения;
3) функцию распределения;
4) начальные и центральные моменты.
3. Производится  независимых опытов, в каждом из которых с вероятностью р появляется событие А. Построить ряд распределения 1) числа появлений противоположного события; 2) частоты появления события А в п опытах. Для этих случайных величин найти математическое ожидание и дисперсию.
независимых опытов, в каждом из которых с вероятностью р появляется событие А. Построить ряд распределения 1) числа появлений противоположного события; 2) частоты появления события А в п опытах. Для этих случайных величин найти математическое ожидание и дисперсию.
4. На пути движения автомашины четыре светофора. Каждый из них независимо от работы других светофоров с вероятностью 0,5 либо разрешает, либо запрещает автомашине дальнейшее движение. Построить ряд распределения числа светофоров, пройденных автомашиной подряд без остановки. Для этой случайной величины найти функцию распределения, математическое ожидание и дисперсию.
5. Производятся независимые выстрелы по мишени до первого промаха или пока не кончатся патроны. Построить ряд распределения для: 1) числа проведенных выстрелов; 2) числа попаданий, если имеется 5 патронов и вероятность попадания при одном выстреле 0,8; 3) числа промахов. Найти для построенных случайных величин функцию распределения, математическое ожидание и дисперсию.
6. Найти математическое ожидание и дисперсию случайных величин, имеющих типовые распределения: 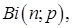
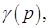

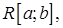


7. Из сосуда, содержащего т белых и п черных шаров, извлекаются шары до тех пор, пока не появится белый шар. Построить ряд распределения, функцию распределения и найти числовые характеристики для случайной величины  - число вынутых черных шаров, если a) выбор с возвращением; b) выбор без возвращения.
- число вынутых черных шаров, если a) выбор с возвращением; b) выбор без возвращения.
8. Проверяется  лампочек, каждая из которых с вероятностью р может иметь дефект. Лампочка ввинчивается в патрон и включается ток. При включении тока дефектная лампочка сразу же перегорает и заменяется другой. Построить ряд распределения числа лампочек, которое будет испробовано. Вычислить математическое ожидание и дисперсию при п = 6, р == 0,2.
лампочек, каждая из которых с вероятностью р может иметь дефект. Лампочка ввинчивается в патрон и включается ток. При включении тока дефектная лампочка сразу же перегорает и заменяется другой. Построить ряд распределения числа лампочек, которое будет испробовано. Вычислить математическое ожидание и дисперсию при п = 6, р == 0,2.
9. Из 20 приборов имеется 6 не точных. Найти функцию распределения, математическое ожидание и дисперсию числа точных приборов среди отобранных наудачу 5 приборов.
10. При каком значении с функция  ,
, 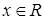 может быть плотностью распределения вероятностей некоторой случайной величины
может быть плотностью распределения вероятностей некоторой случайной величины  ?
?
1) 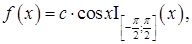
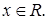
2) 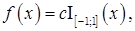
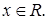
3) 
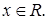
4) 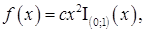
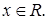
Найти функцию распределения этой случайной величины  . Вычислить вероятность того, что случайная величина
. Вычислить вероятность того, что случайная величина  примет значения из интервала
примет значения из интервала
(-1;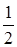 ); (0;1).
); (0;1).
11. Случайная величина  имеет распределение Рэлея с плотностью распределения вероятностей
имеет распределение Рэлея с плотностью распределения вероятностей
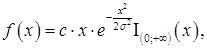
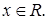
Найти коэффициент с, считая  заданным. Найти функцию распределения и числовые характеристики случайной величины
заданным. Найти функцию распределения и числовые характеристики случайной величины .
.
12. Случайная величина  имеет
имеет  распределение.
распределение.
1) Найти  при
при 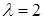 ; 2) Найти плотность распределения и числовые характеристики случайных величин a)
; 2) Найти плотность распределения и числовые характеристики случайных величин a)  b)
b)  c)
c)  .
.
13. Пусть  ~
~  распределение.
распределение.
1) Что больше  или
или  ?
?
2) Найти ф.р. и п.р.в. случайной величины  где
где 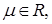
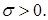
14. Найти абсциссы точек перегиба графика функции  если
если  имеет
имеет 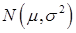 распределение. Найти
распределение. Найти  и
и 
15. Пусть  имеет
имеет 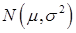 распределение. Найти п.р.в. и числовые характеристики с.в. a)
распределение. Найти п.р.в. и числовые характеристики с.в. a)  , если
, если 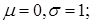 b)
b) 
16. Функция распределения случайной величины  имеет закон распределения арксинуса
имеет закон распределения арксинуса
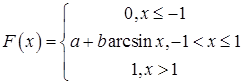 .
.
Определить постоянные а и  . Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины
. Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины . Найти
. Найти 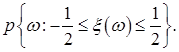
17. Модуль вектора скорости молекулы газа есть случайная величина, распределенная по закону Максвелла с плотностью распределения вероятностей

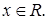
Найти среднюю скорость и дисперсию величины скорости молекулы.
18. Найти математическое ожидание, дисперсию и функцию распределения случайной величины 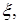 имеющей плотность распределения вероятностей
имеющей плотность распределения вероятностей
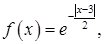
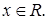
§ 7. Случайные векторы
Задачи для самостоятельного решения
1. Производится один выстрел по мишени. Вероятность попадания в мишень равна  . Рассмотрим случайный вектор
. Рассмотрим случайный вектор 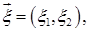 где
где  - число попаданий в мишень при этом выстреле, а
- число попаданий в мишень при этом выстреле, а  - число промахов. Построить ряд распределения. Найти функцию распределения этого случайного вектора и маргинальные функции распределения. Проверить стохастическую независимость координат этого вектора. Найти числовые характеристики.
- число промахов. Построить ряд распределения. Найти функцию распределения этого случайного вектора и маргинальные функции распределения. Проверить стохастическую независимость координат этого вектора. Найти числовые характеристики.
2. Случайный опыт 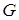 - два независимых выстрела по мишени; вероятность попадания при каждом из выстрелов равна
- два независимых выстрела по мишени; вероятность попадания при каждом из выстрелов равна . Рассмотрим случайный вектор
. Рассмотрим случайный вектор  , где
, где 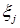 - число попаданий при j-ом выстреле
- число попаданий при j-ом выстреле  Найти функцию распределения случайного вектора и маргинальные распределения. Проверить стохастическую независимость координат и найти числовые характеристики.
Найти функцию распределения случайного вектора и маргинальные распределения. Проверить стохастическую независимость координат и найти числовые характеристики.
3. Случайный опыт G – два независимых бросания правильной игральной кости. Рассмотрим случайный вектор  , где 1)
, где 1) 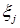 - число очков при j-ом бросании, j=1,2; 2)
- число очков при j-ом бросании, j=1,2; 2)  -минимальное число очков при двух бросаниях, а
-минимальное число очков при двух бросаниях, а  - максимальное. Построить ряд распределения случайного вектора
- максимальное. Построить ряд распределения случайного вектора  . Проверить стохастическую независимость, найти маргинальные распределения и числовые характеристики.
. Проверить стохастическую независимость, найти маргинальные распределения и числовые характеристики.
4.Случайный вектор  - дискретного типа. Найти распределение суммы
- дискретного типа. Найти распределение суммы 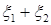 и произведения
и произведения 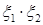 , если
, если
а)

| |||
| -1 | 0,1 | 0,2 | 0,1 |
| 0,3 | 0,1 | 0,2 |
b)
 x1 x1

| ||
| -1 | 0,125 | 0,375 |
| 0,375 | 0,125 |
c)
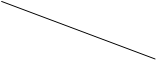 

| -1 | |
| 0,03 | 0,07 | |
| 0,15 | 0,35 | |
| 0,12 | 0,28 |
Найти также числовые характеристики и маргинальные распределения.
5.Случайный вектор  имеет независимые компоненты и
имеет независимые компоненты и 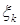 ~
~  , k=1,2. Найти a) распределение вероятностей с.в.
, k=1,2. Найти a) распределение вероятностей с.в.  ;
;
b)  ; c) найти распределение вероятностей с.в.
; c) найти распределение вероятностей с.в. 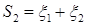 , предполагая, что
, предполагая, что 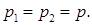
6. Пусть случайный вектор 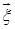 имеет независимые компоненты и
имеет независимые компоненты и 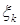 ~
~  ,
,  . Доказать, что с.в.
. Доказать, что с.в. 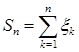 ~
~ . Найти
. Найти 
 ,
, 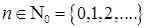 .
.
7. Случайный вектор  имеет плотность распределения вероятностей 1)
имеет плотность распределения вероятностей 1)  ,
, 
2) 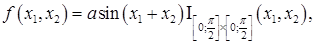
 Найти коэффициент
Найти коэффициент 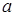 , функцию распределения случайного вектора, найти маргинальные распределения и числовые характеристики. Проверить стохастическую независимость компонент данного вектора.
, функцию распределения случайного вектора, найти маргинальные распределения и числовые характеристики. Проверить стохастическую независимость компонент данного вектора.
8. Случайный вектор  . Найти плотность распределения вероятности случайного вектора
. Найти плотность распределения вероятности случайного вектора 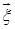 и маргинальные плотности, если : 1)
и маргинальные плотности, если : 1)  - квадрат с координатами вершин (-1;-1) , (-1; 1) , (1;-1) , (1;1); 2)
- квадрат с координатами вершин (-1;-1) , (-1; 1) , (1;-1) , (1;1); 2)  - квадрат с координатами вершин (-1;0) , (0;1) , (1;0) , (0;-1); 3)
- квадрат с координатами вершин (-1;0) , (0;1) , (1;0) , (0;-1); 3)  - круг с центром в начале координат и радиусом равным 1.
- круг с центром в начале координат и радиусом равным 1.
9. Пусть случайный вектор 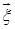 имеет независимые компоненты и a)
имеет независимые компоненты и a) 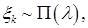
 ; b)
; b) 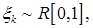
 . Найти функцию распределения и плотность распределения вероятностей с.в.
. Найти функцию распределения и плотность распределения вероятностей с.в. 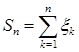 . В случае распределения b) найти и построить график плотности распределения вероятностей
. В случае распределения b) найти и построить график плотности распределения вероятностей  для
для 
10. Пусть 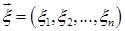 случайный вектор с независимыми компонентами имеет абсолютно непрерывное распределение вероятностей. Найти плотность распределения вероятностей с.в. a)
случайный вектор с независимыми компонентами имеет абсолютно непрерывное распределение вероятностей. Найти плотность распределения вероятностей с.в. a)  ; b)
; b) ; c)
; c) 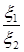 ; d)
; d) 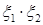 . Найти тип распределения, если
. Найти тип распределения, если  и
и  . Найти числовые характеристики полученных с.в..
. Найти числовые характеристики полученных с.в..
11. Найти распределение суммы 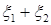 , если
, если  и
и  независимые с.в. и a)
независимые с.в. и a)  ; b)
; b) 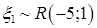 ;
; 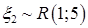 ; c)
; c)

12. Может ли заданная функция быть плотностью распределения вероятностей многомерного нормального распределения? Если да, то найти соответствующие параметры  и
и  . Найти также маргинальные распределения.
. Найти также маргинальные распределения.
1) 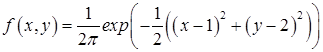 ;
;
2)  ;
;
3) 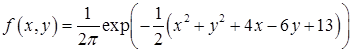 .
.
13. Записать плотность распределения вероятностей случайного вектора 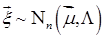 и найти функцию распределения, если
и найти функцию распределения, если  -диагональная матрица.
-диагональная матрица.
14. Дана плотность распределения вероятностей случайного вектора  :
:  . Найти маргинальные распределения. Проверить стохастическую независимость компонент этого случайного вектора.
. Найти маргинальные распределения. Проверить стохастическую независимость компонент этого случайного вектора.
15. Доказать, что если компоненты случайного вектора  независимы, причем
независимы, причем 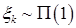 для
для 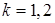 , то независимы с.в
, то независимы с.в  и
и 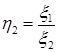 .
.
16. Найти распределение вероятностей и числовые характеристики с.в. , если случайный вектор
, если случайный вектор 
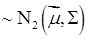 , где
, где
a) 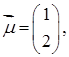
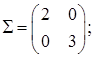 b)
b) 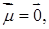

17. Пусть случайный вектор  имеет независимые компоненты, причем
имеет независимые компоненты, причем 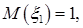


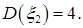 Найти: a)
Найти: a) 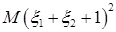 ; b)
; b) 
§8. Характеристическая функция случайной величины и случайного
Вектора
, Она представляет преобразование Фурье меры и в двух частных случаях имеет вид: А. , где - дискретная с.в. . B. , , где - абсолютно-непрерывная с.в..– Конец работы –
Используемые теги: Теория, вероятностей0.057
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов