рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вектора
Реферат Курсовая Конспект
Вектора
Вектора - раздел Математика, ТЕОРИЯ ВЕРОЯТНОСТЕЙ Рассмотрим С.в. ...
Рассмотрим с.в. 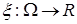 , наблюдаемую в опыте
, наблюдаемую в опыте 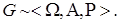 Ее распределение вероятностей однозначно определяется характеристической функцией (х.ф.)
Ее распределение вероятностей однозначно определяется характеристической функцией (х.ф.) 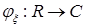 , задаваемой равенством
, задаваемой равенством
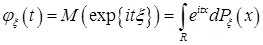 ,
, 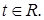 Она представляет преобразование Фурье меры
Она представляет преобразование Фурье меры  и в двух частных случаях имеет вид:
и в двух частных случаях имеет вид:
А. 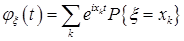 ,
, 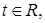 где
где  - дискретная с.в. .
- дискретная с.в. .
B.  ,
,  , где
, где  - абсолютно-непрерывная с.в..
- абсолютно-непрерывная с.в..
Характеристическая функция с.в.  обладает свойствами:
обладает свойствами:
1. 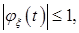

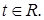
2. 
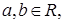
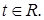
3.  если
если  стохастически независимы и
стохастически независимы и 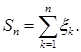
4. 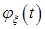 - непрерывна на всей числовой оси.
- непрерывна на всей числовой оси.
5.  при
при  если
если 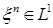 и
и  .
.
Пример. Если  то
то 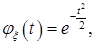
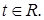
Для случайного вектора 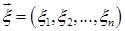 можно ввести понятие характеристической функции по аналогии со скалярным случаем
можно ввести понятие характеристической функции по аналогии со скалярным случаем


Эта функция обладает свойствами аналогичными свойствам 1-5 скалярной характеристической функции.
Задачи для самостоятельного решения
1. Найти х.ф. типовых распределений и вычислить все начальные моменты.
2. С помощью свойств х.ф. найти законы распределения с.в. 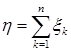 , где с.в.
, где с.в.  стохастически независимы, одинаково распределены и имеют a) нормальный закон распределения; b) закон распределения Коши; c) биномиальный закон распределения; d) закон распределения Пуассона.
стохастически независимы, одинаково распределены и имеют a) нормальный закон распределения; b) закон распределения Коши; c) биномиальный закон распределения; d) закон распределения Пуассона.
3. Доказать, что с.в.  имеет симметричное относительно нуля распределение
имеет симметричное относительно нуля распределение 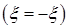 тогда и только тогда, когда х.ф.
тогда и только тогда, когда х.ф. 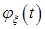 вещественнозначна.
вещественнозначна.
4. Могут ли следующие функции быть х.ф. некоторых с.в.: 1) 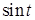 ; 2)
; 2) 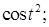 3)
3) 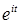 ; 4)
; 4) 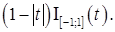 Если да, то найти соответствующее распределение.
Если да, то найти соответствующее распределение.
5.На вероятностном пространстве 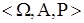 , представляющем собой отрезок
, представляющем собой отрезок  с
с  -алгеброй борелевских подмножеств и мерой Лебега, определена с.в.
-алгеброй борелевских подмножеств и мерой Лебега, определена с.в. 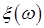 . Найти ее х.ф., если:
. Найти ее х.ф., если:  ;
;  .
.
6. Найти распределения, которым соответствуют следующие х.ф.: a)  ;
;
b)  ; c)
; c)  d)
d) 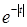 ; e)
; e) 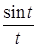 ; f)
; f) 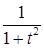 ; g)
; g) 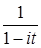 .
.
§ 9 Предельные теоремы
Здесь мы будем рассматривать последовательности  случайных величин, наблюдаемых в одном и том же опыте
случайных величин, наблюдаемых в одном и том же опыте  . Ограничимся случаем последовательности стохастически независимых с.в.
. Ограничимся случаем последовательности стохастически независимых с.в.
Классической для теории вероятностей является задача нахождения предельного распределения для последовательности сумм  где
где 
Сформулируем следующие предельные теоремы.
Теорема 1.( Закон больших чисел). Рассмотрим последовательность 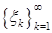 с.в., удовлетворяющих условиям:
с.в., удовлетворяющих условиям:
1. 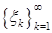 - стохастически независимы;
- стохастически независимы;
2. 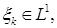
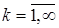 ;
;
3. 
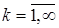 . Тогда
. Тогда 
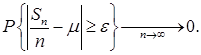
Теорема 2.( Центральная предельная). Рассмотрим последовательность 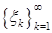 с.в., удовлетворяющих условиям:
с.в., удовлетворяющих условиям:
1. 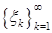 - стохастически независимы;
- стохастически независимы;
2. 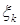 - одинаково распределены,
- одинаково распределены, 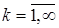 ;
;
3.  и
и 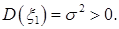
Тогда 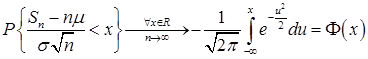 , где
, где 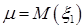 и
и  - функция Лапласа.
- функция Лапласа.
Задачи для самостоятельного решения
1. Рассмотрим последовательность 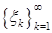 стохастически независимых и имеющих
стохастически независимых и имеющих  распределение с.в. 1) Подчиняется ли данная последовательность закону больших чисел, центральной предельной теореме? 2) Подчиняются ли закону больших чисел и центральной предельной теореме последовательности с.в.
распределение с.в. 1) Подчиняется ли данная последовательность закону больших чисел, центральной предельной теореме? 2) Подчиняются ли закону больших чисел и центральной предельной теореме последовательности с.в. 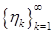 и
и  , где
, где 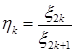 ,
, 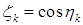 ,
, 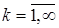 ?
?
2. Складывается 104 чисел, округленных с точностью до 10-m. Предполагая, что ошибки округления независимы и равномерно распределены в интервале  , найти пределы, в которых с вероятностью, не меньшей 0,99, будет лежать суммарная ошибка.
, найти пределы, в которых с вероятностью, не меньшей 0,99, будет лежать суммарная ошибка.
3. Доказать, что при 
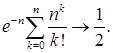
4. Вероятность некоторого события равна  в каждом из
в каждом из  независмых испытаний. Найти вероятность того, что: a) частота наступления события при
независмых испытаний. Найти вероятность того, что: a) частота наступления события при 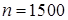 отклонится от вероятности
отклонится от вероятности 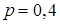 в ту или другую сторону меньше, чем на 0,02; b) число появления события будет заключено между 600 и 660; c) в каких границах находится та частота события при
в ту или другую сторону меньше, чем на 0,02; b) число появления события будет заключено между 600 и 660; c) в каких границах находится та частота события при  , вероятность отклонения которой от вероятности
, вероятность отклонения которой от вероятности  , равна 0,985? В каких границах заключено число появлений события в этой задаче? d) Сколько необходимо провести испытаний, чтобы вероятность того, что отклонение частоты от вероятности появления события в одном опыте
, равна 0,985? В каких границах заключено число появлений события в этой задаче? d) Сколько необходимо провести испытаний, чтобы вероятность того, что отклонение частоты от вероятности появления события в одном опыте 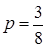 в ту или другую сторону будет меньше, чем 0,01, была равна 0,995?
в ту или другую сторону будет меньше, чем 0,01, была равна 0,995?
5. Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице не менее 3-х опечаток.
6. Вероятность того, что любой абонент позвонит на коммутатор в течение часа равна 0,01. Телефонная станция обслуживает 300 абонентов. Какова вероятность того, что в течение часа позвонят 4 абонента?
Таблица 1.
| Обозначения | Теория множеств и теория меры | Теория вероятностей | Эмпирическое значение соответствующих понятий | |||||
| G | Случайный опыт, обладающий свойством статистической устойчивости частот | Действие и наблюдение за его результатами, которые неоднозначно определяются условиями проведения опыта G. При большом числе проведений опыта частота исхода близка к некоторой постоянной для данного исхода | ||||||

| Основное(универсальное множество) | Множество исходов случайного опыта
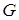
| Полный список взаимоисключающих исходов (результатов) в предположении, что опыт происходит в идеальных условиях | |||||
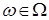
| Элемент  основного множества основного множества 
|  - исход опыта - исход опыта 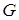
| При проведении опыта G появляется один и только один из исходов -неделим в рамках данной модели. -неделим в рамках данной модели.
| |||||
| A | Совокупность подмножеств множества 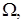 являющаяся являющаяся  -алгеброй -алгеброй
| Совокупность случайных событий | Совокупность событий (результатов), наблюдаемых при проведении опыта G. | |||||
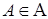
| А - элемент А , т.е. А 
| А - случайное событие (список «благоприятных» для А исходов) | Некоторый результат сл. опыта G (возможна словесная формулировка) | |||||

|  -элемент множества А -элемент множества А
| Исход  , благоприятный (благоприятствующий) событию А , благоприятный (благоприятствующий) событию А
| Если при проведении опыта G появился исход  А, то говорят, что событие А произошло в противном случае ( А, то говорят, что событие А произошло в противном случае (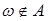 )
событие А не произошло. )
событие А не произошло.
| |||||

| Пустое множество | Невозможное событие | Событие, которое никогда не происходит при реализации данного комплекса условий | |||||

| Универсальное множество | Достоверное событие | Результат (событие), которое всегда происходит при реализации данного комплекса условий G | |||||
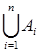
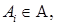
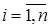
| Объединение множеств

| Объединение сл. событий  -
событие, состоящее из исходов, принадлежащих хотя бы одному из событий -
событие, состоящее из исходов, принадлежащих хотя бы одному из событий 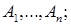
| Событие (результат), которое происходит тогда и только тогда, когда происходит хотя бы одно из событий  , т.е. , т.е.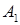 или или , или и т.д. или , или и т.д. или  . .
| |||||

| ||||||||

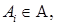
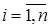
| Пересечение множеств
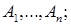
| Пересечение (произведение) сл.событий  -событие, состоящее из общих для -событие, состоящее из общих для  исходов исходов
| Событие (результат), которое происходит тогда и только тогда, когда происходят одновременно события , т.е. , т.е. 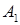 и и  , и и т.д. и , и и т.д. и  . .
| |||||

| ||||||||
 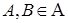
| Множество А и В не пересекаются | А,В - несовместные события | События А и В не могут происходить одновременно | |||||
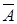
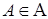
|  - дополнение множества - дополнение множества 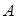 до универсального мн-ва до универсального мн-ва 
| 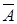 - противоположное событию А; - противоположное событию А;  -пара противоположных событий, т.е. -пара противоположных событий, т.е. 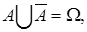  , ,
| 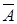 - происходит тогда и только тогда, когда не происходит А, т.е. не А; в результате опыта одно и только одно из противоположных событий происходит - происходит тогда и только тогда, когда не происходит А, т.е. не А; в результате опыта одно и только одно из противоположных событий происходит
| |||||
 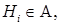 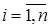
| Разбиение множества 
| Разбиение множества исходов 
| В результате опыта обязательно происходит одно и только одно из событий данного разбиения | |||||
т.е. , для , для 
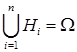
| ||||||||
АВ;
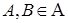
| Разность множеств А и В | Разность событий А и В | АВ происходит тогда и только тогда, когда А происходит, а В нет | |||||

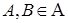
| А — подмножество В | Событие А влечет событие В | Если произошло событие А, то обязательно произошло В | |||||
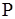
| Вероятностная мера на измеримом пространстве

|
 - вероятность случайного события - вероятность случайного события 
| Численная мера возможности появления события 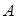 (см. стр. 7) (см. стр. 7)
| |||||
Таблица 2.
| Название модели | Обозначение модели | Распределение вероятностей (ряд распределения или плотность распределения вероятностей) | Числовые характеристики |
| Биномиальное распределение | 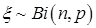

| 

| |
| Геометрическое распределение | 

| 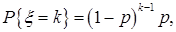
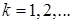
| |
| Распределение Пуассона | 

| 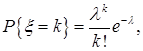

| |
| Гипергеометрическое распределение | Параметры n, N, M 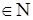 и
и 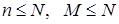
|  и
и  для для 
| |
| Равномерное распределение | 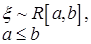
| 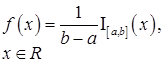
| |
| Нормальное распределение | 
| 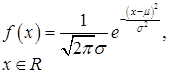
| |
| Распределение Коши | 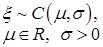
| 
| |
| Гамма распределения | 
|  гамма функция Эйлера гамма функция Эйлера
| |
| Показательное распределение | 
| 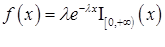
| |
| Хи-квадрат распределение | 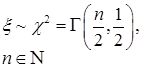
| 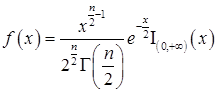
|
СОДЕРЖАНИЕ
§1. Элементы комбинаторики......................................................................3
§2. Математическая модель случайного опыта..........................................6
§3. Свойства вероятностей случайных событий. Условная вероятность
Стохастически независимые случайные события.....................................10
§4. Формула полной вероятности. Формула Байеса................................13
§5. Схема Бернулли.....................................................................................16
§6. Случайные величины............................................................................17
§7. Случайные векторы...............................................................................22
§8. Характеристическая функция случайных величин и случайного
вектора...........................................................................................................25
§9. Предельные теоремы.............................................................................26
ЛИТЕРАТУРА
1.Боровков А.А. Теория вероятностей / А.А. Боровков. - М.: Эдиториал УРСС, 1999.-472с.
2.Прохоров А.В. Задачи по теории вероятностей / А.В. Прохоров,В.Г.. Ушаков, Н.Г. Ушаков. - М.: Наука, 1986.-328с.
3.Зубков А.М. Сборник задач по теории вероятностей / А.М. Зубков, Б.А. Севастьянов, В.П. Чистяков. - М.: Наука, 1989.-320с.
Составители : Михайлова Ирина Витальевна
Баркова Лариса Николаевна
Редактор Тихомирова О.А.
– Конец работы –
Эта тема принадлежит разделу:
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ... ТЕОРИЯ ВЕРОЯТНОСТЕЙ Пособие для студентов по специальностям и...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Вектора
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов