рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- ЧАСТИННІ ПОХІДНІ n-го ПОРЯДКУ
Реферат Курсовая Конспект
ЧАСТИННІ ПОХІДНІ n-го ПОРЯДКУ
ЧАСТИННІ ПОХІДНІ n-го ПОРЯДКУ - раздел Математика, ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ З КУРСУ ВИЩА МАТЕМАТИКА ДО ТЕМИ ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ Частинні Похідні ...
Частинні похідні 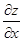 і
і  функції z=f(х;y) є деякими функціями змінних х та y і, в свою чергу, можуть мати частинні похідні і по х, і по y, які називаються частинними похідними другого порядку від функції z=f(х;y). Позначаються і визначаються похідні другого порядку так:
функції z=f(х;y) є деякими функціями змінних х та y і, в свою чергу, можуть мати частинні похідні і по х, і по y, які називаються частинними похідними другого порядку від функції z=f(х;y). Позначаються і визначаються похідні другого порядку так:
 (9.31)
(9.31)
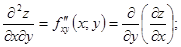 (9.32)
(9.32)
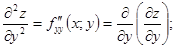 (9.33)
(9.33)
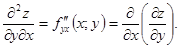 (9.34)
(9.34)
Теорема 1. Якщо функція z=f(х;y) та її частинні похідні 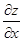 ,
,  ,
,  ,
, 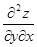 неперервні у точці М(х;y) і в деякому околі цієї точки, то у цій точці
неперервні у точці М(х;y) і в деякому околі цієї точки, то у цій точці
 =
= . (9.35)
. (9.35)
Частинні похідні другого порядку знову можна диференціювати по х та по y. При цьому отримаємо частинні похідні третього порядку, яких для функції двох змінних z=f(х;y) буде вісім:
 (9.36)
(9.36)
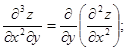 (9.37)
(9.37)
 (9.38)
(9.38)
 (9.39)
(9.39)
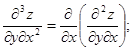 (9.40)
(9.40)
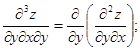 (9.41)
(9.41)
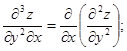 (9.42)
(9.42)
 (9.43)
(9.43)
Означення 20. Частинною похідною n-го порядку функції z=f(х;y) називається частинна похідна першого порядку від частинної похідної (n-1)-го порядку.
Приклад 14. Для функції 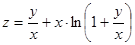 довести, що
довести, що  .
.
Знайдемо спочатку частинні похідні першого та другого порядків заданої функції:



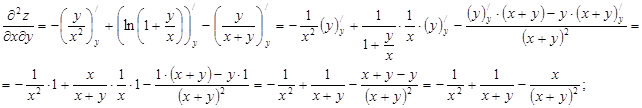


Тепер розглянемо вираз та підставимо знайдені похідні:

що і треба було довести.
Приклад 15. Знайти частинні похідні другого порядку функції 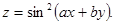
Знайдемо частинні похідні першого порядку:



А тепер знайдемо частинні похідні другого порядку:




Таким чином
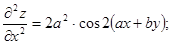
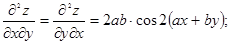
 .
.
10. ЕКСТРЕМУМ ФУНКЦІЇ z=f(х;y)
Означення 21. Точка M0(x0;y0) називається точкою локального максимуму функції z=f(х;y) якщо існує такий окіл точки M0, в якому для будь-якої точки M(x;y) (окрім самої точки M0(x0;y0)) виконується нерівність
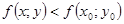 . (10.44)
. (10.44)
Означення 22. Точка M0(x0;y0) називається точкою локального мінімуму функції z=f(х;y), якщо існує такий окіл точки M0, в якому для будь-якої точки M(x;y) (окрім самої точки M0(x0;y0)) виконується нерівність
 . (10.45)
. (10.45)
Означення 23. Локальні мінімуми і максимуми функції називаються її локальними екстремумами. Точка, в якій досягається локальний екстремум функції, називається точкою локального екстремуму.
Приклад 16. Функція 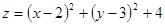 досягає у точці M0(2;3) локального мінімуму. Дійсно,
досягає у точці M0(2;3) локального мінімуму. Дійсно,  , крім того для всіх
, крім того для всіх 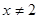 і
і  маємо
маємо 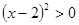 і
і 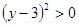 , а
, а  , тобто
, тобто  для всіх
для всіх 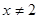 і
і  . Отже,
. Отже, 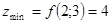 .
.
Теорема 2 (необхідні умови локального екстремуму).
Якщо диференційована функція z=f(х;y), має в точці M0(x0;y0) локальний екстремум, то виконуються рівності:
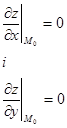 . (10.46)
. (10.46)
Означення 24. Точки, в яких виконуються рівності (6.34), або в яких 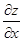 і
і  не існують, називаються критичними або стаціонарними точками для функції z=f(х;y).
не існують, називаються критичними або стаціонарними точками для функції z=f(х;y).
Теорема 3 (достатні умови локального екстремуму).
Нехай у точці M0(x0;y0) і деякому її околі функція z=f(х;y) має неперервні частинні похідні до третього порядку включно; нехай, крім того,  . Позначимо
. Позначимо  і
і  . Тоді:
. Тоді:
функція z=f(х;y) досягає в точці M0(x0;y0) локального максимуму, якщо  ;
;
функція z=f(х;y) досягає в точці M0(x0;y0) локального мінімуму, якщо  ;
;
функція z=f(х;y) не має в точці M0(x0;y0) локального екстремуму, якщо 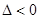 ;
;
функція z=f(х;y) може мати і може не мати в точці M0(x0;y0) локального екстремуму, якщо ∆=0 (в цьому випадку потрібно провести додаткові дослідження).
Приклад 17. Дослідити на екстремум функцію 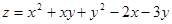 .
.
Спочатку знайдемо критичні точки, для чого використаємо необхідні умови (6.34) локального екстремуму.
Так як 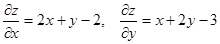 , то маємо систему рівнянь
, то маємо систему рівнянь
 розв’язком якої є
розв’язком якої є  .
.
Отже, точка  – критична точка.
– критична точка.
Тепер перевіримо для цієї точки достатні умови локального екстремуму.

Маємо  і
і 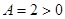 , а отже, в точці
, а отже, в точці  задана функція має локальний мінімум і
задана функція має локальний мінімум і  .
.
Приклад 18. Дослідити на екстремум функцію 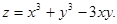
Знайдемо критичні точки, використовуючи необхідні умови локального екстремуму.
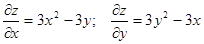 .
.
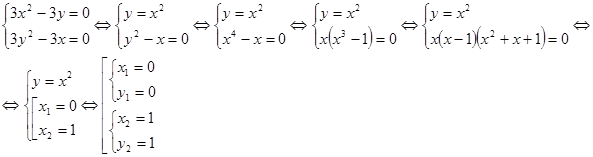
і, отже, маємо 2 критичні точки М1(0;0) і М2(1;1).
Знайдемо частинні похідні другого порядку 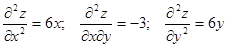 .
.
умов локального екстремуму.
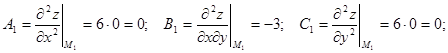
 і згідно з теоремою 3 у точці М1(0;0) задана функція локального екстремуму не має.
і згідно з теоремою 3 у точці М1(0;0) задана функція локального екстремуму не має.
Тепер розглянемо, чи виконуються достатні умови локального екстремуму у точці М2(1;1).

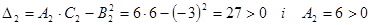 .
.
Згідно з теоремою 3 у точці М2(1;1) задана функція досягає локального мінімуму і  .
.
Приклад 19. Дослідити на екстремум функцію  .
.
Згідно з теоремою 2 необхідні умови існування локального екстремуму виглядять так:
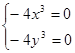 .
.
Розв’язком цієї системи рівнянь є 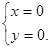
Отже, критична точка М0(0;0).
Знайдемо другі частинні похідні:

Тоді 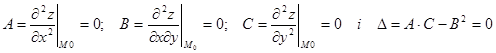 .
.
Згідно з теоремою 3 потрібні додаткові дослідження. Проведемо їх:
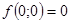 а для всіх
а для всіх 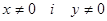
 ; отже
; отже
 , тобто
, тобто 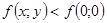 для всіх
для всіх 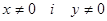 . Згідно з означенням 20 у точці М0(0;0) задана функція досягає локального максимуму і
. Згідно з означенням 20 у точці М0(0;0) задана функція досягає локального максимуму і 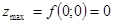 .
.
– Конец работы –
Эта тема принадлежит разделу:
ДО ВИКОНАННЯ САМОСТІЙНОЇ РОБОТИ З КУРСУ ВИЩА МАТЕМАТИКА ДО ТЕМИ ДИФЕРЕНЦІАЛЬНЕ ЧИСЛЕННЯ ФУНКЦІЇ БАГАТЬОХ ЗМІННИХ
ДЕРЖАВНИЙ ВИЩИЙ НАВЧАЛЬНИЙ ЗАКЛАД... УКРАЇНСЬКИЙ ДЕРЖАВНИЙ ХІМІКО ТЕХНОЛОГІЧНИЙ УНІВЕРСИТЕТ... МЕТОДИЧНІ ВКАЗІВКИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ЧАСТИННІ ПОХІДНІ n-го ПОРЯДКУ
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов