ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

Содержание

ВВЕДЕНИЕ_______________________________________________________________ 3

1. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ_____________________________________

1.1. Векторы в евклидовом пространстве____________________________________

1.2. Проекция вектора____________________________________________________

1.3. Декартовы прямоугольные координаты_________________________________

1.4. Координатное представление векторов__________________________________

1.5. Операции над векторами, заданными в координатной форме______________

1.6. Скалярное произведение векторов_____________________________________

1.6.1. Свойства скалярного произведения:__________________________________________

1.6.2. Скалярное произведение векторов, заданных координатами____________________

1.6.3. Угол между векторами______________________________________________________

1.6.4. Условия коллинеарности и перпендикулярности векторов______________________

1.7. Векторное произведение двух векторов_________________________________

1.7.1. Свойства векторного произведения__________________________________________

1.7.2. Координатная форма записи векторного произведения_________________________

1.8. Смешанное (векторно - скалярное) произведение векторов________________

1.8.1. Свойства смешанного произведения__________________________________________

1.8.2. Координатная форма записи смешанного произведения________________________

1.9. Двойное векторное произведение трех векторов__________________________

1.10. Вопросы для самопроверки__________________________________________

2. ПОНЯТИЕ ОБ УРАВНЕНИЯХ ЛИНИЙ И ПОВЕРХНОСТЕЙ________________

3. ПРЯМАЯ ЛИНИЯ_______________________________________________________

3.1. Параметрические и канонические уравнения прямой____________________

3.2. Общее уравнение прямой на плоскости_________________________________

3.4. Уравнение пучка прямых на плоскости_________________________________

3.5. Решение типовых задач к разделу 3____________________________________

3.6. Задачи для самостоятельной работы____________________________________

3.7. Вопросы для самопроверки к разделу 3_________________________________

4. ПРЕОБРАЗОВАНИЕ КООРДИНАТ НА ПЛОСКОСТИ______________________

4.1. Параллельный перенос осей координат_________________________________

4.2. Поворот осей координат______________________________________________

5. КРИВЫЕ ВТОРОГО ПОРЯДКА__________________________________________

5.1. Окружность_________________________________________________________

5.2. Эллипс_____________________________________________________________

5.3. Гипербола__________________________________________________________

5.4. Директрисы эллипса и гиперболы______________________________________

5.5. Парабола___________________________________________________________

5.6. Уравнения эллипса, гиперболы и параболы в полярных координатах_______

5.7. Решение типовых примеров___________________________________________

5.8. Задачи для самостоятельной работы____________________________________

Ответы к 5.8____________________________________________________________

5.9. Вопросы для самопроверки___________________________________________

Ответы к 5.9____________________________________________________________

6. ПЛОСКОСТЬ И ПРЯМАЯ В ПРОСТРАНСТВЕ_____________________________

6.1. Общее уравнение плоскости___________________________________________

6.2. Уравнение в отрезках________________________________________________

6.3. Векторное и нормальное уравнение плоскости___________________________

6.4. Расстояние от точки до плоскости______________________________________

6.5. Взаимное расположение двух плоскостей_______________________________

6.6. Пучок плоскостей____________________________________________________

6.7. Уравнение плоскости, проходящей через три заданные точки______________

6.8. Уравнение прямой в пространстве_____________________________________

6.8.1. Общие уравнения прямой___________________________________________________

6.8.2. Параметрические и канонические уравнения прямой____________________________

6.8.3. Уравнения прямой, проходящей через две заданные точки______________________

6.9. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых

6.10. Угол между прямой и плоскостью. Условия параллельности и перпендикулярности прямой и плоскости___________________________________________________________________

6.11. О решение задач аналитической геометрии на плоскость и прямую________

6.11.1. Примеры решения типовых задач___________________________________________

6.11.2. Задачи для самостоятельного решения______________________________________

6.11.3. Вопросы для самопроверки________________________________________________

Ответы к 6.11.2__________________________________________________________________

Ответы к 6.11.3__________________________________________________________________

7. КРАТКОЕ ОПИСАНИЕ РАЗЛИЧНЫХ ВИДОВ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА

7.1. Распадающиеся поверхности__________________________________________

7.2. Цилиндрические поверхности_________________________________________

7.3. Конусы второго порядка______________________________________________

7.4. Эллипсоиды и гиперболоиды__________________________________________

7.5. Параболоиды_______________________________________________________

7.6. Задачи для самостоятельной работы____________________________________

КОНТРОЛЬНОЕ ЗАДАНИЕ________________________________________________

Контрольные вопросы___________________________________________________

Ответы к контрольному заданию__________________________________________

Ответы________________________________________________________________

Литература____________________________________________________________ 52

Введение

Это пособие представляет собой курс лекций и практических занятий для самостоятельной работы студентов. Наряду с традиционной математикой это пособие содержит основные сведения применения линейной алгебры к исследованию и построению кривых и поверхностей второго порядка, а также приложение квадратичной формы к задачам аналитической геометрии.

Элементы векторной алгебры

Векторы в евклидовом пространстве

   

Решение.

   

Проекция вектора

   

Декартовы прямоугольные координаты

Ось Oxназывают осью абсцисс, ось Oy - осью ординат и ось Oz-осью аппликат. Координатные оси Ox, Oy, Oz, взятые попарно, определяют три взаимно… Декартова система координат позволяет связать с каждой точкой P пространства, в котором выбраны три не лежащие в одной…

Координатное представление векторов

Разложим произвольный вектор трехмерного пространства по ортам. Для этого построим вектор , равный вектору . Из точки Мопустим перпендикуляр на…    

Скалярное произведение векторов

, (1.6.1) где - угол между векторами и (рис.1.10).  

Скалярное произведение векторов, заданных координатами

, , (1.6.2.1) Далее, используя свойство скалярного произведения имеем: (1.6.2.2)

Угол между векторами

(1.6.3.1) Если векторы и заданы координатами и , то формула (1.6.3.1) запишется в… (1.6.3.2)

Условия коллинеарности и перпендикулярности векторов

, (1.6.4.1) где скалярный множитель >0, если векторы и имеют одинаковые направления и… Пусть заданны два вектора в координатной форме: и .

Векторное произведение двух векторов

или (1.7.1) и определяемый следующими тремя условиями: 1) Модуль вектора равен площади параллелограмма, построенного на векторах и (после совмещения их начал), т.е.

Свойства векторного произведения

2). , т.е. векторное произведение антикоммутативно. 3). , т.е. векторное произведение обладает распределительным свойством. 4).

Координатная форма записи векторного произведения

, (1.7.2.1) где - координаты вектора в прямоугольной системе координат Oxyz (т.е. проекции… Координаты векторного произведения в прямоугольной системе координат можно найти разложив определитель (1.7.2.1) по…

Смешанное (векторно - скалярное) произведение векторов

, (1.8.1) где первых два вектора перемножаются векторно, а их произведение умножается… Смешанное произведение трех векторов - величина скалярная.

Свойства смешанного произведения

а). Если перемножаемые вектора переставлять в круговом порядке: б). Если поменять местами знаки векторного и скалярного умножения:

Координатная форма записи смешанного произведения

(1.8.2.1) Замечание 1.При помощи смешанного произведения можно вычислить объем…

Двойное векторное произведение трех векторов

(1.9.1) Так как оно часто используется в приложениях, покажем, что его вычисление… (1.9.2)

Вопросы для самопроверки

2. Какие векторы называются коллинеарными, компланарными? 3. Основные операции над векторами. 4. Что называется проекцией вектора на заданную ось? Свойство проекций.

Понятие об уравнениях линий и поверхностей

Уравнение F(x,y)=0 называется общим уравнением линии в системе координат XOY, если ему удовлетворяют координаты любой точки M, принадлежащей линии… Линией первого порядка на плоскости называется множество точек, координаты… (2.1)

ПРЯМАЯ ЛИНИЯ

Параметрические и канонические уравнения прямой

Пусть -текущая точка на прямой l, т.е. точка, пробегающая всю прямую, и пусть Oxyz - прямоугольная декартова система.    

Общее уравнение прямой на плоскости

(3.2.1) где , , Уравнение Ах+Ву+С=0 называется общим уравнением прямой. Желательно запомнить, что вектор , проекции которого на оси…

Уравнение пучка прямых на плоскости

Если точка задана своими координатами, то уравнение пучка может быть записано в виде либо , либо . Если же точка задана точкой пересечения прямых и… (3.4.1) где - действительное число.

Решение типовых задач к разделу 3

3.5.1. Найти уравнение окружности радиуса R с центром в точке C(a,b)

Решение. По определению окружности расстояние любой точки M(x,y), лежащей на окружности, от ее центра C(a,b) равно длине радиуса R, т.е. CM=R.

Найдем длину отрезка CM и выразим равенство CM=R с помощью текущих координат точки M:

3.5.2. Найти точки пересечения линий 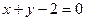и

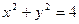
Решение. Система уравнений

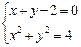имеет два решения: и , следовательно, данные линии имеют две общие точк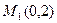и и .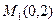

3.5.3. Составить уравнение прямой линии, образующей с осью Ох угол 60° и пересекающей ось Оу в точке (0,-2). Выяснить, проходит ли эта прямая через точки А(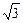,1) и В (2,5)

Решение. Из условия задачи следует, что начальная ордината b=-2, угловой коэффициент 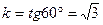, следовательно, по формуле (3.1.7) имеем .

Подставляя в искомое уравнение прямой координаты точки А вместо текущих координат, получим 1=3-2, т.е. 1=1.

Прямая проходит через точку А(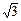,1).

Аналогично, подставляя в уравнение координаты точки B, получим: .

Прямая не проходит через точку В.

3.5.4. Уравнениепривести к уравнению с угловым коэффициентом

Решение. Данное уравнение решим относительно , получим уравнение .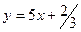

Отсюда видно, что , .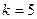

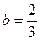3.5.5. Написать уравнение прямой, проходящей через данные точки
А(2,-5) и В(1,3)

Решение. Используя формулу (3.8) запишем уравнение данной прямой

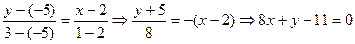
3.5.6. Написать уравнение прямой проходящей через точку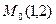

1. Параллельно вектору .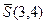

2. Перпендикулярно вектору .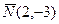

Решение.

1. Используя каноническое уравнение прямой (3.5), имеем или .

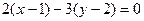2. Используем уравнение (4.1): . Имеем или .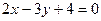

3.5.7. Найти координаты M(x,y,z), делящей отрезок M₁M₂ в отношении 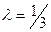, если M₁(1,2,3), M₂(3,9,-2)

Решение. Используем формулы деления отрезка в заданном отношении .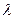

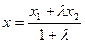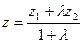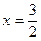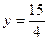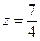, , , , , (3.5.7)

3.5.8. Найти угол между прямыми и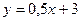

Решение. По формуле (3.3.1) получим 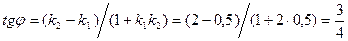, где , , .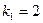

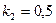Здесь угол отсчитывается от прямой .

3.5.9. Выбрать значение коэффициента прямой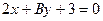

таким, чтобы эта прямая была:

1. Параллельна прямой .

2. Перпендикулярна прямой .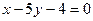

Решение.

1. Используя условие параллельности прямых, получим
, .

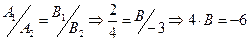2. Используя условие перпендикулярности прямых, получим

, .

3.5.10. Найти уравнение прямой, проходящей через точку пересечения прямых 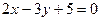и , а также:
а). точку 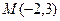, б). перпендикулярно прямой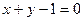

Решение.

a) Используем уравнение пучка прямых, проходящих через точку пересечения данных прямых 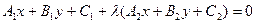. Имеем 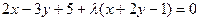. Число 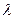найдем из условия, что прямая должна проходить через точку 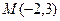: Подставляя найденное значение 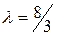в уравнение пучка, получим

.

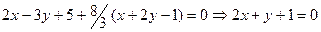b) Используя условия перпендикулярности прямых, можем записать . Подставляя в уравнение пучка, получим .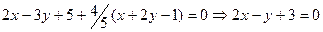

Задачи для самостоятельной работы

1. . 2. . 3. .

Вопросы для самопроверки к разделу 3

3.7.1. Какие виды задания прямой на плоскости Вы знаете?

3.7.2. Напишите параметрическое уравнение прямой в векторной и координатной формах.

3.7.3. Найти координаты точки С пересечения медиан треугольника, вершины которого находятся в точках 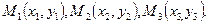(В механике доказывается, что С является центром тяжести однородного треугольника).

Указание: использовать формулы (3.5.7).

3.7.4. Исходя из уравнения прямой с угловым коэффициентом y=kx+b, при различных значениях параметров k и b записать:

а) уравнение прямой, проходящей через начало координат;

б) уравнение прямой, параллельной оси Ох;

в) уравнение прямой, параллельной оси Оу;

д) уравнение прямой, совпадающей с осью Оу.

3.7.5. Всякое ли алгебраическое уравнение первой степени определяет прямую линию? Запишите общее уравнение прямой.

3.7.6. Пусть дано общее уравнение прямой: Ах+Ву+С=0

Привести это уравнение к уравнению с угловым коэффициентом.

3.7.7. Написать уравнение прямой, проходящей через заданные точки 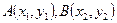. Какая связь между уравнением прямой, проходящей через две точки, и каноническим уравнением прямой, проходящей через эти точки.

3.7.8. Выведите условие, при котором три данные точки лежат на одной прямой.

3.7.9. Пусть даны прямые 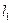и 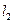. Дайте определение угла между двумя пересекающимися прямыми. Условия параллельности и перпендикулярности двух прямых

3.7.10. Записать формулы нахождения угла между двумя прямыми, если прямые заданы уравнениями:

1) ;

2)

3)

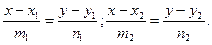
3.7.11. Определить расстояние между двумя параллельными прямым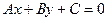и

и .

Ответы к 3.6

3.6.1.

3.6.2.

3.6.3.

3.6.4. и ;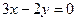

3.6.5.

3.6.6.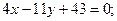

3.6.7.

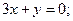
3.6.8. 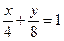и ;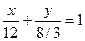

3.6.9.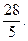

Ответы к 3.7

3.7.3.

3.7.4. а) при b=0 => y=kx;

б) при k=0 => y=b;

в) при k=b=0 => y=0;

г) x=a;

д) x=0;

3.7.7. - есть направляющий вектор прямой, который либо параллелен прямой, либо принадлежит ей.

3.7.8.

3.7.10. 3)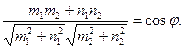

3.7.11. Указание. Найти абсциссу точки пересечения второй прямой с осью Ox и использовать формулу (3.3.3). Ответ:

4. Преобразование координат
на плоскости

Одни и те же линии в разных системах координат имеют разные по сложности уравнения. Поэтому, чтобы лучше представить себе линию или фигуру, прибегают к замене систем координат.

Параллельный перенос осей координат

   

Поворот осей координат

   

Кривые второго порядка

Любое уравнение второго порядка вида Ах2+2Вocy+Сy2+Ех+Dх+F=0 определяет на плоскости одну из след. кривых: окружность, эллипс, гиперболу, параболу или, в особых случаях, пару прямых или точки.

Мы не будем доказывать это утверждение, а приведем лишь канонические уравнения перечисленных линий второго порядка и их геометрические изображения.

Окружность

                   

Эллипс

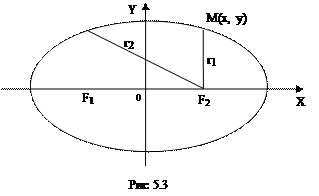
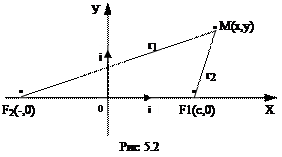Эллипс - геометрическое место точек на плоскости, для каждой из которых сумма расстояний до двух данных точек F₁ и F₂ той же плоскости, называемых фокусами эллипса, есть величина постоянная, равная 2а и большая, чем расстояние между фокусами 2с. Выведем уравнение эллипса, исходя из данного определения. Выберем систему координат как показано на рис 5.2

 

 

 

(Расстояния любой точки M(x,y) эллипса до фокусов называются ее фокальными радиусами. Пусть M(x,y) - произвольная точка эллипса, числа r₁ и r₂ –фокальные радиусы т. M:

r₁ =F₁M; r₂=F₂M; r₁ +r₁=2а (см. рис.5.2), тогда r₁= а -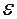х; r₁ = а +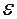х (5.2.1), где 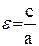, а - большая полуось эллипса, с- половина расстояния между фокусами. Формулы (5.2.1) линейно выражают фокальные радиусы любой точки эллипса через ее абсциссу.)

r₁ = F₁M =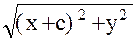; r₂ = F₂M =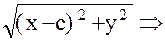

F₁M + F₂M =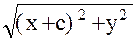+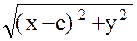= 2а

Это уравнение эллипса приведем к более простому виду: возводя дважды это уравнение в квадрат и преобразуя его, получим:

x² + 2xc + c² + y² = 4a² - 4a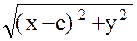+ x² - 2xc² + y²;

xc - a² =-a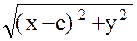; x²c² - 2xca² + a⁴ = a²(x² - 2xc + c²) + a²y;

x²(c² - a²) - a²y² = a²c² - a⁴; x²(a² - c²) + a²y² = a²(a² - c²); x²b² + a²y² = a²b²,

где положили а² - с² = b². Деля обе части последнего равенства на a²b², получим каноническое уравнение эллипса; 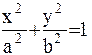(5.2.2)

Как видно из этой формулы эллипс симметричен относительно осей OX и OY, т.к. вместе с точкой (x,y) ему принадлежат и точки (-x,-y), (-x, y), (x, -y). Точки пересечения с осями называются вершинами эллипса и равны x = 0; y =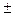b; y = 0; x =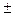a (5.2.3)

Определение: Эксцентриситетом эллипса называется отношение расстояния между фокусами к длине большой оси.

Обозначив эксцентриситет через 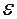, получим 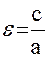(5.2.4)

Эксцентриситет характеризует форму эллипса. Эксцентриситет эллипса содержится в промежутке (0, 1).

 

 

 

Гипербола

Поступая также, как и в случаи эллипса, получим каноническое уравнение гиперболы: (5.3.1), где в2 = с2 - а2 Гипербола изображена на рис 5.4.  

Директрисы эллипса и гиперболы

                …  

Парабола

Каноническое уравнение параболы: y2=2рх, (5.5.1) где р- расстояние от фокуса до директрисы. Парабола показана на рис. 5.7

Решение типовых примеров

Пример 1. Составить каноническое уравнение эллипса, зная, что большая его ось 2а=10 и эксцентриситет .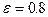

Решение: По формуле (5.2.4) с= аe =5Ч0.8 = 4, а b находим из равенства b² = а² - с² = 25 - 16 = 9b =3. Подставляя найденные значения а=5, b=3 в уравнение (5.2.2), получим искомое уравнение эллипса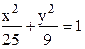

Пример 2. Написать уравнение гиперболы по данной полуоси а = 1 и полуфокусному расстоянию с = 2.

Решение: Из равенства а² + b² = с² найдем полуось b: 1 + b² = 4 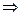b =.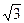

Искомое уравнение гиперболы будет иметь вид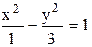

Пример 3. Найти координаты фокуса и уравнение директрисы параболы х = -5у²

Решение: Перепишем уравнение так: 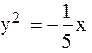и, сравнивая его с уравнением у² = -2рх, получим . Координаты фокуса и уравнение директрисы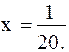

Пример 4. Найти координаты вершины параболы, заданной уравнением х=у²+4у+1. Написать уравнение оси симметрии.

Решение: Найдем координаты вершины параболы: х = (у² + 4у + 4) - 4 + 1 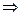х+3=(у+2)². Следовательно вершина параболы лежит в точке (-3,-2).

Уравнение оси параболы у = -2.

Пример 5. Найдите координаты точки М до поворота осей, если после поворота их на 135⁰ точка М имеет координаты (2,-3).

Решение: По формулам (4.2.1) преобразования координат получим:

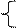х= 2 cos135⁰ - (-3) sin135⁰

y= 2 sin135⁰ +(-3) cos135⁰ ,

отсюда 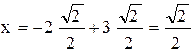, , 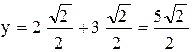следовательно, координаты до поворота осей .

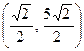Задачи для самостоятельной работы

а) 2x2+2y2+6x-3y-8=0 в) x2+y2-2y+1=0 с) x2+y2+2x+10=0

Ответы к 5.8

Решение: 2x2 + 2y2 + 6x - 3y - 8 = 0 x2 + y2 + 3x-y - 4 = 0 в) Точка С(0,1);

Вопросы для самопроверки

а) оставить ось абсцисс без изменения, переменить направление на оси ординат; б) за ось абсцисс принять прежнюю ось ординат и за ось ординат - прежнюю ось… 2. Как нужно изменить систему координат, чтобы одновременно абсциссы всех точек уменьшились на три единицы, а ординаты…

Ответы к 5.9

б) x=y1; y=x1; 2. Перенести начало координат в точку О1(3,-3). 3. Окружность.

Плоскость и прямая в пространстве

Общее уравнение плоскости

Уравнение в отрезках

Пусть в уравнении Ax+By+Cz+D = 0 , A¹0 , B¹0 , C¹0 , D¹0,

т.е. плоскость пересекает все три оси координат и не проходит через начало.

Преобразуем уравнение следующим образом: Ax + By + Cz = -D

x/(-D/A) + y(-D/B) + z(-D/C) = 1, обозначив a = (-D/A); b = (-D/B); c = (-D/C), будем иметь
x/a+y/b+c/z=1 (6.2.1)

Уравнение (6.2.1) называется уравнением плоскости в отрезках.

Векторное и нормальное уравнение плоскости

Рис. 6.2  

Расстояние от точки до плоскости

Теорема: Расстояние от точки M(x0,y0) до плоскости p, данной своим нормальным уравнением (6.3.5) равно модулю числа, получаемого, если в левую часть… Если плоскость p задана общим уравнением (6.1.2), то d =ôAx0+By0+Cz0+Dô/

Взаимное расположение двух плоскостей

и A2x + B2y + C2z + D2 = 0 (6.5.2) образуют две пары вертикальных двугранных углов. Углом между плоскостями будем называть любой из двух смежных двугранных углов. Один из них равен углу j между…

Пучок плоскостей

(A1x + B1y + C1z + D1) + l(A2x + B2y + C2z + D2) = 0, где l - действительный параметр. Уравнением пучка плоскостей удобно пользоваться при решении многих задач аналитической геометрии.

Уравнение плоскости, проходящей через три заданные точки

Пусть M(x,y,z) – произвольная точка искомой плоскости (рис. 6.3) . Рис. 6.3

Уравнение прямой в пространстве

В пространстве, так же как и на плоскости, одну и ту же прямую можно определить разными по форме уравнениями.

Рассмотрим несколько случаев.

Общие уравнения прямой

Прямую в пространстве можно рассматривать как линию пересечения двух плоскостей:

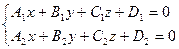(6.8.11)

Параметрические и канонические уравнения прямой

      Составим уравнение прямой l. Возьмём на прямой произвольную точку М(x,y,z) и проведём радиус-векторы =(x0,y0,z0) и…

Уравнения прямой, проходящей через две заданные точки

Подставив в уравнения (6.8.2.4.) m = x2-x1, n = y2 - y1, p = z2 - z1, x0 = x1, y0 = y1, z0 = z1, получим (x - x1)/(x2 - x1) = (y - y1)/(y2 - y1) =… Это уравнение прямой, проходящей через две данные точки. Замечание.1. Три точки М1 ,М2 ,М3 лежат на одной прямой, если выполняется условие (x3 - x1)/(x2 - x1) = (y3 - y1)/(y2…

Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых

(x-x1)/m1=(y-y1)/n1=(z-z1)/p1 (6.9.1) (x-x2)/m2=(y-y2)/n2=(z-z2)/p2 (6.9.2) Определение. Углом между двумя прямыми l1 и l2 называется угол между их направляющими векторами (m1,n1,p1) и…

О решение задач аналитической геометрии на плоскость и прямую

Чтобы научиться решать задачи на плоскость и прямую надо основательно усвоить разделы линейной алгебры, особенно теорию определителей, методы исследования и решения систем линейных уравнений; элементы векторной алгебры: понятие о векторах, действие над ними, скалярное, векторное и смешанное произведения.

Примеры решения типовых задач

Пример 1.Привести к нормальному виду уравнение плоскости 2x + 3y - 6z + 14 = 0

Решение. Из (6.3) с использованием формулы (6.3.8) находим l = -1/7.

Нормальное уравнение данной плоскости имеет вид

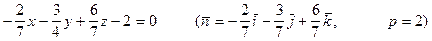
Пример 2.Найти расстояние от точки М₁(1,2,3) до плоскости 2x + y - 3z + 5 = 0

Решение. Из (6.4.) с использованием формулы (6.4.2) находим

Пример 3.От общего уравнения прямой перейти к каноническому.

Решение. Исключим из системы

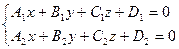
переменную x и выразим z через y.

Результат этого действия обозначим через z=(y-y₀)/n₁ (y₀,n₁-числа). Далее из этой же системы исключим y и выразим z через x; пусть этот результат будет 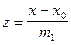(x₀, m₁ - числа).

После этого получим каноническое уравнение прямой в таком виде:

(x-x₀)/m₁ = (y-y₀)/n₁ = z/1

Вывод: данная прямая проходит через точку М₀ (x₀, y₀ ,0) в направлении вектора
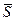(m₁,n₁,1)

Пример 4.Найти проекцию прямой (x-1)/2 = (y+1)/3 = (z-2)/-1 на плоскость 2x-3y-4z+5=0. Уравнения проекции привести к каноническому виду.

Решение. Запишем уравнение данной прямой в виде уравнения двух плоскостей

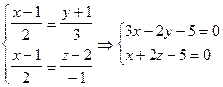
Далее, записываем уравнение пучка плоскостей (6.6): 3x - 2y – 5 + l(x + 2z - 5) = 0. Выбираем из пучка плоскость, перпендикулярную к плоскости 2x - 3y - 4z + 5 = 0.

Для этого используем условие перпендикулярности двух плоскостей (6.5.5)

2(3 + l) + (-3)(-2) + (-4)2l = 0 Þ 12 - 6l=0 Þ l = 2

Подставляя l = 2 в уравнение пучка, находим уравнение проектирующей плоскости:

5x - 2y + 4z - 15 = 0

Таким образом, искомая проекция определяется уравнениями

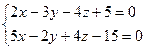
Остаётся эти уравнения привести к каноническому виду. Рекомендуется сделать самостоятельно, используя метод примера 3.

Ответ: (x - 5)/20 = (y - 5)/28 = (-7)/11

Задачи для самостоятельного решения

2. Составить уравнение плоскости, проходящей через ось Оy и точку (2, -1, 3). Найти углы, образуемые её нормалью с осями координат. 3. Найти угол между плоскостями 3x - 3y - z + 1 = 0 и x + 2y - 3z + 4 = 0 4. Указать взаимное расположение прямых

Вопросы для самопроверки

2. Записать уравнение плоскости, проходящей через точку М(x0,y0,z0) с вектором нормали (A,B,C) в векторной и координатной формах. 3. Написать каноническое уравнение плоскости. 4. Пусть прямая задана в виде (x - x0)/m = (y - y0)/n = (z - z0)/p.

Ответы к 6.11.2

2. 3x - 2z = 0; , cosb = 0, 3. 4. Прямые параллельны

Ответы к 6.11.3

2. Ax + By + Cz + D = 0; = -Þ (,(-)) = 0 4. Эта система определяет прямую, перпендикулярную к оси Оx. Прямая лежит в… 5. Эта прямая проходит через начало координат.

Краткое описание различных видов поверхностей второго порядка

В аналитической геометрии поверхность рассматривается как множество точек в пространстве. Уравнением поверхности называется такое уравнение между переменными x, y, z,… Следовательно, если известно уравнение поверхности

Распадающиеся поверхности

Пусть F(x,y,z) есть произведение двух многочленов первой степени:

F(x,y,z)=(A₁x+B₁y+C₁z+D₁)(A₂x+B₂y+C₂z+D₂) (7.1.1.),

то поверхность распадается на пару плоскостей: Ax₁+B₁y+C₁z+D₁=0 и Ax₂+B₂y+C₂z+D₂=0.

Цилиндрические поверхности

F(x,y)=0 (7.2.1.) Кривая, определяемая уравнением (7.2.1.) в плоскости Oxy, является…

Конусы второго порядка

(7.3.1.) Это уравнение и система координат, в которой данный конус задается, называются…

Эллипсоиды и гиперболоиды

(7.4.1.) (рис.7.5) рис.7.5.

Параболоиды

- для эллиптических параболоидов, (7.5.1.) -для гиперболических параболоидов, (7.5.2.) при этом p и q - положительные числа («параметры параболоидов»).

Задачи для самостоятельной работы

Приложения квадратичных форм (часть I, 5.3), преобразование координат (часть II, 4.1-4.2) 1. Найти тип и каноническое уравнение поверхности второго порядка. x2+2xy+6xz+5y2+2yz+z2=6

Контрольное задание

1. Упростить выражение:x = 2(- 2) + 6

2. Заданы вершины треугольника А(-1, -2, 4), B(-4, -1, 2) и C(-5, 4, -6); BD- его высота. Найти координаты точки D (использовать скалярное произведение двух векторов ).

3. Сила F = 2 i - 4 j +5 k приложена к точке А (4, -2, 3). Определить момент этой силы относительно точки О(3, 2, -1).

4. Даны три силы: 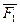(2, -1, -3), (3, 2, -1) и (-4, 1, 3), приложенные к точке А(-1, 4, 2). Определить величину и направляющие косинусы момента равнодействующих этих сил относительно точки О(2, 3, -1).

5. Заданы прямая l: x - 1/2 = y/1 = z + 1/0 и точка М(0, 1, 2).

1.написать уравнение плоскости, проходящей через точку М перпендикулярно прямой l.

2.написать уравнение плоскости, проходящей через прямую l и точку М.

6. Определить, как расположена прямая относительно эллипса: пересекает, касается или проходит вне его, если прямая и эллипс заданы уравнениями:

2 x - y - 3 = 0, x²/16 + y²/9 = 1

7. Написать уравнение гиперболы, если известно, что ее фокусами являются точки
F1(-3, -4) и F2( 3, 4), а расстояние между директрисами равно 3.6.

8. Написать уравнение параболы, если известны фокус F(4, 3) и директриса d: y + 1 = 0.

9. Записать уравнение кривой x² + y² =ax в полярной системе координат.

10. Определить, какие геометрические образцы определяются заданными уравнениями:

а) z + 5 = 0

б) ( x - 2 )² + y² + ( z + 1 )² = 16

в) x² + 2y² + 2z² + 7 = 0

г) x² - 4z² = 0

Контрольные вопросы

1. Дайте определение коллинеарности и компланарности двух векторов.

2. Операции над векторами, заданными в координатной форме. Найдите координаты суммы векторов: (1, 2, -3), (0, -2, 5), 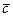(4, 0, -2)

3. Дайте определение скалярного произведения. Укажите физический смысл скалярного произведения двух векторов.

4. Основные свойства скалярного произведения. Распространяется ли скалярное произведение на три и больше число векторов?

5. Запишите скалярное произведение в координатной форме.

6. Найдите углы, образуемые вектором (4, 0, -3) с осями координат, т.е. с векторами 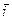(1, ,0, 0), (0, 1, 0), 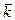(0, 0, 1).

7. Условия коллинеарности и перпендикулярности векторов.

8. Дайте определение векторного произведения. Основные свойства. Векторное произведение в координатной форме.

9*. Доказать, что [-, +] =2 [, ] и выяснить геометрический смысл этого тождества.

10*. Вектор [, [,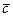]] называется двойным вектором произведением заданных векторов. Доказать, что справедливо равенство [, [,]] = (,) - (, ).

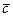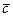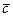11.* Доказать основное алгебраическое свойство смешанного произведения: циклическая перестановка векторов не меняет его величины, т.е.

[, ]= [,]= [,]

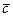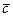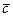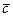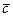[, ]=,,. Что означает эта запись?

12. Виды задания прямой на плоскости.

13. Прямая l задана точкой M0 (x0, y0) и нормальным вектором 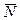(A, B).

1. написать уравнение прямой, привести его к общему виду.

2. привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.

14. Прямая l задана точкой M0 (x0, y0) и направляющим вектором 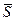(m, n). Написать уравнение прямой, привести к общему виду..

15. Прямая l задана двумя своими точками M1 (x1, y1) и M2 (x2, y2). Написать уравнение прямой.

16. Заданы прямая l и точка M. Требуется:

1. вычислить расстояние от точки M до прямой.

2. написать уравнение прямой l1, проходящей через точку М перпендикулярно прямой l.

3. написать уравнение прямой l1, проходящей через точку М параллельно заданной прямой l.

17. Виды задания прямой в пространстве.

18. Написать уравнение плоскости Р, проходящей через точки M0(x0, y0, z0) и
M1(x1, y1, z1) параллельно вектору (x, y, z).

19. Прямая l задана общим уравнениями

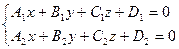
Написать каноническое уравнение этой прямой.

20. Заданы плоскость Р и точка М0. Написать уравнение плоскости Р1, проходящей через точку М0, параллельно плоскости Р. (P: Ax + By + Cz + D= 0; M0 (x0, y0, z0)).

21. Доказать что прямые

l1: 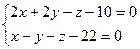и l2: (x + 7)/3 = (y - 5)/-1 = (z - 9)/4

параллельны.

22. Написать уравнение гиперболы с полуосями a и b и центром в точке С(x0, y0), если известно, что ее действительная и мнимая оси параллельны осям Ox и Oy соответственно.

23. Из фокуса параболы y²=12x под острым углом a к оси OX направлен луч света, причем tg a = 3/4. Написать уравнение прямой, на которой лежит луч, отраженный от параболы.

24. Вывести уравнение прямой в полярной системе координат, если:

a) прямая проходит через полюс;

б) прямая не проходить через полюс.

25. Показать, что параметрические уравнения x = a cos t y = a sin t t Î [0.2p], определяют окружность x² + a² = a².

26. Основные типы поверхности второго порядка.

27. Приведение поверхностей второго порядка к каноническому виду.

Ответы к контрольному заданию

2. (-2, 0, 2) 3. 4+ 3+ 4 4. , cos a = 1/, cos b = -4/, cos c= -7/

Ответы

3. Пусть под действием некоторой постоянной во величине и направлению силы F материальная точка сместилась прямолинейно по вектору АО = а, то угол между этими векторами a, тогда

 

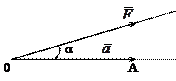
работа A == ½½½½cos a=½½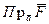. Если d = 0 .

Следовательно направление силы совпадает с направлением перемещения, т.е.
A =||||.

11. [, ]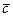=,, 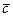(результат не зависит от того, как расставить квадратичные скобки в правой части. Это вытекает из основного алгебраического свойства смешанного произведения).

18. Указание. 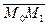(x1 - x0, y1 - y0, z1 - z0) и (x₃y₃z₃) неколлинеарны.

В качестве нормального вектора к плоскости можно взять 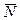= [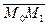,]. Или можно иначе: использовать условие компланарности трех векторов , , .

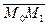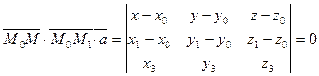
19. Указание. В качестве направляющего вектора можно взять 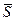= [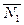,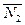], точку М найти из системы.

22.

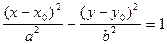
23, y - 18 = 0

24. a) k = tg j б) r = P/cos(j - a)

указание

25. Использовать нормальное уравнение прямой x cos a + y cos b - P = 0.

Учитывать, что cos b = sin a.

Литература

1. Беклеминов Д.В. Курс аналитической геометрии и линейной алгебры. - М.: Наука, 1990.

2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. - М.: Наука, 1990.

3. Клетеник Д.В. сборник задач по аналитической геометрии. - М.: Наука, 1975.