рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Доклады по дисциплине Дополнительные главы математической статистики . Регрессионный анализ. 4
Реферат Курсовая Конспект
Доклады по дисциплине Дополнительные главы математической статистики . Регрессионный анализ. 4
Доклады по дисциплине Дополнительные главы математической статистики . Регрессионный анализ. 4 - раздел Математика, Доклады По Дисциплине «Дополнительные Главы Математической Статистики». ...
Доклады по дисциплине «Дополнительные главы математической статистики».
Содержание
Регрессионный анализ. 4
§1.Теоретическая часть работы.. 4
1.1. Введение. 4
1.2. Виды регрессионного анализа. 5
1.3. Линейная регрессия. 7
§2. Практическая часть работы.. 12
2.1. Исследование линейной зависимости между ЧСС и мощностью выполняемой работы на основе РА.. 12
2.2. Исследование посещаемости WEB сайта на основе РА.. 15
Список литературы: 20
Нелинейное оценивание. 21
§1.Общее назначение. 21
§2.Оценивание линейных и нелинейных моделей. 24
§3.Основные типы нелинейных моделей. 25
3.1.Регрессионные модели с линейной структурой. 25
3.2.Существенно нелинейные регрессионные модели. 26
§4.Методы нелинейного оценивания . 31
4.1.Метод наименьших квадратов. 32
4.2.Функция потерь. 32
4.3.Метод взвешенных наименьших квадратов. 34
4.4.Метод максимума правдоподобия. 34
4.5.Максимум правдоподобия и пробит/логит модели. 35
4.6.Алгоритмы минимизации функций. 36
4.7.Начальные значения, размеры шагов и критерии сходимости. 37
4.9.Локальные минимумы. 38
4.10.Квази-ньютоновский метод. 38
4.11.Симплекс-метод. 38
4.13.Метод Розенброка. 39
4.14.Матрица Гессе и стандартные ошибки. 39
§5.Оценивание пригодности модели. 40
Список литературы: 40
Анализ функций распределения. 41
§1. Функция распределения вероятностей случайной величины и её характеристики 41
§2. Анализ функций распределения. 49
2.1. Распределения Пирсона (хи – квадрат), Стьюдента и Фишера. 49
2.2.Распределения Вейбулла - Гнеденко. 56
2.3. Распределение Рэлея. 60
Список литературы: 64
Факторный анализ. 66
§1.Основные понятия и определения. Примеры.. 66
§2.Методы факторного анализа. 73
2.1 Общий обзор методов факторного анализа. 73
2.2 Метод главных компонент. 75
2.3. Центроидный метод. 82
2.4 Метод экстремальной группировки параметров. 83
§3. Критерии рационального выбора числа факторов. 85
§4.. Общие выводы.. 87
Список литературы: 89
Подгонка функций распределения. 90
§1. Проверка качественных характеристик выборки. 90
1.1. Критерий Смирнова. 91
1.2. Критерий однородности Лемана-Розенблатта. 99
1.3. Метод минимального расстояния. 102
§2. Проверка количественных характеристик выборки. 104
Список литературы: 109
Кластерный анализ. 111
§1. Сущность, типологизация и прикладная направленность задач классификации объектов. 111
§2. Методы кластерного анализа. 119
2.1. Иерархические методы кластерного анализа. 119
2.2. Итеративные методы. 126
§3. Сравнительный анализ иерархических и неиерархических методов кластеризации. 129
§4. Новые алгоритмы и некоторые модификации алгоритмов кластерного анализа. 130
Дисперсионный анализ. 134
Введение. 135
§1. Дисперсионный анализ. 136
1.1 Основные понятия дисперсионного анализа. 136
1.2 Однофакторный дисперсионный анализ. 139
1.3 Многофакторный дисперсионный анализ. 147
§2.Применение дисперсионного анализа в различных процессах и исследованиях. 1
2.1 Использование дисперсионного анализа при изучении миграционных процессов. 1
2.2. Принципы математико-статистического анализа данных медико-биологических исследований. 1
2.3. Биотестирование почвы. 2
2.4.Дисперсионный анализ в химии. 3
Список используемых источников. 4
Регрессионный анализ
Теоретическая часть работы
Введение
«Регрессионный анализ (далее РА) – это основной метод современной математической статистики…» - так оценили роль РА отечественные ведущие специалисты в области прикладной математической статистики Ю.Адлер и В. Горский.
Несколько слов истории. На рубеже 18го и 19го (1803г. и 1805г.) столетия математики К.Гаусс и А.Лежандр независимо друг от друга заложили основы метода наименьших квадратов (МНК), ставшего в последствии базой линейного РА. Астрономия, геодезия и позже химия были первыми отраслями наук, где применялся МНК.
Первоначально термин «регрессия» был употреблен английским статистиком Ф.Гальтоном (1886) в связи с вопросом о наследственности роста. Гальтон нашел, что сыновья отцов, отклоняющихся по росту на x дюймов от среднего роста всех отцов, сами отклоняются от среднего роста всех сыновей меньше чем на x дюймов, то есть здесь на лицо то, что Гальтон назвал «регрессией к среднему состоянию» («regression to mediocrity»).
Классический РА включает:
· МНК;
· проверку гипотез об адекватности модели объекту;
· проверку гипотез о значимости оцененных коэффициентов выбранной модели.
С 20-х годов 20-го столетия РА стал использоваться в эконометрии, психологии, педагогике, социологии и медицине. С 50-х годов в связи с созданием ЭВМ начался «регрессионный бум».
Базисными постулатами классического РА являются:
· регрессия является линейной комбинацией с неизвестными коэффициентами линейной независимых функций от факторов;
· факторы – детерминированы;
· параметры – детерминированы;
· зависимые переменные (отклики) – некоррелированные, равноточные (с одинаковой дисперсией ошибок измерений) и распределены нормально;
· все переменные измеряются в непрерывных шкалах.
Большое разнообразие реальных ситуаций служило стимулом эволюции РА, развитию метода в направлении снятия классических ограничений и распространению его принципов на новые явления и процессы.
Виды регрессионного анализа
Последовательный регрессионный анализ (ПРА) - раздел МС, характерной чертой которого является то, что число производимых наблюдений (момент… Текущий регрессионный анализ (ТРА) (стохастическая аппроксимация) - метод… Байесовский регрессионный анализ (БРА) - в случае случайного характера коэффициентов регрессии с известным…Линейная регрессия
Цель РА состоит в определении общего вида уравнения регрессии, построении оценок неизвестных параметров, входящих в уравнение регрессии и проверке… Е(У|х) =g(х,b) и D(У|х)=s2h2(x), где b обозначает совокупность неизвестных параметров, определяющих функцию g(х), а h(х) есть известная функция х (в…Практическая часть работы
Исследование линейной зависимости между ЧСС и мощностью выполняемой работы на основе РА
1. Рассчитать значение нормированного коэффициента корреляции по формуле:Исследование посещаемости WEB сайта на основе РА
Описание объекта
Факторы формирующие моделируемое явление
Полученные данные с помощью программы наблюдения за компьютерной сетью (Net Medic, Net lab) являются не совсем точными, но довольно близки к… Зависимый фактор: N- количество человек в день посетивших сайт.Для модели в абсолютных показателях
Независимые факторы:
P - Загруженность внутренней сети (чел/день)
S – Cкорость обмена данными в сети Кбит/сек
V – Кол-во вакансий на текущий день
B – Количество «Баннеров» – рекламных ссылок на исследуемый сайт.
Данные представлены в таблице 1.
Таблица 1
| № Объекта наблюдения | N Кол-во человек в день | P Загруженность внутренней сети (чел/ден) | S Скорость обмена данными в сети Кбит/сек | V Кол-во вакансий на текущий день. | B Кол-во баннеров |
Анализ матрицы коэффициентов парных корреляций
Таблица 2
| № фактора | N | P | S | V | B |
| N | 1.00 | -0.22 | -0.06 | 0.44 | 0.12 |
| P | -0.22 | 1.00 | 0.91 | 0.68 | 0.74 |
| S | -0.06 | 0.91 | 1.00 | 0.86 | 0.91 |
| V | 0.44 | 0.68 | 0.86 | 1.00 | 0.85 |
| B | 0.12 | 0.74 | 0.91 | 0.85 | 1.00 |
Из таблицы 2 находим тесно коррелирующие факторы. Налицо мультиколлениарность факторов P и S ( 0.91 ). Оставим только один фактор P . И действительно если скорость в сети высокая то она может без значительных задержек во времени обработать значительное кол-во запросов от пользователей, значит чем больше скорость в сети тем больше в ней пользователей. Тем загруженее сеть.
Построение уравнения регрессии
Используя программное обеспечение «ОЛИМП» (которое в свою очередь использует для расчетов указанные выше принципы и формулы чем значительно… Путем перебора возможных комбинаций оставшихся факторных признаков получим… Функция N = +12.567-0.005*P+0.018*VСмысл модели
При увеличении загруженности внутренней сети в которой расположен сервер содержащий исследуемый сайт количество людей посетивших сайт будет…Список литературы
1. Ю. Адлер, В. Горский, Предисловие к русскому изданию 1/ Н. Дрейпер и Г. Смит, Прикладной регрессионный анализ. Кн.1. - М.: Финансы и статистика, 1986г.
2. Юл Дж. Э., Кендэл М. Дж Теория статистики, пер. с англ., 14 изд., М., 1960г.
З. Смирнов Н. И, Дунин-Барковский И. В, Курс теории вероятностей и математической статистики для технических приложений, З изд., М., 1969г.
4. Айвазян С. А., Статистическое исследование зависимостей, М., 1968; Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М.,
1968г.
5. «Теория статистики», учебник под редакцией проф. Р.А.Шмойловой, издательство «Финансы и статистика» 1996 г.Нелинейное оценивание
Общее назначение
а) стохастичны по своей природе, т. е. позволяют устанавливать лишь вероятностные логические соотношения между изучаемыми событиями А и В, а именно… б) выявляются на основании статистического наблюдения за анализируемыми… то мы оказываемся в рамках проблемы статистического исследования зависимостей. Соответствующий математический…Оценивание линейных и нелинейных моделей
y = F(x1, x2, ... , xn) При проведении регрессионного, а в частности нелинейного регрессионного… Примером модели такого типа может быть модель множественной линейной регрессии. В этой модели предполагается, что…Основные типы нелинейных моделей
· Регрессионные модели с линейной структурой
· Существенно нелинейные регрессионные модели
Регрессионные модели с линейной структурой
Производительность = a + b1*Возбуждение + b2*Возбуждение2 В этом уравнении a представляет свободный член, а b1 и b2 коэффициенты… Модели, нелинейные по параметрам. Для сравнения с предыдущим примером рассмотрим зависимость между возрастом человека…Существенно нелинейные регрессионные модели
Рост = exp(-b1*Возраст) + ошибка Аддитивная ошибка. В этой модели предполагается, что случайная ошибка не… Мультипликативная ошибка. В “оправдание” предыдущего примера заметим, что в данном случае постоянство вариации…Регрессионные модели с точками разрыва
y = b0 + b1*x*(x 500) + b2*x*(x > 500) В этой формуле: y означает оцениваемую себестоимость, а x равен объему… Вместо явного задания точки разрыва регрессионной кривой (500 единиц в месяц в последнем примере), можно также оценить…Методы нелинейного оценивания
4.1.Метод наименьших квадратов. После выбора модели возникает вопрос: каким образом можно оценить эти модели?… Определим модель в виде и рассмотрим способ оценки параметра в зависимости от предположений о природе Х и характере…Начальные значения, размеры шагов и критерии сходимости.
4.8.Штрафные функции, ограничение параметров. Все процедуры Нелинейного оценивания не имеют встроенных ограничений на… Для того, чтобы определить ограничения на область изменения параметров, следует добавить к функции потерь некоторую…Оценивание пригодности модели
Список литературы
1. Айвазян С.А. и др. Прикладная статистика: Исследование зависимостей. Под ред. С.А.Айвазяна. - М.: Финансы и статистика, 1985.
2. Айвазян С.А. и др. Классификация многомерных наблюдений. - М.: Статистика, 1974.
3. Андерсон Т. Введение в многомерный статистический анализ. Пер. с англ. – М.: Физматгиз, 1963.
4. Ван-дер-Варден Б. Л. Математическая статистика. Пер. с нем. – М.: ИЛ, 1960.
5. Кендалл М. Дж., Стьюарт А. Теория распределений. Пер. с англ. – М.: Наука,1966.
6. Крамер Г. Математические методы статистики. – 2-е изд. Пер. с англ. – М.: Мир, 1975.
7. Шеффе Г. Дисперсионный анализ. Пер. с англ. – М.: Физматгиз, 1963.
Анализ функций распределения
Функция распределения вероятностей случайной величины и её характеристики
Одномерной случайной величиной  , или просто случайной величиной, называют любую числовую функцию, определенную на пространстве элементарных событий
, или просто случайной величиной, называют любую числовую функцию, определенную на пространстве элементарных событий 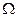 .
.
Пример.
Рассмотрим пространство элементарных событий, которое получается в результате независимых бросаний двух монет. В этом примере пространство элементарных событий состоит из четырех элементарных событий, которым сопоставляется вероятность 1/4. Определим теперь на этом пространстве случайную величину  , равную числу гербов, появившихся при бросании двух монет. Очевидно, что значения случайной величины
, равную числу гербов, появившихся при бросании двух монет. Очевидно, что значения случайной величины  есть 0, 1, 2, и случайная величина принимает эти значения с вероятностями 0,25, 0,5, 0,25, соответственно.
есть 0, 1, 2, и случайная величина принимает эти значения с вероятностями 0,25, 0,5, 0,25, соответственно.
Так как одномерная случайная величина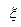 представляет собой числовую функцию на пространстве элементарных событий, то любая числовая функция
представляет собой числовую функцию на пространстве элементарных событий, то любая числовая функция 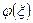 от случайной величины в соответствии с определением также является случайной величиной.
от случайной величины в соответствии с определением также является случайной величиной.
Определение 1.1. Функцией распределения вероятностей, или просто функцией распределения (иногда применяют термин кумулятивная функция распределения) случайной величины  , называется функция
, называется функция  , равная для любого значения
, равная для любого значения  вероятности события
вероятности события 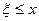 :
:
 (1.1)
(1.1)
Иногда в литературе применяется другое обозначение функции распределения вероятностей случайной величины 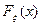 .
.
Из определения (1.1) легко вывести свойства функции распределения:
1. 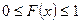
2.  - неубывающая функция
- неубывающая функция
3. 
4. 
5. 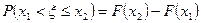 .
.
Графическое изображение функции распределения представляет собой неубывающую кривую, значения которой лежат в интервале от 0 до 1 (рис.1.1, рис.1.2).
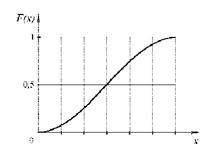
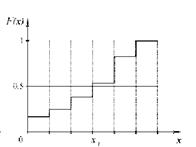
Рис.1.1. Распределение непрерывной Рис.1.2. Распределение дискретной
случайной величины случайной величины
На рис. 1.3 приведен график функции распределения вероятностей случайной величины из примера, рассмотренного ранее.

Рис. 1.3. Функция распределения F(x) случайной величины.
Важнейшими среди характеристик распределений являются математическое ожидание, дисперсия, среднее квадратическое отклонение, коэффициент вариации, моменты, центральные моменты, коэффициент асимметрии, коэффициент эксцесса, медиана, мода, первая квартиль, третья квартиль, интерквартильный размах, квантили.
Определение 1.2. Математическим ожиданием случайной величины  (иногда применяется термин среднее или генеральное среднее) называется число
(иногда применяется термин среднее или генеральное среднее) называется число 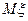 (другие распространенные обозначения:
(другие распространенные обозначения:  ), равное
), равное
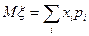 , если
, если  - дискретная случайная величина и
- дискретная случайная величина и
 , если
, если  - непрерывная случайная величина.
- непрерывная случайная величина.
Математическое ожидание 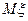 является характеристикой положения центра распределения, или, как иногда говорят, мерой центральной тенденции, или средним по вероятностям случайной величины.
является характеристикой положения центра распределения, или, как иногда говорят, мерой центральной тенденции, или средним по вероятностям случайной величины.
Свойства математического ожидания:
1. 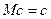 , где
, где 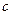 - константа
- константа
2. 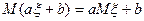 , где
, где  и
и  - константы
- константы
3. Для любых двух случайных величин  и
и 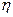 :
: 
4. Если  и
и 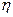 - независимые случайные величины, то
- независимые случайные величины, то 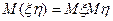
 5. Если
5. Если  - некоторая функция, то (при довольно общих ограничениях)
- некоторая функция, то (при довольно общих ограничениях) 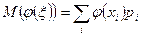 для дискретной случайной величины
для дискретной случайной величины  и
и  для непрерывной случайной величины
для непрерывной случайной величины  .
.
Для описания многих практически важных свойств случайной величины необходимо знание не только ее математического ожидания, но и отклонения возможных ее значений от среднего значения.
Для измерения разброса значений случайной величины около среднего значения часто используют такие характеристики как дисперсия, среднее квадратическое отклонение, коэффициент вариации.
Определение 1.3. Дисперсией случайной величины называется число  (другие распространенные обозначения:
(другие распространенные обозначения: 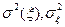 ), равное
), равное
 если
если  - дискретная случайная величина, и
- дискретная случайная величина, и 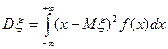 если
если  - непрерывная случайная величина.
- непрерывная случайная величина.
Дисперсия характеризует средний квадрат отклонения случайной величины от своего математического ожидания.
Свойства дисперсии:
1. 
2. 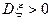
3. 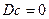 , где
, где 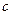 - константа
- константа
4.  , где
, где  и
и  - константы
- константы
5. Если  и
и 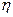 - независимые случайные величины, то
- независимые случайные величины, то 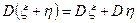
Из свойств  следует, что
следует, что 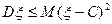 , причем равенство имеет место только при
, причем равенство имеет место только при 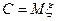 . Т.е.
. Т.е. 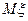 минимизирует средний квадрат отклонения
минимизирует средний квадрат отклонения  .
.
Определение 1.4. Средним квадратическим отклонением случайной величины (иногда применяется термин «стандартное отклонение случайной величины») называется число , равное
, равное 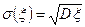 .
.
Среднее квадратическое отклонение, следовательно, является, как и дисперсия, мерой рассеяния распределения, но измеряется, в отличие от дисперсии, в тех же единицах, которые используют для измерения значений случайной величины.
Определение 1.5. Коэффициентом вариации случайной величины  называется число
называется число  , равное, если
, равное, если ,
,  .
.
Таким образом, коэффициент вариации является, как и дисперсия, и среднее квадратическое отклонение, мерой рассеяния распределения, но служит для измерения среднего квадратического отклонения в долях математического ожидания.
Определение 1.6. Моментом порядка  (иногда применяют термин «начальный момент порядка
(иногда применяют термин «начальный момент порядка  ») случайной величины называется число
») случайной величины называется число , равное
, равное  .
.
Определение 1.7 Центральным моментом порядка  случайной величины
случайной величины  называется число
называется число 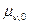 , равное
, равное  .
.
Таким образом, математическое ожидание случайной величины есть момент первого порядка, а дисперсия - центральный момент второго порядка.
Кроме этих моментов наиболее часто используется третий и четвертый центральные моменты.
Определение 1.8. Коэффициентом асимметрии («скошенности») случайной величины  называется величина
называется величина  , а коэффициентом эксцесса («островершинности») случайной величины
, а коэффициентом эксцесса («островершинности») случайной величины  - величина
- величина 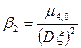 .
.

Рис. 1.4. Пример распределений с положительной (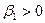 ) и отрицательной (
) и отрицательной ( ) асимметрией.
) асимметрией.
Если плотность распределения случайной величины симметрична, то коэффициент асимметрии . На рис. 1.4 приведены графики функций плотности в двух случаях:
. На рис. 1.4 приведены графики функций плотности в двух случаях: 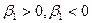 . Для нормального распределения коэффициент эксцесса
. Для нормального распределения коэффициент эксцесса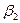 равен 3. Если же распределение сосредоточено вокруг среднего теснее, чем нормальное, то
равен 3. Если же распределение сосредоточено вокруг среднего теснее, чем нормальное, то 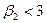 , в противном случае
, в противном случае  .
.
Другими характеристиками положения являются медиана и мода.
Определение 1.9. Медианой случайной величины  называется такое число
называется такое число  , что
, что  ,
, 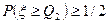 .
.
Если  - непрерывная случайная величина, то определение медианы полезно интерпретировать через функцию плотности, как это показано на рис. 1.5. Таким образом, для непрерывной случайной величины
- непрерывная случайная величина, то определение медианы полезно интерпретировать через функцию плотности, как это показано на рис. 1.5. Таким образом, для непрерывной случайной величины  .
.
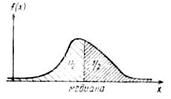
Рис. 1.5. Медиана распределения
Если распределение случайной величины симметрично, как, например, в случае нормального распределения, то медиана совпадает с математическим ожиданием. Иногда математическому ожиданию приписывается смысл медианы, что, конечно же, неверно, так как математическое ожидание и медиана для несимметричных распределений, вообще говоря, не совпадают.
Определение 1.10. Модой непрерывной случайной величины называется такое значение  , в котором
, в котором  достигает своего локального максимума.
достигает своего локального максимума.
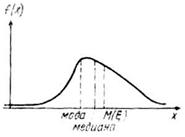
Рис. 1.6. Мода, медиана и математическое ожидание.
Мода есть «центр сгущения» случайной величины в смысле наиболее часто встречающихся значений случайной величины. Распределение с одной модой называется унимодальным, а распределение с несколькими модами - мультимодальным. Для симметричного унимодального распределения мода совпадает с математическим ожиданием, а, следовательно, и с медианой. Как в случае с медианой, иногда математическому ожиданию приписывают смысл моды, что, конечно же, неверно, так как математическое ожидание и мода для несимметричных распределений не совпадают.
На рис. 1.6 для несимметричного унимодального распределения показаны все три характеристики положения распределения.
Можно ввести еще две характеристики распределения, аналогичные медиане: первую квартиль и третью квартиль.
Определение 1.11. Первой квартилью распределения случайной величины  называется такое число
называется такое число 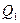 что
что 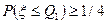 ,
, 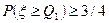 , а третьей квартилью распределения случайной величины
, а третьей квартилью распределения случайной величины  называется такое число
называется такое число 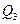 , что
, что 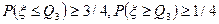 .
.
Если  - непрерывная случайная величина, то это определение квартили полезно интерпретировать через функцию плотности в соответствии с рис. 1.7.
- непрерывная случайная величина, то это определение квартили полезно интерпретировать через функцию плотности в соответствии с рис. 1.7.

Рис. 1.7. Первая и третья квартили распределения.
Таким образом, для непрерывной случайной величины 
 и
и 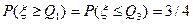 .
.
Следовательно, вероятность того, что случайная величина примет значение в интервале 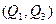 , равна
, равна 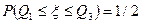 .
.
Заметим, что длина этого интервала  называется интерквартильным размахом и может служить, аналогично среднеквадратическому отклонению, мерой рассеяния значений случайной величины.
называется интерквартильным размахом и может служить, аналогично среднеквадратическому отклонению, мерой рассеяния значений случайной величины.
Определение 1.12. Квантилью порядка 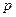 распределения
распределения  называется число
называется число 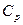 , такое, что
, такое, что 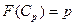 .
.
Для непрерывной случайной величины это определение полезно интерпретировать через функцию плотности, как показано на рис. 1.8.

Рис. 1.8. Графическая иллюстрация определения квантили.
Из определения квантили следует, что медиана есть квантиль порядка 0.5, первая квартиль - квантиль порядка 0.25, а третья квартиль - квантиль порядка 0.75.
Для некоторых, наиболее распространенных в математической статистике распределений созданы таблицы квантилей.
Очень часто, особенно в пакетах прикладных программ по статистической обработке, вместо термина «квантиль» используется термин «процентиль», когда порядок квантили выражается в процентах.

§2. Анализ функций распределения
Распределения Пирсона (хи – квадрат), Стьюдента и Фишера.
Распределение Пирсона (хи - квадрат) – распределение случайной величины , где случайные величины независимы и имеют одно и тоже распределение . При… Распределение хи-квадрат используют при оценивании дисперсии (с помощью…Пример распределения хи-квадрат
Пусть фирма выпустила новый процессор. Предположим, что каждые два года цена на этот процессор падает на 10%. Тогда количество таких процессоров, которые можно купить на фиксированную сумму может быть описано с помощью распределения хи-квадрат.
Доказательство:
Обозначим фиксированную сумму через Z. Пусть S - стартовая цена процессора. Тогда по прошествии 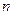 лет он будет стоить
лет он будет стоить  . Преобразуем полученное выражение:
. Преобразуем полученное выражение: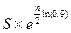 . Введем новую переменную:
. Введем новую переменную: 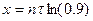 . Получим следующую формулу:
. Получим следующую формулу: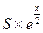 . Количество процессоров, которые можно купить на фиксированную сумму, равно
. Количество процессоров, которые можно купить на фиксированную сумму, равно  . Если закрыть глаза на коэффициенты, то полученная формула соответствует формуле плотности для распределения хи-квадрат при
. Если закрыть глаза на коэффициенты, то полученная формула соответствует формуле плотности для распределения хи-квадрат при 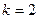 .
.
Распределение 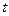 Стьюдента – это распределение случайной величины
Стьюдента – это распределение случайной величины  ,
,
где случайные величины 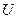 и
и 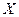 независимы,
независимы, 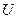 имеет стандартное нормальное распределение
имеет стандартное нормальное распределение  , а
, а 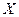 – распределение хи – квадрат с
– распределение хи – квадрат с 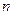 степенями свободы. При этом
степенями свободы. При этом 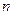 называется «числом степеней свободы» распределения Стьюдента.
называется «числом степеней свободы» распределения Стьюдента.
Распределение Стьюдента было введено в 1908 г. английским статистиком В.Госсетом, работавшем на фабрике, выпускающей пиво. Вероятностно-статистические методы использовались для принятия экономических и технических решений на этой фабрике, поэтому ее руководство запрещало В.Госсету публиковать научные статьи под своим именем. Таким способом охранялась коммерческая тайна, «ноу-хау» в виде вероятностно-статистических методов, разработанных В.Госсетом. Однако он имел возможность публиковаться под псевдонимом «Стьюдент». История Госсета - Стьюдента показывает, что еще сто лет назад менеджерам Великобритании была очевидна большая экономическая эффективность вероятностно-статистических методов.
В настоящее время распределение Стьюдента – одно из наиболее известных распределений среди используемых при анализе реальных данных. Его применяют при оценивании математического ожидания, прогнозного значения и других характеристик с помощью доверительных интервалов, по проверке гипотез о значениях математических ожиданий, коэффициентов регрессионной зависимости, гипотез однородности выборок и т.д.
В теории вероятностей дается следующее конструктивное определение распределения Стьюдента.
Предположим, что каждая из 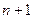 независимых случайных величин
независимых случайных величин 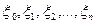 , распределена нормально с параметрами
, распределена нормально с параметрами 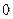 и
и 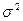 (
( ). Тогда случайная величина
). Тогда случайная величина 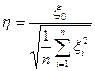 имеет распределение Стьюдента с
имеет распределение Стьюдента с 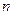 степенями свободы (записывается
степенями свободы (записывается  ).
).
График функции плотности 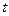 -распределения см. на рис. 2.1.2 в двух вариантах:
-распределения см. на рис. 2.1.2 в двух вариантах: 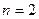 и
и  . Заметим, что максимальное значение плотности распределения достигается при
. Заметим, что максимальное значение плотности распределения достигается при 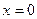 , и график симметричен относительно оси ординат.
, и график симметричен относительно оси ординат.

Рис. 2.1.2. Функция плотности 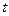 -распределения в двух вариантах: (1)
-распределения в двух вариантах: (1)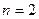 , (2)
, (2)  .
.
Основные характеристики распределения Стьюдента
| Обозначение | 
|
| Область значений | 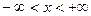
|
| Параметры | Параметр формы 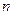 , число степеней свободы, целое положительное число , число степеней свободы, целое положительное число
|
| Плотность (функция вероятности) | 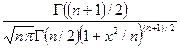
|
| Математическое ожидание | 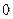
|
| Дисперсия |  , если , если 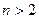
|
| Функция распределения | Не выражается в элементарных функциях |
| Медиана | 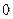
|
| Мода | 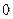
|
| Коэффициент асимметрии | 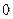 , если , если 
|
| Коэффициент эксцесса | 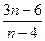 , где , где 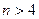
|
Свойства распределения.
1. Распределение Стьюдента симметрично. В частности, если  , то
, то 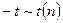 .
.
2. Случайная величина  имеет только моменты порядков
имеет только моменты порядков 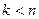 , причем
, причем  , если
, если  - нечетно;
- нечетно;  , если
, если  - четно. Моменты порядков
- четно. Моменты порядков 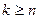 не определены.
не определены.
Связь с другими распределениями:
1. Распределение Стьюдента сходится к стандартному нормальному при 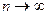 . Пусть дана последовательность случайных величин
. Пусть дана последовательность случайных величин  , где
, где 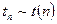 ,
, 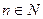 . Тогда
. Тогда 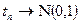
 по распределению при
по распределению при 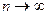 .
.
2. Квадрат случайной величины, имеющей распределение Стьюдента, имеет распределение Фишера. Пусть  , тогда
, тогда 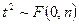 .
.

Пример распределения Стьюдента
Пусть имеется устройство вывода, для которого можно установить режим 
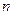 пикселей, где
пикселей, где 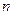 - целое положительное число. Предположим, что оно получает информацию сразу по всей выходной матрице, а затем выводит ее по точкам. Тогда скорость обработки изображения будет подчиняться распределению Стьюдента.
- целое положительное число. Предположим, что оно получает информацию сразу по всей выходной матрице, а затем выводит ее по точкам. Тогда скорость обработки изображения будет подчиняться распределению Стьюдента.
Доказательство:
Так как вывод производится по точкам, то потребуется вывести точку ровно 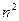 раз. Кроме того, потребуется также один раз принять информацию. В итоге получим, что требуется
раз. Кроме того, потребуется также один раз принять информацию. В итоге получим, что требуется  единиц времени. Скорость обработки обратно пропорциональна затраченному времени, т. е. . Если пренебречь коэффициентами, то последняя
единиц времени. Скорость обработки обратно пропорциональна затраченному времени, т. е. . Если пренебречь коэффициентами, то последняя 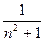 формула соответствует формуле для плотности распределения Стьюдента при
формула соответствует формуле для плотности распределения Стьюдента при 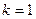 .
.
Распределение Фишера – это распределение случайной величины  ,
,
где случайные величины  и
и  независимы и имеют распределения хи – квадрат с числом степеней свободы
независимы и имеют распределения хи – квадрат с числом степеней свободы 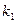 и
и  соответственно. При этом пара (
соответственно. При этом пара (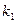 ,
, ) – пара «чисел степеней свободы» распределения Фишера, а именно,
) – пара «чисел степеней свободы» распределения Фишера, а именно, 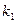 – число степеней свободы числителя, а
– число степеней свободы числителя, а  – число степеней свободы знаменателя. Распределение случайной величины
– число степеней свободы знаменателя. Распределение случайной величины 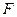 названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики .
Предположим теперь, что каждая из  независимых случайных величин
независимых случайных величин 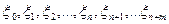 распределена нормально с параметрами
распределена нормально с параметрами 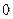 и
и 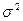 (
( ). Тогда случайная величина
). Тогда случайная величина 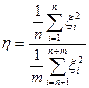 имеет F-распределение с
имеет F-распределение с 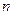 и
и 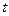 степенями свободы (записывается
степенями свободы (записывается  ).
).
График функции плотности 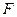 -распределения представлен на рис. 2.1.3 в двух вариантах:
-распределения представлен на рис. 2.1.3 в двух вариантах:  и
и  .
.
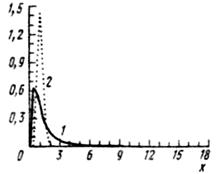
Рис. 2.1.3. Функция плотности 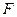 -распределения: (1)
-распределения: (1)  ; (2)
; (2)  .
.
Основные характеристики распределения Фишера
| Обозначение | 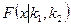
|
| Область значений | 
|
| Параметры | Количества степеней свободы – целые положительные числа 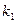 и и  , параметры формы. , параметры формы.
|
| Плотность |  
|
| Математическое ожидание | 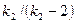 , , 
|
| Дисперсия | 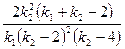 , , 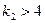
|
| Функция распределения | Не выражается в элементарных функциях |
| Мода | 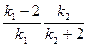 , если , если 
|
| Коэффициент асимметрии | 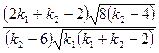 , если , если 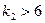
|
Свойства распределения:
1. Если  , то
, то 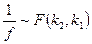
 .
.
2. Распределение Фишера сходится к единице, если  , то
, то  по распределению при
по распределению при 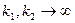 , где
, где  -дельта-функция в единице, т.е. распределение случайной величины-константы
-дельта-функция в единице, т.е. распределение случайной величины-константы 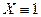 .
.

Связь с другими распределениями:
1. Если  , то случайные величины
, то случайные величины 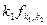 сходятся по распределению к
сходятся по распределению к 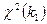 при
при 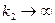 .
.
Распределения Вейбулла - Гнеденко
(2.2.1) где и - функция распределения и плотность случайной величины. Опишем типичное поведение интенсивности отказа. Весь интервал времени можно разбить на три периода. На первом из них…Пример распределения Вейбулла
Известно, что "период полураспада" знаний о компьютерных технологиях составляет 2 года. Это значит, что каждые два года половина наших знаний безнадежно устаревает. Коэффициент изменения остаточных полезных знаний по прошествии  лет подчиняется распределению Вейбулла.
лет подчиняется распределению Вейбулла.
Доказательство:
Предположим, что A - первоначальное количество полезной информации. Тогда через 2 года количество полезной информации станет равным 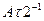 , а по прошествии
, а по прошествии  лет примет вид
лет примет вид  . Коэффициент изменения остаточных полезных знаний равен
. Коэффициент изменения остаточных полезных знаний равен  . Введем новую переменную
. Введем новую переменную 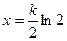 . Коэффициент изменения остаточных полезных знаний примет следующий вид:
. Коэффициент изменения остаточных полезных знаний примет следующий вид: 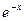 . Итоговая формула совпадает с формулой плотности вероятности для распределения Вейбулла при
. Итоговая формула совпадает с формулой плотности вероятности для распределения Вейбулла при  . прошествии
. прошествии  лет подчиняется распределению Вейбулла.
лет подчиняется распределению Вейбулла.
Распределение Рэлея
Распределение является геометрической суммой случайных величин , подчиненных закону Гаусса с параметрами : . Плотность вероятности распределения Рэлея имеет вид: (2.3.1)Пример
На сновальной машине в результате погрешности крепления в пинолях сновального вала его намотка имеет эксцентриситет. Экспериментально получено, что и минимальный радиус намотки при вращении вала изменяется случайно со средним квадратическим отклонением  =0,5 мм.
=0,5 мм.
Нормированное распределение Рэлея  не зависит от параметра
не зависит от параметра  , изменение
, изменение  показано на рис. 2.3.1(а), а величины
показано на рис. 2.3.1(а), а величины  и
и  для данного эксперимента
для данного эксперимента  =1,25;
=1,25;  =0,63 мм;
=0,63 мм;  =0,655;
=0,655;  =0,33 мм.
=0,33 мм.
Список литературы
1. Орлов А.И. Математика случая. Вероятность и статистика – основные факты. - Учебное пособие. М.: МЗ-Пресс, 2004.
2. http://www.aup.ru/books/m155/
3. Смирнов Н.В., Дунин - Барковский И.В. Курс теории вероятностей и математической статистики для технических приложений. М.: Наука, 1965. 511с.
4. Элементы математической статистики/ О.И. Тескин, Н.Е. Козлов, Г.М. Цветкова, Е.М. Пашовкин. М.: Изд-во МГТУ, 1995. 107 с.
5. Бочаров А.А.Теория вероятностей. Математическая статистика. М.: Гардарика, 1998. 328.
6. Ивченко Г.И., Медведев Ю.И. Математическая статистика. М.: Высш.шк., 1992. 304.
7. Письменный Д. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. М.: Айрис-пресс,2006. 288с.
Факторный анализ
Основные понятия и определения. Примеры
Основы ФА зародились в конце 19 века, когда Ф. Гальтон и К. Пирсон, работая с антропометрическими и психологическими данными, начали развивать идею латентных, генерализованных признаков. В 1901 г. К.Пирсон выдвинул эту идею, назвав его методом главных осей (компонент). Началом современного периода развития факторного анализа считают публикацию Ч. Спирмена « General intelligence objectively determined and measured» от 1904 г.
Факторный анализ - метод многомерного статистического анализа, позволяющий на основе экспериментального наблюдения признаков объекта выделить группу переменных, определяющих корреляционную взаимосвязь между признаками. Например, при проведении элементного анализа предельных углеводородов можно отдельно измерять массовую долю углерода и массовую долю водорода - два признака. Однако, эти признаки не являются независимыми (коррелируют между собой) и оба определяются длиной углеродной цепи. В этом и состоит суть факторного анализа - на основе исследования корреляционных взаимосвязей признаков находить причины, определяющие эти взаимосвязи
Неявность характеристик, раскрываемых при помощи методов факторного анализа, является ключевой . Вначале мы имеем дело с набором элементарных признаков Xj их взаимодействие предполагает наличие определенных причин, особенных условий, т.е. существование некоторых скрытых факторов. Последние устанавливаются в результате обобщения элементарных признаков и выступают как интегрированные характеристики, или признаки, но более высокого уровня. Естественно, что коррелировать могут не только тривиальные признаки Xj но и сами наблюдаемые объекты Ni. поэтому поиск латентных , то есть неявных, факторов теоретически возможен как по признаковым, так и по объектным данным.
Модели с латентными переменными применяются при решении следующих задач:
- понижение размерности признакового пространства,
- классификация объектов на основе сжатого признакового пространства,
- косвенной оценки признаков, не поддающихся непосредственному измерению,
- преобразование исходных переменных к более удобному для интерпретации виду.
Рассмотрим несколько примеров
 |
Предположим, n наблюдаемых объектов (автомобилей) оценивается в двумерном признаковом пространстве R2 с координатными осями: Х1 - стоимость автомобиля и Х2 - длительность рабочего ресурса мотора. При условии коррелированности Х1 и Х2 в системе координат появляется направленное и достаточно плотное скопление точек, формально отображаемое новыми осями (F1 и F2). Характерная особенность F1 и F2 заключается в том, что они проходят через плотные скопления точек и в свою очередь коррелируют с Х1 и Х2. Максимальное число новых осей Fr будет равно числу элементарных признаков (рис. 1 а, б).
На рисунке 1 дано геометрическое представление n наблюдаемых объектов в тривиальном пространстве элементарных признаков (а) и латентных факторов (б).
Допуская линейную зависимость Fr от Xj можем записать:
F1=a1x1+a2x2 и F2=a3x1+a4x2
Интерпретируем оси Fr: пусть F1 - экономичность автомобиля, F2 - его надежность в эксплуатации. Суждение об F1 и F2 базируется на оценке структуры латентных факторов, т. е. оценке весов Х1 и Х2 в Fr а именно по значениям коэффициентов aj.
Если объекты характеризуются достаточно большим числом элементарных признаков ( т > 3 ), то логично и другое предположение - о существовании плотных скоплений точек (признаков) в пространстве n объектов. При этом новые оси обобщают уже не признаки Xj, а объекты ni, соответственно и латентные факторы Fr будут распознаны по составу наблюдаемых объектов:
Fr=c1n1+c2n2+…+cNnN ,
где ci- вес объекта ni в факторе Fr.
Гипотетически легко представить следствием такого анализа, скажем, выявление классифицирующих факторов: F1 - промышленность, F2 - сельское хозяйство и т. п.
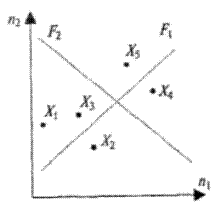 На рис. 2 приведён один из примеров распределения значений признаков (Х1 -стоимость автомобиля, Х2 - длительность рабочего ресурса мотора, Х3- время набора максимальной скорости после старта, Х4 - количество потребляемого бензина на 100 км пути, Х5 - дальность тормозного пути) в координатном пространстве для двух видов автомобилей: n1- «Вольво» и n2- «Фольксваген».
На рис. 2 приведён один из примеров распределения значений признаков (Х1 -стоимость автомобиля, Х2 - длительность рабочего ресурса мотора, Х3- время набора максимальной скорости после старта, Х4 - количество потребляемого бензина на 100 км пути, Х5 - дальность тормозного пути) в координатном пространстве для двух видов автомобилей: n1- «Вольво» и n2- «Фольксваген».
В зависимости от того, какой из рассмотренных выше тип корреляционной связи - элементарных признаков или наблюдаемых объектов исследуется в факторном анализе, различают R и Q - технические приемы обработки данных. Название R-техники носит объемный анализ данных по m признакам, в результате него получают r линейных комбинаций (групп) признаков (Fr=f(Xj);r =1..m).
Анализ по данным о близости (связи) n наблюдаемых объектов называется Q-техникой и позволяет определять r линейных комбинаций (групп) объектов: (F=f(ni);i =1..N).
В настоящее время на практике более 90% задач решается при помощи R-техники.
При использовании регрессионного анализа акцент делается на выявлении веса каждого факторного признака, воздействующего на результат, на количественную оценку чистого воздействия данного фактора при элиминировании остальных.
Существует и другой подход к исследованию структуры взаимодействия признаков, развивающийся в рамках факторного анализа. Этот подход основан на представлении о комплексном характере изучаемого явления, выражающемся, в частности, во взаимосвязях и взаимообусловленности отдельных признаков. Акцент в факторном анализе делается на исследовании внутренних причин, формирующих специфику изучаемого явления, на выявлении обобщенных факторов, которые стоят за соответствующими конкретными показателями.
Факторный анализ не требует априорного разделения признаков на зависимые и независимые, так как все признаки в нем рассматриваются как равноправные. Здесь нет допущения о неизменности всех прочих условий, свойственного регрессионно-корреляционному анализу.
Цель факторного анализа - сконцентрировать исходную информацию, выражая большое число рассматриваемых признаков через меньшее число более емких внутренних характеристик явления, которые, однако, не поддаются непосредственному измерению (например, уровень аграрного развития). При этом предполагается, что наиболее емкие характеристики окажутся одновременно и наиболее существенными, определяющими. В дальнейшем будем их называть обобщенными факторами (или просто факторами). Таким образом, главными целями факторного анализа являются: (1) сокращение числа переменных (редукция данных) и (2) определение структуры взаимосвязей между переменными, т.е. классификация переменных. Поэтому факторный анализ используется или как метод сокращения данных или как метод классификации.
Основной задачей, которую решают разнообразными методами факторного анализа, включая и метод главных компонент, является сжатие информации, переход от множества значений по m элементарным признакам с объемом информации (п * т) к ограниченному множеству элементов матрицы факторного
отображения (т * r) или матрицы значений неявных факторов для каждого наблюдаемого объекта размерностью (п *r ), причем обычно r < т.
Методы факторного анализа позволяют также визуализировать структуру изучаемых явлений и процессов, а это значит определить их состояние и спрогнозировать развитие. Наконец, данные факторного анализа дают основания для идентификации объекта, т.е. решения задачи распознавания образа.
Методы факторного анализа обладают свойствами, весьма привлекательными для их использования в составе других статистических методов, наиболее часто в корреляционно-регрессионном анализе, кластерном анализе, многомерном шкалировании и др.
Факторный анализ как метод редукции данных
Предположим, вы хотите измерить удовлетворенность людей жизнью, для чего составляете вопросник с различными пунктами; среди других вопросов задаете… Пусть имеется n объектов, каждый из которых характеризуется набором из m… Если все m признаков X1, ...,Xm - количественные, то матрицу данных можно обрабатывать с помощью методов факторного…Методы факторного анализа
Общий обзор методов факторного анализа
Набор методов факторного анализа в настоящее время достаточно велик, насчитывает десятки различных подходов и приемов обработки данных. Чтобы в… 1. Метод главных компонент (Г. Хотеллинг). Строго говоря, его не относят к… главные компоненты и их число первоначально равно числу элементарных признаков; во-вторых, постулируется возможность…Метод главных компонент
X1=a11F1+...+a1mFm .................................... (1) Xm=am1F1+...+ammFmФакторный анализ как метод классификации
Возвратимся к интерпретации результатов факторного анализа. Термин факторный анализ теперь будет включать как анализ главных компонент, так и анализ главных факторов. Предполагается, что вы находитесь в той точке анализа, когда в целом знаете, сколько факторов следует выделить. Вы можете захотеть узнать значимость факторов, то есть, можно ли интерпретировать их разумным образом и как это сделать. Чтобы проиллюстрировать, каким образом это может быть сделано, производятся действия "в обратном порядке", то есть, начинают с некоторой осмысленной структуры, а затем смотрят, как она отражается на результатах. Вернемся к примеру об удовлетворенности; ниже приведена корреляционная матрица для переменных, относящихся к удовлетворенности на работе и дома.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ | Корреляции (factor.sta) Построчное удаление ПД n=100 | |||||
| Переменная | РАБОТА_1 | РАБОТА_2 | РАБОТА_3 | ДОМ_1 | ДОМ_2 | ДОМ_3 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 | 1.00 .65 .65 .14 .15 .14 | .65 1.00 .73 .14 .18 .24 | .65 .73 1.00 .16 .24 .25 | .14 .14 .16 1.00 .66 .59 | .15 .18 .24 .66 1.00 .73 | .14 .24 .25 .59 .73 1.00 |
Переменные, относящиеся к удовлетворенности на работе, более коррелированы между собой, а переменные, относящиеся к удовлетворенности домом, также более коррелированы между собой. Корреляции между этими двумя типами переменных (переменные, связанные с удовлетворенностью на работе, и переменные, связанные с удовлетворенностью домом) сравнительно малы. Поэтому кажется правдоподобным, что имеются два относительно независимых фактора (два типа факторов), отраженных в корреляционной матрице: один относится к удовлетворенности на работе, а другой к удовлетворенности домашней жизнью.
Факторные нагрузки. Теперь проведем анализ главных компонент и рассмотрим решение с двумя факторами. Для этого рассмотрим корреляции между переменными и двумя факторами (или "новыми" переменными), как они были выделены по умолчанию; эти корреляции называются факторными нагрузками.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ | Факторные нагрузки (Нет вращения) Главные компоненты | |
| Переменная | Фактор 1 | Фактор 2 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 | .654384 .715256 .741688 .634120 .706267 .707446 | .564143 .541444 .508212 -.563123 -.572658 -.525602 |
| Общая дисперсия Доля общей дисп. | 2.891313 .481885 | 1.791000 .298500 |
По-видимому, первый фактор более коррелирует с переменными, чем второй. Это следовало ожидать, потому что, как было сказано выше, факторы выделяются последовательно и содержат все меньше и меньше общей дисперсии.
Вращение факторной структуры. Вы можете изобразить факторные нагрузки в виде диаграммы рассеяния. На этой диаграмме каждая переменная представлена точкой. Можно повернуть оси в любом направлении без изменения относительного положения точек; однако действительные координаты точек, то есть факторные нагрузки, должны, без сомнения, меняться. Если вы построите диаграмму для этого примера, то увидите, что если повернуть оси относительно начала координат на 45 градусов, то можно достичь ясного представления о нагрузках, определяющих переменные: удовлетворенность на работе и дома.
Методы вращения. Существуют различные методы вращения факторов. Целью этих методов является получение понятной (интерпретируемой) матрицы нагрузок, то есть факторов, которые ясно отмечены высокими нагрузками для некоторых переменных и низкими - для других. Эту общую модель иногда называют простой структурой (более формальное определение можно найти в стандартных учебниках). Типичными методами вращения являются стратегии варимакс, квартимакс, и эквимакс.
Варимакс можно успешно применить и к рассматриваемой задаче. Как и ранее, вы хотите найти вращение, максимизирующее дисперсию по новым осям; другими словами, вы хотите получить матрицу нагрузок на каждый фактор таким образом, чтобы они отличались максимально возможным образом и имелась возможность их простой интерпретации. Ниже приведена таблица нагрузок на повернутые факторы.
| STATISTICA ФАКТОРНЫЙ АНАЛИЗ | Факторные нагрузки (Варимакс нормализ.) Выделение: Главные компоненты | |
| Переменная | Фактор 1 | Фактор 2 |
| РАБОТА_1 РАБОТА_2 РАБОТА_3 ДОМ_1 ДОМ_2 ДОМ_3 | .862443 .890267 .886055 .062145 .107230 .140876 | .051643 .110351 .152603 .845786 .902913 .869995 |
| Общая дисперсия Доля общей дисп. | 2.356684 .392781 | 2.325629 .387605 |
Интерпретация факторной структуры.Теперь картина становится более ясной. Как и ожидалось, первый фактор отмечен высокими нагрузками на переменные, связанные с удовлетворенностью на работе, а второй фактор - с удовлетворенностью домом. Из этого вы должны заключить, что удовлетворенность, измеренная вашим вопросником, составлена из двух частей: удовлетворенность домом и работой, следовательно, вы произвели классификацию переменных.
Центроидный метод
общих факторов F1,F2,...,Fk и характерного фактора Uj. При этом считается, что каждый общий фактор имеет существенное значение для анализа всех… Основные предположения факторного анализа связаны с допущением о линейности… X1 =a11F1+...+a1kF1k+d1U1Метод экстремальной группировки параметров
Формально задача об одновременной группировке параметров и выделении существенных факторов заключается в максимизации как по разбиению параметров на… ,Критерии рационального выбора числа факторов
Критерий Кайзера.Сначала вы можете отобрать только факторы, с собственными значениями, большими 1. По существу, это означает, что если фактор не… Критерий каменистой осыпи.Критерий каменистой осыпи является графическим… Кэттель предложил найти такое место на графике, где убывание собственных значений слева направо максимально…Общие выводы
Результаты факторного анализа будут успешными, если удается дать содержательную интерпретацию выявленных факторов, исходя из смысла показателей, характеризующих эти факторы. Данная стадия работы весьма ответственная; она требует от исследователя четкого представления о содержательном смысле показателей, которые привлечены для анализа и на основе которых выделены факторы. Поэтому при предварительном тщательном отборе показателей для факторного анализа следует руководствоваться их содержательным смыслом, а не стремлением к включению в анализ как можно большего их числа.
Рассмотрим несколько методических вопросов, связанных с особенностями методов факторного анализа.
а) Большинство методов факторного анализа не статистические в строгом смысле этого слова, так как для них не разработаны способы распространения выборочных результатов на генеральную совокупность. Исходную корреляционную матрицу рассматривают как заданную, а факторы выделяют без учета ошибки выборки, присущей корреляционной матрице. Исключениями являются метод максимального правдоподобия (Лоули) и канонический факторный анализ (Рао),
для которых разработаны критерии проверки значимости выделенных факторов.
При использовании других (основных) методов факторного анализа вопрос о
значимости факторных нагрузок обычно решается с помощью эмпирических порогов значимости (например, а1i > 0,3÷0,4). Содержательный смысл фактора выявляется на основе признаков, имеющих высокие (значимые) факторные нагрузки.
б) Одной из проблем факторного анализа является проблема вращения. Любое ортогональное вращение факторов приводит к такой же факторизации с перераспределением нагрузок аij, что связано с их неоднозначностью.
Необходимость вращения факторов возникает чаще всего, когда выявленным
факторам не удается дать достаточно четкую содержательную интерпретацию.
Например, факторные нагрузки для рассматриваемого фактора могут быть
близкими по величине и одинаковыми по знаку у многих признаков, так что трудно
однозначно определить, какой фактор «стоит» за выделенной комбинацией
признаков. Вращение позволяет сделать матрицу факторных нагрузок более
«контрастной» за счет увеличения нагрузок по одним признакам и уменьшения по другим, что способствует более отчетливому выявлению групп признаков, определяющих тот или иной фактор. Отметим в этой связи, что необходимость использования процедур вращения отсутствует в том случае, когда применяют метод экстремальной группировки параметров. Этот метод не связан ограничением ортогональности факторов, поэтому при его использовании получают факторы, максимально приближенные к «пучкам» взаимосвязанных показателей. В методе экстремальной группировки параметров факторные нагрузки имеют, как правило, весьма высокие значения, так как в этом методе факторные нагрузки признаков, относящихся к одному фактору, зависят от коэффициентов корреляции только между признаками данной группы.
в)Одно из ограничений на использование факторного анализа заключается в том, что используемые в этом виде анализа признаки должны быть количественными. В последние годы внимание к разработке методов факторизации качественных признаков возрастает, появились первые работы в этом направлении (в Четности, факторный анализ соответствий, аналог метода главных компонент и др.).
Ошибки использования ФА можно условно разделить на две части: ошибки применения и ошибки описания. В первом случае авторы достаточно подробно описывают процедуру ФА, не понимая при этом, что выполненный ими анализ ошибочен, поскольку авторская реализация противоречит основным положения ФА. Во втором случае авторы просто констатируют факт сам использования ФА, не сообщая читателю достаточной информации, необходимой для критической оценки надёжности описываемых выводов. Ясно, что в этом случае даже корректно выполненный ФА может не достичь своей цели, поскольку читатель не имеет возможности оценить по достоинству описанные результаты.
Список литературы:
1. Кули, Лонес. Факторный анализ, 1971.
2. Линдеман, Меренда. Факторный анализ, 1980.
3. Моррисон, Мулэйк. Факторный анализ, 1972.
4. Стивене. Факторный анализ, 1986.
5. Фишер Р.А. Статистические методы для исследователей, 1958.
6. Харман Г.Г. Современный факторный анализ, 1972.
7. Ширяев А.Н. Статистический последовательный анализ, 1976.
Подгонка функций распределения
Проверка качественных характеристик выборки
Любой статистически критерий проверки гипотез представляет собой средство измерения. Поэтому пользоваться им следует также квалифицированно, как и… С необходимостью решения задач проверки гипотез о принадлежности двух выборок… Среди множества статистических критериев, параметрических и непараметрических, используемых для проверки…Критерий Смирнова
. При практическом использовании критерия значение статистики рекомендуется… ,Критерий однородности Лемана-Розенблатта
, где – эмпирическая функция распределения, построенная по вариационному ряду… , (3)Вывод
Сравнивая мощность критериев относительно рассмотренных альтернатив с учетом действительных уровней значимости критерия Смирнова (табл. 2), можно заметить, что, как правило, мощность критерия Лемана-Розенблатта заметно выше мощности критерия Смирнова. Однако относительно очень близких альтернатив несколько выше оказывается мощность критерия Смирнова (см. мощность относительно альтернативы H5). Последнее становится интуитивно понятным, если вспомнить, что в критерии Смирнова мера отклонения линейная, а в критерии Лемана-Розенблатта – квадратичная.
Таблица 3. Мощность критерия однородности Лемана–Розенблатта относительно альтернатив H1÷H5 в зависимости от объемов выборок (m=n)
Уровень значимости 
| Значения мощности относительно альтернативы 
| ||||||
| n=20 | n=50 | n=100 | n=300 | n=500 | n=1000 | n=2000 | |
| 0,1 | 0,1241 | 0,1382 | 0,1727 | 0,3125 | 0,4369 | 0,6874 | 0,9114 |
| 0,05 | 0,0615 | 0,0770 | 0,0999 | 0,2078 | 0,3211 | 0,5703 | 0,8469 |
| 0,025 | 0,0324 | 0,0410 | 0,0590 | 0,1333 | 0,2288 | 0,4589 | 0,7681 |
Значения мощности относительно альтернативы 
| |||||||
| 0,1 | 0,4321 | 0,7628 | 0,9549 | ||||
| 0,05 | 0,3121 | 0,6473 | 0,9154 | ||||
| 0,025 | 0,2120 | 0,5355 | 0,8661 | 0,9998 | |||
Значения мощности относительно альтернативы 
| |||||||
| 0,1 | 0,1096 | 0,1107 | 0,1147 | 0,1459 | 0,1898 | 0,3265 | 0,6237 |
| 0,05 | 0,0508 | 0,0567 | 0,0563 | 0,0691 | 0,0945 | 0,1675 | 0,3986 |
| 0,025 | 0,0252 | 0,0291 | 0,0283 | 0,0334 | 0,0442 | 0,0805 | 0,2259 |
Значения мощности относительно альтернативы 
| |||||||
| 0,1 | 0,1655 | 0,2875 | 0,5513 | 0,9875 | 0,9999 | ||
| 0,05 | 0,0801 | 0,1437 | 0,3199 | 0,9470 | 0,9993 | ||
| 0,025 | 0,0361 | 0,0727 | 0,1687 | 0,8587 | 0,9952 | ||
Значения мощности относительно альтернативы 
| |||||||
| 0,1 | 0,1087 | 0,1069 | 0,1135 | 0,1422 | 0,1826 | 0,2978 | 0,5463 |
| 0,05 | 0,0511 | 0,0549 | 0,0581 | 0,0668 | 0,0910 | 0,1450 | 0,3390 |
| 0,025 | 0,0241 | 0,0276 | 0,0290 | 0,0332 | 0,0431 | 0,0712 | 0,1822 |
При обработке результатов измерений, в задачах статистического управления качеством обычно имеют дело с выборками достаточно ограниченного или, чаще, малого объема. Следует отчетливо понимать, что критерии однородности вследствие низкой мощности при малых объемах выборок не способны различать близкие альтернативы. Поэтому проверяемая гипотеза об однородности выборок, даже в случае ее несправедливости, чаще не будет отклоняться. Сдвиг на  или увеличение масштабного параметра (рассеяния) на 10% при малых объемах выборок критерии однородности вернее всего “не заметят”, но большие отклонения в законах, соответствующих выборкам, будут отмечаться. Например, для того чтобы в случае применения критерия Лемана-Розенблатта вероятности ошибок 1-го
или увеличение масштабного параметра (рассеяния) на 10% при малых объемах выборок критерии однородности вернее всего “не заметят”, но большие отклонения в законах, соответствующих выборкам, будут отмечаться. Например, для того чтобы в случае применения критерия Лемана-Розенблатта вероятности ошибок 1-го  и 2-го рода
и 2-го рода  не превышали 0.1 при наличии сдвига
не превышали 0.1 при наличии сдвига  (альтернативаH1) объемы выборок должны быть порядка 2000. А при сдвиге
(альтернативаH1) объемы выборок должны быть порядка 2000. А при сдвиге  (Альтернатива H2) вероятности ошибок не превысят величин 0.1 при объемах выборок не более 100.
(Альтернатива H2) вероятности ошибок не превысят величин 0.1 при объемах выборок не более 100.
Так как распределение статистики (3) очень быстро сходится к распределению 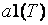 , то использование его в качестве распределения статистики критерия Лемана-Розенблатта корректно и при малых m,n.
, то использование его в качестве распределения статистики критерия Лемана-Розенблатта корректно и при малых m,n.
В случае критерия Смирнова из-за ступенчатого характера распределения статистики (1) (особенно при n=m) использование предельного распределения Колмогорова 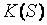 для экспериментатора будет связано с очень приблизительным знанием действительного уровня значимости (вероятности ошибки 1-го рода) и соответствующего критического значения. Поэтому при построении процедур проверки однородности по критерию Смирнова рекомендуется: 1) выбирать
для экспериментатора будет связано с очень приблизительным знанием действительного уровня значимости (вероятности ошибки 1-го рода) и соответствующего критического значения. Поэтому при построении процедур проверки однородности по критерию Смирнова рекомендуется: 1) выбирать  так, чтобы они представляли собой взаимно простые числа, а их наименьшее общее кратное k было максимальным и равным mn; 2) использовать в критерии Смирнова статистику вида (2). Тогда применение распределения Колмогорова в качестве распределения статистики (2) критерия Смирнова будет корректным при относительно малых
так, чтобы они представляли собой взаимно простые числа, а их наименьшее общее кратное k было максимальным и равным mn; 2) использовать в критерии Смирнова статистику вида (2). Тогда применение распределения Колмогорова в качестве распределения статистики (2) критерия Смирнова будет корректным при относительно малых  и
и  .
.
Подводя итоги и учитывая результаты сравнительного анализа мощности и особенности применения, для проверки однородности целесообразно рекомендовать применение и того, и другого критерия.
Метод минимального расстояния
где - функция распределения случайной величины X. Эти свойства таковы: 1)p(G(X), G(Y)) = p(X, Y) для любой непрерывной и строго монотонной функции G{x) на ;Проверка количественных характеристик выборки
На данном этапе имеется функция распределения, которая визуально похожа на некоторое уже известное распределение. Но необходимо описать эту близость… Итак , начнем с рассмотрения критериев согласия. Критерий Согласияприменяется в задаче проверки согласия, суть которой заключается в следующем. Пусть X1, Х2, ..., Хn…Список литературы
1. Лемешко Б.Ю., Помадин С.С. Проверка гипотез о математических ожиданиях и дисперсиях в задачах метрологии и контроля качества при вероятностных законах, отличающихся от нормального // Метрология. 2004. – № 3.- С.3-15.
2. Лемешко Б.Ю., Лемешко С.Б., Миркин Е.П. Исследование критериев проверки гипотез, используемых в задачах управления качеством // Материалы VII международной конференции “Актуальные проблемы электронного приборостроения” АПЭП-2004. Новосибирск, 2004. – Т. 6. – С. 269-272.
3. Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. – М.: Наука, 1983. – 416 с.
4. Лемешко Б.Ю., Миркин Е.П. Критерии Бартлетта и Кокрена в измерительных задачах при вероятностных законах, отличающихся от нормального // Измерительная техника. 2004. № 10. – С. 10-16.
5. Орлов А.И. О проверке однородности двух независимых выборок // Заводская лаборатория. – 2003. – Т.69. №.1. – С.55-60.
6. Смирнов Н.В. Оценка расхождения между эмпирическими кривыми распределения в двух независимых выборках // Бюллетень МГУ, серия А. – 1939. – Т.2. №2. – С.3-14.
7. Боровков А.А. К задаче о двух выборках // Изв. АН СССР, серия матем., 1962. Т. 26. – С.605-624.
8. Королюк В.С. Асимптотический анализ распределений максимальных уклонений в схеме Бернулли // Теория вероятностей и ее применения. – 1959. – Т.4. – С. 369-397.
9. Смирнов Н.В. Вероятности больших значений непараметрических односторонних критериев согласия // Труды Матем. ин-та АН СССР. – 1961. – Т.64. – С. 185-210.
10. Lehmann E.L. Consistency and unbiasedness of certain nonparametric tests / Ann. Math. Statist. – 1951. V.22. № 1. – P.165-179.
11. Rosenblatt M. Limit theorems associated with variants of the von Mises statistic // Ann. Math. Statist. – 1952. V.23. – P.617-623.
12. Энциклопедический словарь Вероятность и математическая статистика.
13. А.Н. Ширяев Вероятность // Изд. МЦНМО – 2004. – Ч1. – С. 448-490.
Кластерный анализ
Сущность, типологизация и прикладная направленность задач классификации объектов
"Кластерный анализ" — научное направление предназначенное для формирования групп "близких" между собой объектов по совокупности общих для этих объектов признаков. По смыслу аналогичен терминам: автоматическая классификация, таксономия, распознавание образов без учителя. Фактически "кластерный анализ" - это обобщенное название достаточно большого набора алгоритмов, используемых при создании классификации. В ряде изданий используются и такие синонимы кластерного анализа, как классификация и разбиение. Кластерный анализ широко используется в науке как средство типологического анализа. В любой научной деятельности классификация является одной из фундаментальных составляющих, без которой невозможны построение и проверка научных гипотез и теорий. Анализ отечественных и зарубежных публикаций показывает, что кластерный анализ находит применение в самых разнообразных научных направлениях: в биологии, медицине, археологии, истории, географии, экономике, психологии, социологии, филологии, политике и т.д. В прекрасной книге В.В. Налимова "Вероятностная модель языка" описано применение кластерного анализа при исследовании восприятия живописи.
Необходимость анализа и формализации задач, связанных со сравнением и классификацией объектов, сознавали учёные далёкого прошлого. "Его (Аристотеля) величайшим и в то же время чреватым наиболее опасными последствиями вкладом в науку была идея классификации, которая проходит через все его работы ... Аристотель ввёл или, по крайней мере, кодифицировал способ классификации предметов, основанный на сходстве и различии ...", - писал Дж. Берналл в "Науке истории общества" (М,: Изд-во иностр. лит., 1956, с. 117).
После Аристотеля с его "деревом вещей жизни" имеется (ещё в докомпьютерной эре) ряд интереснейших примеров прекрасно построенных классификаций как в естественных, так и в общественных науках. Иерархическая классификация (основанная на понятии сходства) растений и видов М. Адансона (1757 г.). Знаменитая периодическая система элементов Д.И. Менделеева (1869 г.), представляющая собой по существу классификацию многомерных наблюдений (каждый химический элемент может представлен в виде вектора характеризующих его разнотипных признаков, включая характеристики конфигурации внешних электронных оболочек атомов) с выявленным единым классифицирующим фактором (зарядом атомного ядра) и с упорядочением элементов внутри каждого класса.
Большая часть литературы по кластерному анализу появилась в течение последних трех десятилетий, хотя первые работы, в которых упоминались кластерные методы, известны достаточно давно. Польский антрополог К. Чекановский выдвинул идею "структурной классификации", содержавшую основную идею кластерного анализа - выделение компактных групп объектов. В 1925 г. советский гидробиолог П.В. Терентьев разработал так называемый "метод корреляционных плеяд", предназначенный для группирующих признаков. Этот метод дал толчок развитию способов группировки с помощью графов.
Слово "cluster" переводится с английского языка как "гроздь, кисть, пучок, группа". По этой причине первоначальное время этот вид анализа называли "гроздевым анализом". В начале 50-х годов появились публикации Р. Люиса, Е. Фикса и Дж. Ходжеса по иерархическим алгоритмам кластерного анализа. Заметный толчок развитие работ по кластерному анализу дали работы Р.Розенблатта по распознающему устройству (персептрону), положившие начало развитию теории "распознавания образов без учителя".
Толчком к разработке современных методов классификации и к появлению нового научного направления под названием "Кластерный анализ" явилась книга "Принципы численной таксономии", опубликованная в 1963 г. двумя биологами — Робертом Сокэлом и Питером Снитом. Авторы этой книги исходили из того, что для создания эффективных биологических классификаций, процедура кластеризации должна обеспечивать использование всевозможных показателей-признаков характеризующих исследуемые организмы, производить оценку степени сходства между этими организмами и обеспечивать размещение схожих организмов в одну и ту же группу - кластер. При этом сформированные группы должны быть достаточно «локальны», т.е. сходство объектов внутри групп должно превосходить сходство групп между собой. Последующий анализ выделенных групп-кластеров, по мнению авторов, может выяснить, отвечают ли эти группы разным биологическим видам. Иными словами, Сокэл и Снит предполагали, что выявление структуры распределения объектов в группы, помогает установить процесс образования этих групп. Различие и сходство организмов разных кластеров (групп) могут служить базой для осмысления происходившего эволюционного процесса и выяснения его механизма.
После появления книги Сокэла и Снита идеи кластерного анализа стремительно начали использоваться во многих других научных направлениях. Большая часть литературы по кластерному анализу появилась в течение последних трёх десятилетий ХХ-го столетия. Достаточно сказать, что только число монографий по кластерному анализу, изданных к настоящему времени в разных странах, измеряется сотнями. И это вполне понятно. Ведь речь идёт фактически о моделировании операции группирования - одной из важнейших не только в статистике, но и в познании, распознавании образов, принятии управленческих и иных решений. По приблизительным оценкам специалистов число публикаций по кластерному анализу и его приложениям в различных областях знаний удваивается каждые три года.
Каковы же причины столь бурного интереса к этому виду анализа? Объективно существуют три основные причины этого явления.
Первая- это появление мощной вычислительной техники, без которой кластерный анализ реальных данных практически не реализуем.
До разработки аппарата многомерного статистического анализа и, главное, до появления и развития достаточно мощной электронной вычислительной базы проблемы теории и практики классификации относились не к разработке методов и алгоритмов, а к полноте и тщательности отбора и теоретического анализа изучаемых объектов, характеризующих их общих признаков, смысла и числа градаций по каждому из них. Вследствие этого субъективная классификация, которая ранее опиралась па достаточно малое количество учитываемых признаков, часто оказывается ненадёжной. Объективная классификация, с всё возрастающим набором признаков, характеризующих изучаемые объекты, требует использования сложных алгоритмов кластеризации, которые могут быть реализованы только на базе современных компьютеров. Именно электронно-вычислительная техника стала тем главным инструментом, который позволил но новому подойти к решению этой важной проблемы и, в частности, конструктивно воспользоваться некоторым уже разработанным и разрабатываемым аппаратам многомерного статистического анализа объектов произвольной природы.
Следующая причиназаключается в том, что современная наука всё сильнее опирается в своих построениях на классификацию. Причём этот процесс всё более углубляется, поскольку параллельно этому идет всё большая специализация знания, которая невозможна без достаточно объективной классификации.
По мере роста объема перерабатываемой информации и, в частности, числа классифицируемых объектов и характеризующих их признаков возможность эффективной реализации подобной логики исследования становилась всё менее реальной. Так, например, число к групп или классов, подсчитываемое при комбинационной группировке по формуле:
где nij - число градаций по признаку ,
р - общее число анализируем их признаков,
уже при nij =3 и р = 5 оказывается равным 243. Именно электронно-вычислительная техника стала тем инструментом, который позволил по новому подойти к решению этой важной проблемы и, в частности, конструктивно воспользоваться разрабатываемым в настоящее время аппаратом обработки многомерных статистических объектов как числовой, так и нечисловой природы.
До появления современной компьютерной техники все методы классификации сводились по существу к методике группировки объектов по некоторому ограниченному числу признаков, которые характеризовались только значениями, поддающимися их количественному измерению (измерению числом). Однако оказалось, что большая половина признаков, особенно в экономике, социологии, психологии, политологии идр. не поддаются числовому измерению. В связи с этим, в последние три десятилетия появилось новое, но пока ещё недостаточно изученное направление под названием "статистика объектов нечисловой природы". В настоящей работе этому направлению уделяется главное внимание.
Появление средств обработки больших массивов данных стимулировало проведение комплексных исследований сложных многомерных социально-экономических, технических, медицинских и многих других процессов и систем. Таких, как образ и уровень жизни населения, которые так же характеризуются набором признаков как числовой, так и нечисловой природы, совершенствование организационных систем, региональная дифференциация социально-экономического развития, планирование и прогнозирование отраслевых систем, выявление закономерностей возникновения сбоев в технике, классификация заболеваний в медицине, в археологии с использованием кластерного анализа исследователи пытаются установить таксономии каменных орудий, похоронных объектов. Известны широкие применения кластерного анализа в маркетинговых исследованиях. В общем, всякий раз, когда необходимо классифицировать "горы" информации к пригодным для дальнейшей обработки группам, кластерный анализ оказывается весьма полезным и эффективным.
Третья причина- углубление специальных знаний неизбежно приводит кувеличению количества переменных или признаков, учитываемых при анализе тех или иных объектов или явлений.
Кластерный анализ предназначен для разбиения множества объектов на заданное или неизвестное число классов на основании некоторого математического критерия качества. Узловым моментом в кластерном анализе считается выбор топометрики (или нормы близости объектов), от которой решающим образом зависит окончательный вариант разбиения объектов на группы при заданном алгоритме разбиения.
Но до настоящего времени учёные так и не пришли к единому мнению по выбору имманентной метрики. В каждом научном направлении и каждой конкретной задаче этот выбор производится по-своему, с учетом главных целей исследования, физической и статистической природы используемой информации и т. п.
Кластерный анализ в задачах социально-экономического прогнозирования
- однородных групп населения по различным аспектам жизне- деятельности или образа жизни в целом; - групп детей или взрослых с общими для них характерными признаками;Кластерный анализ как инструмент подготовки эффективных маркетинговых решений
Действительно, понять и, тем более, количественно описать покупательское поведение — задача нетривиальная. Наибольшую сложность представляет то, что… Как известно, любая технология хороша тем, что регламентирует все необходимые… Для того, чтобы составить эффективно работающие рекламные материалы и медиаплан необходимо знать предпочтения…Методы кластерного анализа
Методы кластерного анализа можно разделить на две группы:
•иерархические;
•не иерархические.
Каждая из групп включает множество подходов и алгоритмов.
Используя различные методы кластерного анализа, аналитик может получить различные решения для одних и тех же данных. Это считается нормальным явлением.
Рассмотрим иерархические и неиерархические методы подробно.
Иерархические методы кластерного анализа
Иерархические агломеративные методы (Agglomerative Nesting, AGNES) Эта группа методов характеризуется последовательным объединением исходных элементов и соответствующим уменьшением…Дендрограмма (dendrogram) — древовидная диаграмма, содержащая n уровней, каждый из которых соответствует одному из шагов процесса последовательного укрупнения кластеров.
Дендрограмму также называют древовидной схемой, деревом объединения кластеров, деревом иерархической структуры.
Дендрограмма представляет собой вложенную группировку объектов, которая изменяется на различных уровнях иерархии.
Существует много способов построения дендограмм. В дендограмме объекты могут располагаться вертикально или горизонтально. Пример вертикальной дендрограммы приведен на рис. 13.4.
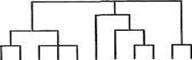
11 10 3 4 5 1 7 8 9 2 6
Рис. 13.4. Пример дендрограммы
Числа 11, 10, 3 и т.д. соответствуют номерам объектов или наблюдений исходной выборки. Мы видим, что на первом шаге каждое наблюдение представляет один кластер (вертикальная линия), на втором шаге наблюдаем объединение таких наблюдений: 11и10;3,4и5;8и9; 2 и 6. На втором шаге продолжается объединение в кластеры: наблюдения 11,10,3,4,5 и 7,8,9. Данный процесс продолжается до тех пор, пока все наблюдения не объединятся в один кластер.
Меры сходства
Для придания больших весов более отдаленным друг от друга объектам можем воспользоваться квадратом Евклидова расстояния путем возведения в квадрат… Манхэттенское расстояние (расстояние городских кварталов), также называемое… Расстояние Чебышева: это расстояние стоит использовать, когда необходимо определить два объекта как…Методы объединения или связи
Метод ближнего соседа или одиночная связь: здесь расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами… Метод наиболее удаленных соседей, или полная связь. Здесь расстояния между… Метод Варда (Ward's method): в качестве расстояния между кластерами берется прирост суммы квадратов расстояний…Иерархический кластерный анализ в SPSS
В этом методе реализуется иерархический агломеративный алгоритм, смысл которого заключается в следующем. Перед началом кластеризации все объекты… Для определения расстояния между парой кластеров могут быть сформулированы… • Среднее расстояние между кластерами (Between-groups linkage), устанавливается по умолчанию.Определение количества кластеров
Процессу группировки объектов в иерархическом кластерном анализе соответствует постепенное возрастание коэффициента, называемого критерием Е.… В таблице 13.2 мы видим, что значение поля Coefficients увеличивается… В нашем примере — это скачок с 1,217 до 7,516. Оптимальным считается количество кластеров, равное разности количества…Итеративные методы
Рассмотрены итеративные методы на примере алгоритма k-средних. Описан процесс кластерного анализа. Приведен сравнительный анализ иерархических и неиерархических методов и некоторые новые алгоритмы.
При большом количестве наблюдений иерархические методы кластерного анализа не пригодны. В таких случаях используют неиерархические методы, основанные на разделении, которые представляют собой итеративные методы дробления исходной совокупности. В процессе деления новые кластеры формируются до тех пор, пока не будет выполнено правило остановки.
Такая неиерархическая кластеризация состоит в разделении набора данных на определенное количество отдельных кластеров. Существует два подхода. Первый заключается в определении границ кластеров как наиболее плотных участков в многомерном пространстве исходных данных, т.е. определение кластера там, где имеется большое "сгущение точек". Второй подход заключается в минимизации меры различия объектов
Алгоритм k-средних (k-means)
Наиболее распространен среди неиерархических методов алгоритм k- средних, также называемый быстрым кластерным анализом. Полное описание алгоритма можно найти в работе Хартигана и Вонга (Hartigan and Wong, 1978). В отличие от иерархических методов, которые не требуют предварительных предположений относительно числа кластеров, для возможности использования этого метода необходимо иметь гипотезу о наиболее вероятном количестве кластеров.
Алгоритм k-средних строит k кластеров, расположенных на возможно больших расстояниях друг от друга. Основной тип задач, которые решает алгоритм k-средних, — наличие предположений (гипотез) относительно числа кластеров, при этом они должны быть различны настолько, насколько это возможно. Выбор числа к может базироваться на результатах предшествующих исследований, теоретических соображениях или интуиции
Общая идея алгоритма: заданное фиксированное число к кластеров наблюдения сопоставляются кластерам так, что средние в кластере (для всех переменных) максимально возможно отличаются друг от друга.
Описание алгоритма.
Первоначальное распределение объектов по кластерам.
Выбирается число k, и на первом шаге эти точки считаются "центрами" кластеров. Каждому кластеру соответствует один центр.
Выбор начальных центроидов может осуществляться следующим образом:
•выбор k-наблюдений для максимизации начального расстояния;
•случайный выбор k -наблюдений;
•выбор первых k -наблюдений.
В результате каждый объект назначен определенному кластеру.
Итеративный процесс.
Процесс вычисления центров и перераспределения объектов продолжается до тех пор, пока не выполнено одно из условий: •кластерные центры стабилизировались, т.е. все наблюдения принадлежат… •число итераций равно максимальному числу итераций.Проверка качества кластеризации
Достоинства алгоритма k -средних: •простота использования; •быстрота использования;Сравнительный анализ иерархических и неиерархических методов кластеризации.
Неиерархические методы выявляют более высокую устойчивость по отношению к шумам и выбросам, некорректному выбору метрики, включению незначимых… Если нет предположений относительно числа кластеров, рекомендуют использовать… Иерархические методы, в отличие от неиерархических, отказываются от определения числа кластеров, а строят полное…Новые алгоритмы и некоторые модификации алгоритмов кластерного анализа
Однако сейчас, в связи с появление сверхбольших баз данных, появились новые требования, которым должен удовлетворять алгоритм кластеризации.… Отметим также другие свойства, которым должен удовлетворять алгоритм… В последнее время ведутся активные разработки новых алгоритмов кластеризации, способных обрабатывать сверхбольшие базы…Алгоритм BIRCH
Алгоритм предложен Тьян Зангом и его коллегами. Благодаря обобщенным представлениям кластеров, скорость кластеризации… В этом алгоритме реализован двухэтапный процесс кластеризации.Алгоритм WaveCluster
Главные особенности WaveCluster: 1. сложность реализации; 2. алгоритм может обнаруживать кластеры произвольных форм;Алгоритмы Clarans, CURE, DBScan
Среди новых масштабируемых алгоритмов также можно отметить алгоритм CURE — алгоритм иерархической кластеризации и алгоритм DBScan , где понятие… Основным недостатком алгоритмов BIRCH, Clarans, CURE, DBScan является то… Над масштабируемыми методами сейчас активно работают многие исследователи, основная задача которых — преодолеть…Дисперсионный анализ
Введение
Дисперсионный анализ (ДА) (от латинского Dispersio – рассеивание) – статистический метод, позволяющий анализировать влияние различных факторов на исследуемую переменную. Метод был разработан биологом Р. Фишером в 1925 году и применялся первоначально для оценки экспериментов в растениеводстве. В дальнейшем выяснилась общенаучная значимость ДА для экспериментов в психологии, педагогике, медицине и др.
Целью ДА является проверка значимости различия между средними с помощью сравнения дисперсий. Дисперсию измеряемого признака разлагают на независимые слагаемые, каждое из которых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение таких слагаемых позволяет оценить значимость каждого изучаемого фактора, а также их комбинации.
При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии.
При проведении исследования рынка часто встает вопрос о сопоставимости результатов. Например, проводя опросы по поводу потребления какого-либо товара в различных регионах страны, необходимо сделать выводы, на сколько данные опроса отличаются или не отличаются друг от друга. Сопоставлять отдельные показатели не имеет смысла и поэтому процедура сравнения и последующей оценки производится по некоторым усредненным значениям и отклонениям от этой усредненной оценки. Изучается вариация признака. За меру вариации может быть принята дисперсия. Дисперсия σ2 – мера вариации, определяемая как средняя из отклонений признака, возведенных в квадрат.
На практике часто возникают задачи более общего характера – задачи проверки существенности различий средних выборочных нескольких совокупностей. Например, требуется оценить влияние различного сырья на качество производимой продукции, решить задачу о влиянии количества удобрений на урожайность с/х продукции.
Иногда ДА применяется, чтобы установить однородность нескольких совокупностей (дисперсии этих совокупностей одинаковы по предположению; если ДА покажет, что и математические ожидания одинаковы, то в этом смысле совокупности однородны). Однородные же совокупности можно объединить в одну и тем самым получить о ней более полную информацию, следовательно, и более надежные выводы.
Дисперсионный анализ
Основные понятия дисперсионного анализа.
В процессе наблюдения за исследуемым объектом качественные факторы произвольно или заданным образом изменяются. Конкретная реализация фактора (например, определенный температурный режим, выбранное оборудование или материал) называется уровнем фактора или способом обработки. Модель ДА с фиксированными уровнями факторов называют моделью I, модель со случайными факторами - моделью II. Благодаря варьированиюфактора можно исследовать его влияние на величину отклика. В настоящее время общая теория ДА разработана для моделей I.
В зависимости от количества факторов, определяющих вариацию результативного признака, ДА подразделяют на однофакторный и многофакторный.
Основными схемами организации исходных данных с двумя и более факторами являются:
- перекрестная классификация, характерная для моделей I, в которых каждый уровень одного фактора сочетается при планировании эксперимента с каждой градацией другого фактора;
- иерархическая (гнездовая) классификация, характерная для модели II, в которой каждому случайному, наудачу выбранному значению одного фактора соответствует свое подмножество значений второго фактора.
Если одновременно исследуется зависимость отклика от качественных и количественных факторов, т.е. факторов смешанной природы, то используется ковариационный анализ.
При обработке данных эксперимента наиболее разработанными и поэтому распространенными считаются две модели. Их различие обусловлено спецификой планирования самого эксперимента. В модели ДА с фиксированными эффектами исследователь намеренно устанавливает строго определенные уровни изучаемого фактора. Термин «фиксированный эффект» в данном контексте имеет тот смысл, что самим исследователем фиксируется количество уровней фактора и различия между ними. При повторении эксперимента он или другой исследователь выберет те же самые уровни фактора. В модели со случайными эффектами уровни значения фактора выбираются исследователем случайно из широкого диапазона значений фактора, и при повторных экспериментах, естественно, этот диапазон будет другим.
Таким образом, данные модели отличаются между собой способом выбора уровней фактора, что, очевидно, в первую очередь влияет на возможность обобщения полученных экспериментальных результатов. Для ДА однофакторных экспериментов различие этих двух моделей не столь существенно, однако в многофакторном дисперсионном анализе оно может оказаться весьма важным.
При проведении ДА должны выполняться следующие статистические допущения: независимо от уровня фактора величины отклика имеют нормальный (Гауссовский) закон распределения и одинаковую дисперсию. Такое равенство дисперсий называется гомогенностью. Таким образом, изменение способа обработки сказывается лишь на положении случайной величины отклика, которое характеризуется средним значением или медианой. Поэтому все наблюдения отклика принадлежат сдвиговому семейству нормальных распределений.
Говорят, что техника ДА является "робастной". Этот термин, используемый статистиками, означает, что данные допущения могут быть в некоторой степени нарушены, но несмотря на это, технику можно использовать.
При неизвестном законе распределения величин отклика используют непараметрические (чаще всего ранговые) методы анализа.
В основе ДА лежит разделение дисперсии на части или компоненты. Вариацию, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия σ2. Она является мерой вариации частных средних по группам 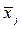 вокруг общей средней
вокруг общей средней  и определяется по формуле:
и определяется по формуле:
 ,
,
где k - число групп;
nj - число единиц в j-ой группе;
 - частная средняя по j-ой группе;
- частная средняя по j-ой группе;
 - общая средняя по совокупности единиц.
- общая средняя по совокупности единиц.
Вариацию, обусловленную влиянием прочих факторов, характеризует в каждой группе внутригрупповая дисперсия σj2.
 .
.
Между общей дисперсией σ02, внутригрупповой дисперсией σ2 и межгрупповой дисперсией  существует соотношение:
существует соотношение:
σ02 =  + σ2.
+ σ2.
Внутригрупповая дисперсия объясняет влияние неучтенных при группировке факторов, а межгрупповая дисперсия объясняет влияние факторов группировки на среднее значение по группе.
Однофакторный дисперсионный анализ.
Однофакторная дисперсионная модель имеет вид: xij = μ + Fj + εij, (1)Многофакторный дисперсионный анализ
Общая схема двухфакторного эксперимента, данные которого обрабатываются ДА имеет вид:Применение дисперсионного анализа в различных процессах и исследованиях
Использование дисперсионного анализа при изучении миграционных процессов.
λij=ciqijaj, где λij – интенсивность переходов из исходной группы i (выхода) в новую j… ci – возможность и способности покинуть группу i (ci≥0);Принципы математико-статистического анализа данных медико-биологических исследований.
ДА позволяет определить влияние разных факторов (условий) на исследуемый признак (явление), что достигается путем разложения совокупной изменчивости… С помощью ДА исследуются угрозы заболевания при наличии факторов риска.…Биотестирование почвы
Многообразные загрязняющие вещества, попадая в агроценоз, могутпретерпевать в нем различные превращения, усиливая при этом свое токсическое… Целью исследования являлось изучение торможения хлоропластов и коэффициента… Анализ изменчивости фототаксиса в разных вариантах опыта показал достоверное влияние каждого из факторов. Доля в общей…Дисперсионный анализ в химии
ДА широко используют в различных областях науки и промышленного производства для оценки дисперсности систем (суспензий, эмульсий, золей, порошков,…Заключение
Современные приложения ДА охватывают широкий круг задач экономики, биологии и техники и трактуются обычно в терминах статистической теории выявления систематических различий между результатами непосредственных измерений, выполненных при тех или иных меняющихся условиях.
Благодаря автоматизации ДА исследователь может проводить различные статистические исследования с применение ЭВМ, затрачивая при этом меньше времени и усилий на расчеты данных. В настоящее время существует множество пакетов прикладных программ, в которых реализован аппарат дисперсионного анализа. Наиболее распространенными являются такие программные продукты как:
- MS Excel;
- Statistica;
- Stadia;
- SPSS.
В современных статистических программных продуктах реализованы большинство статистических методов. С развитием алгоритмических языков программирования стало возможным создавать дополнительные блоки по обработке статистических данных.
ДА является мощным современным статистическим методом обработки и анализа экспериментальных данных в психологии, биологии, медицине и других науках. Он очень тесно связан с конкретной методологией планирования и проведения экспериментальных исследований.
ДА применяется во всех областях научных исследований, где необходимо проанализировать влияние различных факторов на исследуемую переменную
Список используемых источников
1.Кремер Н.Ш. Теория вероятности и математическая статистика. М.: Юнити – Дана, 2002.-343с.
2.Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 2003.-523с.
3. www.sutd.ru
4. www.conf.mitme.ru
5. www.pedklin.ru
6. www.webcenter.ru
7. www.encycl.yandex.ru
8. www2.econ.msu.ru
– Конец работы –
Используемые теги: Доклады, дисциплине, дополнительные, главы, математической, статистики, Регрессионный, анализ0.102
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Доклады по дисциплине Дополнительные главы математической статистики . Регрессионный анализ. 4
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов