рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Методы нелинейного оценивания
Реферат Курсовая Конспект
Методы нелинейного оценивания
Методы нелинейного оценивания - раздел Математика, Доклады по дисциплине Дополнительные главы математической статистики . Регрессионный анализ. 4 Метод Наименьших Квадратов Функция Потерь Метод Взв...
- Метод наименьших квадратов
- Функция потерь
- Метод взвешенных наименьших квадратов
- Метод максимума правдоподобия
- Максимум правдоподобия и логит/пробит модели
- Алгоритмы минимизации функций
- Начальные значения, размеры шагов и критерий сходимости
- Штрафные функции, ограничение параметров
- Локальные минимумы
- Квази-ньютоновский метод
- Симплекс-метод
- Метод Хука-Дживиса
- Метод Розенброка
- Матрица Гессе и стандартные ошибки
4.1.Метод наименьших квадратов.
После выбора модели возникает вопрос: каким образом можно оценить эти модели? Методы линейной регрессии или дисперсионного анализа используют оценивание по методу наименьших квадратов. Основной смысл этого метода заключается в минимизации суммы квадратов отклонений наблюдаемых значений зависимой переменной от значений, предсказанных моделью. (Термин наименьшие квадраты впервые был использован в работе Лежандра - Legendre, 1805.)
Определим модель в виде 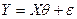 и рассмотрим способ оценки параметра
и рассмотрим способ оценки параметра  в зависимости от предположений о природе Х и характере распределения
в зависимости от предположений о природе Х и характере распределения 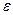 .
.
Пусть распределение вектора 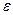 не зависит от X и нормально с нулевым вектором средних и ковариационной матрицей
не зависит от X и нормально с нулевым вектором средних и ковариационной матрицей 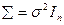 , где
, где 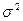 — неизвестная дисперсия компонент
— неизвестная дисперсия компонент 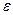 , а
, а 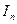 — единичная матрица порядка n. Сформулированное условие записывается
— единичная матрица порядка n. Сформулированное условие записывается  .
.
Оценка параметров данной модели проводится с помощью метода наименьших квадратов (мнк). При этом  находится из условия минимизации суммы квадратов отклонений наблюденных значений y от их сглаженных (регрессионных) значений, т.е. величины
находится из условия минимизации суммы квадратов отклонений наблюденных значений y от их сглаженных (регрессионных) значений, т.е. величины 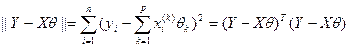 .
.
Уравнения метода наименьших квадратов в случае, когда r — ранг X равен p, имеют решение 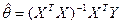 .
.
Если r<p, то в ряде случаев легко ввести дополнительные ограничения на параметры  , где ранг Н равен p - r. Пусть
, где ранг Н равен p - r. Пусть 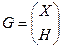 , тогда
, тогда  имеет размер
имеет размер 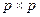 и ранг p и
и ранг p и  .
.
4.2.Функция потерь.
В стандартной множественной регрессии оценивание коэффициентов регрессии происходит “подбором” коэффициентов, минимизирующих дисперсию остатков (сумму квадратов остатков). Любые отклонения наблюдаемых величин от предсказанных означают некоторые потери в точности предсказаний, например, из-за случайного шума (ошибок). Поэтому можно сказать, что цель метода наименьших квадратов заключается в минимизации функции потерь. В этом случае, функция потерь определяется как сумма квадратов отклонений от предсказанных значений (термин функция потерь был впервые использован в работе Вальда - Wald, 1939). Когда эта функция достигает минимума, вы получаете те же оценки для параметров (свободного члена, коэффициентов регрессии), как, если бы мы использовали Множественную регрессию. Полученные оценки называются оценками по методу наименьших квадратов.
Мнк-оценкн, получающиеся в результате минимизации выборочного критерия адекватности с квадратичной функцией потерь, неустойчивы к нарушениям предположения о нормальности распределения случайных ошибок. С утяжелением «хвостов» распределения они быстро теряют свои оптимальные свойства. Это связано с тем, что квадратичная функция потерь, используемая в мнк, придает слишком большой вес далеким отклонениям от регрессионной поверхности. Прогресс в области вычислительных методов позволяет перейти к использованию функций потерь 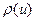 , растущих при
, растущих при  более медленно, чем
более медленно, чем  . Соответствующие оценки по сравнению с мнк-оценками более устойчивы. Определенное внимание уделяется экспоненциально-взвешенным оценкам (эв-регрессии). Они допускают простую и наглядную интерпретацию, имеют хорошие выборочные свойства в случае небольших асимметричных искажений гауссовских распределений ошибок.
. Соответствующие оценки по сравнению с мнк-оценками более устойчивы. Определенное внимание уделяется экспоненциально-взвешенным оценкам (эв-регрессии). Они допускают простую и наглядную интерпретацию, имеют хорошие выборочные свойства в случае небольших асимметричных искажений гауссовских распределений ошибок.
Функция потерь:  ,
, 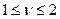 .
.
Параметры регрессионной поверхности находят из условия минимизации по вектору  :
:
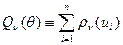 ,
,
где  . Покажем, что для
. Покажем, что для  :
:
1) решение этой задачи  единственно;
единственно;
2) в модели 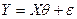 для симметричных распределений случайных ошибок оценка
для симметричных распределений случайных ошибок оценка  состоятельна.
состоятельна.
В самом деле, функция 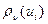 , рассматриваемая как функция от
, рассматриваемая как функция от  , строго выпукла вниз. Следовательно, строго выпукла вниз и сумма
, строго выпукла вниз. Следовательно, строго выпукла вниз и сумма 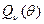 , поэтому минимум
, поэтому минимум 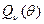 единствен и достигается в одной точке. Из строгой выпуклости
единствен и достигается в одной точке. Из строгой выпуклости 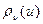 и, следовательно, положительности
и, следовательно, положительности 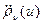 вытекает, что для любой симметричной относительно нуля случайной величины
вытекает, что для любой симметричной относительно нуля случайной величины  для любого
для любого 
 . (*)
. (*)
Из закона больших чисел следует, что в модели 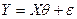 для больших значений n для любого фиксированного вектора
для больших значений n для любого фиксированного вектора 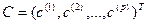
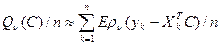 . (**)
. (**)
При симметричном относительно нуля распределении случайных ошибок, как следует из (*), правая часть (**) будет наименьшей при 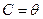 . Следовательно, в силу (**),
. Следовательно, в силу (**), 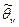 должно быть при большом n близко к
должно быть при большом n близко к  , т. е. оценка
, т. е. оценка  состоятельная.
состоятельная.
Можно также рассмотреть другие функции потерь. Например, при минимизации функции потерь, почему бы вместо суммы квадратов отклонений не рассмотреть сумму модулей отклонений? В самом деле, иногда это бывает полезно для уменьшения влияния выбросов. Влияние, оказываемое крупными остатками на всю сумму, существенно увеличивается при их возведении в квадрат. Однако если вместо суммы квадратов взять сумму модулей выбросов, влияние остатков на результирующую регрессионную кривую существенно уменьшится.
4.3.Метод взвешенных наименьших квадратов.
Третьим по распространенности методом, в дополнение к методу наименьших квадратов и использованию для оценивания суммы модулей отклонений, является метод взвешенных наименьших квадратов. Обычный метод наименьших квадратов предполагает, что разброс остатков одинаковый при всех значениях независимых переменных. Иными словами, предполагается, что дисперсия ошибки при всех измерениях одинакова. Часто, это предположение не является реалистичным. В частности, отклонения от него встречаются в бизнесе, экономике, приложениях в биологии.
Например, вы хотите изучить связь между проектной стоимостью постройки здания и суммой реально потраченных средств. Это может оказаться полезным для получения оценки ожидаемых перерасходов. В этом случае разумно предположить, что абсолютная величина перерасходов (выраженная в долларах) пропорциональна стоимости проекта. Поэтому, для подбора линейной регрессионной модели следует использовать метод взвешенных наименьших квадратов. Функция потерь может быть, например, такой (см. книгу Neter, Wasserman, and Kutner, 1985, стр.168):
Потери = (наблюд.-предск.)2 * (1/x2)
В этом уравнении первая часть функции потерь означает стандартную функцию потерь для метода наименьших квадратов (наблюдаемые минус предсказанные в квадрате; т.е., квадрат остатков), а вторая равна “весу” этой потери в каждом конкретном случае - единица деленная на квадрат независимой переменной (x) для каждого наблюдения. В ситуации реального оценивания, программа просуммирует значения функции потерь по всем наблюдениям (например, конструкторским проектам), как описано выше и подберет параметры, минимизирующие сумму. Возвращаясь к рассмотренному примеру, чем больше проект (x), тем меньше для нас значит одна и та же ошибка в предсказании его стоимости. Этот метод дает более устойчивые оценки для параметров регрессии (более подробно, см. Neter, Wasserman, and Kutner, 1985).
4.4.Метод максимума правдоподобия.
Альтернативой использования метода наименьших квадратов является поиск максимума функции правдоподобия или ее логарифма. Эквивалентным способом является минимизация логарифма функции правдоподобия со знаком минус (термин максимум правдоподобия впервые был использован в работе Фишера - Fisher, 1922a). В общем виде, функцию правдоподобия определяется так:
L = F(Y,Модель) =  in= 1 {p [yi, Параметры модели(xi)]}
in= 1 {p [yi, Параметры модели(xi)]}
Теоретически, вы можете вычислить вероятность принятия зависимой переменной определенных значений(обозначенную нами L, от слова Likelihood - правдоподобие), используя соответствующую регрессионную модель. Воспользовавшись тем, что все наблюдения независимы друг от друга, получим, что наша функция правдоподобия равна геометрической сумме ( , для всех i = 1 to n) вероятностей конкретных наблюдений (i), заданных соответствующей значению x моделью и параметрами. (Геометрическая сумма означает, что нужно перемножить вероятности по всем возможным случаям внутри скобок.) Часто эти функции представляют в виде натурального логарифма, в этом случае геометрическая сумма становится обычной арифметической суммой (
, для всех i = 1 to n) вероятностей конкретных наблюдений (i), заданных соответствующей значению x моделью и параметрами. (Геометрическая сумма означает, что нужно перемножить вероятности по всем возможным случаям внутри скобок.) Часто эти функции представляют в виде натурального логарифма, в этом случае геометрическая сумма становится обычной арифметической суммой ( , для всех i = 1 to n).
, для всех i = 1 to n).
При выборе конкретной модели, чем больше правдоподобие модели, тем больше вероятность, что предсказанное значение зависимой переменной окажется в выборке. Поэтому, чем больше правдоподобие, тем лучше модель согласуется с выборочными данными. Реальные вычисления для конкретной модели могут оказаться достаточно громоздкими, поскольку вам необходимо “отслеживать” (вычислять) вероятности появления различных значений зависимой переменной y (выбрав модель и соответствующее значение x). Оказывается, что если все предположения для стандартной множественной регрессии выполнены (они описаны в главе Множественная регрессия руководства пользователя), то стандартный метод наименьших квадратов (см. выше) дает те же оценки, что и метод максимума правдоподобия. Если предположение о постоянстве дисперсии ошибки при всех значения независимой переменной нарушено, то оценки по методу максимума правдоподобия можно получить используя метод взвешенных наименьших квадратов.
4.5.Максимум правдоподобия и пробит/логит модели.
Рассмотрим функцию правдоподобия для регрессионных моделей логит и пробит. Функция потерь для этих моделей вычисляется как сумма натуральных логарифмов логит или пробит правдоподобия L1:
log(L1) = 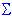 in= 1 [yi*log(pi ) + (1-yi )*log(1-pi )]
in= 1 [yi*log(pi ) + (1-yi )*log(1-pi )]
где:
log(L1) - натуральный логарифм функции правдоподобия для выбранной
(логит или пробит) модели
yi - i-ое наблюдаемое значение
pi - вероятность появления (предсказанная или подогнанная) (между 0 и 1)
Логарифм функции правдоподобия для нулевой модели (L0), т.е. модели, содержащей только свободный член (и не включающей других коэффициентов регрессии) вычисляется как:
log(L0) = n0*(log(n0/n)) + n1*(log(n1/n))
где:
log(L0) - натуральный логарифм функции правдоподобия для нулевой (логит
или пробит) модели
n0 - число наблюдений со значением 0
n1 - число наблюдений со значением 1
n - общее число наблюдений
4.6.Алгоритмы минимизации функций
Теперь, после обсуждения различных регрессионных моделей и функций потерь, используемых для их оценки, единственное, что осталось “в тайне”, это как находить минимумы функций потерь (т.е. наборы параметров, наилучшим образом соответствующие оцениваемой модели), и как вычислять стандартные ошибки оценивания параметров. Нелинейное оценивание использует очень эффективный (квази-ньютоновский) алгоритм, который приближенно вычисляет вторую производную функции потерь и использует ее при поиске минимума (т.е., при оценке параметров по соответствующей функции потерь). Кроме того, Нелинейное оценивание предлагает несколько более общих алгоритмов поиска минимума, использующих различные стратегии поиска (не связанные с вычислением вторых производных). Эти стратегии иногда более эффективны при оценивании функций потерь с локальными минимумами; поэтому, эти методы часто очень полезны для нахождения начальных значений с помощью квази-ньютоновского метода.
Во всех случаях, вы можете вычислить стандартные ошибки оценок параметров. Эти вычисления проводятся с использованием частных производных второго порядка по параметрам, которые приближенно подсчитываются с использованием метода конечных разностей.
Если вас интересует, не как именно происходит минимизация функции потерь, а только то, что такая минимизация в принципе возможна, вы можете пропустить следующие разделы. Однако они могут пригодиться, если получаемая регрессионная модель будет плохо согласовываться с данными. В этом случае, итеративная процедура может не сойтись, выдавая неожиданные (например, очень большие или очень маленькие) оценки для параметров.
В следующих параграфах, мы сначала рассмотрим некоторые вопросы, относящиеся к оптимизации без ограничений, затем дадим краткий обзор методов используемых в этом модуле. Более подробное обсуждение этих методов имеется в книгах Brent (1973), Gill and Murray (1974), Peressini, Sullivan, and Uhl (1988), и Wilde and Beightler (1967). Более широкий обзор алгоритмов можно найти в книгах Dennis and Schnabel (1983), Eason and Fenton (1974), Fletcher (1969), Fletcher and Powell (1963), Fletcher and Reeves (1964), Hooke and Jeeves (1961), Jacoby, Kowalik, and Pizzo (1972), и Nelder and Mead (1964).
– Конец работы –
Эта тема принадлежит разделу:
Доклады по дисциплине Дополнительные главы математической статистики . Регрессионный анализ. 4
Содержание... Регрессионный анализ Теоретическая часть работы...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Методы нелинейного оценивания
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов