рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Методи та приклади їх використання
Реферат Курсовая Конспект
Методи та приклади їх використання
Методи та приклади їх використання - раздел Математика, МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ В САПР Розглянемо Вантаж Маси ...
Розглянемо вантаж маси  , який коливається на пружині жорсткості
, який коливається на пружині жорсткості 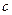 у в’язкому середовищі з коефіцієнтом в’язкості
у в’язкому середовищі з коефіцієнтом в’язкості 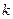 під дією періодичної сили амплітуди
під дією періодичної сили амплітуди  і частоти
і частоти 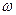 . Параметрами системи є:
. Параметрами системи є: 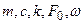 . Узагальнена координата – переміщення вантажу
. Узагальнена координата – переміщення вантажу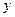 , яка є функцією параметрів та часу:
, яка є функцією параметрів та часу:
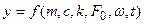 .
.
Перший спосіб отримання критеріїв подібності базується на формулі (3.2). У нашому випадку можна прийняти:  ,
, 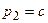 ,
,  ,
, 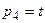 ,
, 
 ,
,  . Тоді розмірність кожної величини
. Тоді розмірність кожної величини  можна виразити наступним чином
можна виразити наступним чином
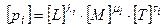 .
.
Зведемо показники степенів 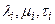 для кожної величини
для кожної величини  в таблицю.
в таблицю.
Таблиця.
| Величина | Показники степенів | ||

| 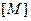
| 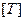
| |
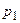
| 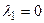
| 
| 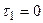
|
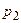
| 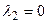
| 
| 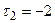
|
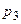
| 
| 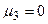
| 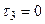
|
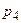
| 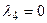
| 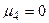
| 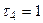
|
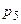
| 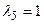
| 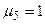
| 
|
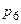
| 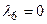
| 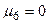
| 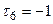
|
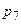
| 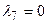
| 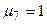
| 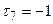
|
Система лінійних алгебраїчних рівнянь (3.1) матиме вигляд
 (3.4)
(3.4)
Ранг матриці 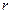 системи (3.4) рівний трьом, кількість невідомих величин
системи (3.4) рівний трьом, кількість невідомих величин 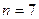 , тому система (3.4) має
, тому система (3.4) має 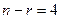 лінійно незалежних розв’язків. Це означає, що для знаходження цих розв’язків значення чотирьох величин
лінійно незалежних розв’язків. Це означає, що для знаходження цих розв’язків значення чотирьох величин 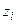 вибираються довільно, а решта величин
вибираються довільно, а решта величин 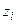 шукаються з системи (3.4).
шукаються з системи (3.4).
Нехай  ,
, 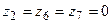 . Тоді з системи (3.4) будемо мати, що
. Тоді з системи (3.4) будемо мати, що 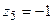 ,
,  ,
, 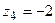 . На основі формули (3.2) отримаємо перший критерій подібності механічної коливальної системи:
. На основі формули (3.2) отримаємо перший критерій подібності механічної коливальної системи:
 .
.
Для отримання другого критерію подібності приймемо 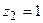 ,
,  . Тоді
. Тоді 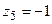 ,
,  ,
, 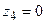 і критерій подібності буде мати вигляд
і критерій подібності буде мати вигляд 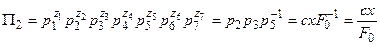 .
.
Аналогічно, прийнявши, що 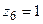 і
і 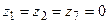 , отримаємо третій критерій подібності
, отримаємо третій критерій подібності 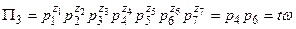 , і, нарешті, приймаючи
, і, нарешті, приймаючи 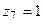 і
і  , будемо мати четвертий критерій подібності
, будемо мати четвертий критерій подібності
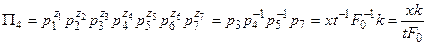 .
.
Вищенаведений метод побудови критеріїв подібності називається методом визначальних рівнянь.
Для знаходження критеріїв подібності існує декілька інших методів. Найпростіший випадок - коли задано диференційне рівняння. Для прикладу, маємо двовимірне рівняння теплопровідності 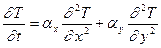 .
.
Використовуючи правило Фур’є, а саме: розмірніcть усіх членів рівняння однакова і відкидаючи знаки диференціювання розділимо всі члени рівняння на один з його членів, тобто 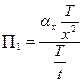 ,
,  ,
, 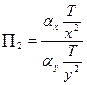 .
.
В результаті, після скорочення, отримаємо:  ,
, 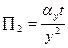 ,
,  .
.
Інший шлях знаходження критеріїв подібності - застосування методу нульових розмірностей.
[x1]=кг; [x2]=м-1; [x3]=м; [x4]=м2кг/сек2; [x5]=ceк; [x6]=сек-1.
На першому етапі виберемо три будь-які параметри, для яких визначник D¹0. Такими параметрами можуть бути х1, х2, х4.
Кг м сек
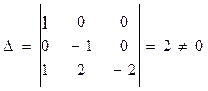 .
.
В даному випадку кількість лінійно-незалежних критеріїв подібності рівна трьом (число величин (6) мінус ранг матриці (3)).
На наступному кроці, згідно достатньої умови подібності, перший критерій подібності визначається таким чином:
1) 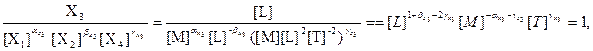
 звідки
звідки 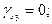
 звідки
звідки 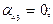
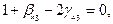 звідки
звідки 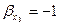 .
.
Перший критерій подібності запишеться у вигляді 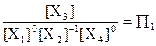 .
.
2) ,
,
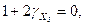 звідки
звідки 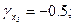
 звідки
звідки 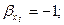
 звідки
звідки 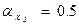 .
.
Тоді другий критерій подібності запишемо у наступній формі:
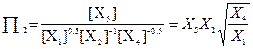 .
.
3) ,
,
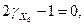 звідки
звідки 
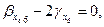 звідки
звідки 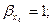
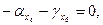 звідки
звідки 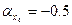 .
.
В кінцевому випадку вираз для третього критерію подібності має таку форму:
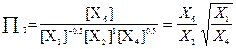 .
.
Іншим прикладом застосування теорії подібності для дослідження вихідних параметрів пристроїв в мікромасштабі.
Розглянемо переміщення рідини в трубі діаметром d, довжиною l, швидкістю v з густиною рідини ρ та коефіцієнтом в’язкості μ, і зниження тиску на цій довжині дорівнює ΔР.
Запишемо розмірності названих вище величин в системі СІ:
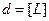 ,
, 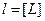 ,
, 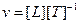 ,
,  ,
, 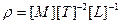 ,
, 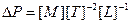 .
.
На першому етапі застосування методу нульових розмірностей виберемо три будь-які параметри, для яких значення визначника D¹0. Такими параметрами можуть бути 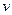 ,
, 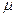 ,
,  .
.
Кг м сек
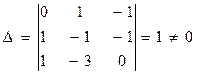 .
.
У цьому випадку кількість лінійно-незалежних критеріїв подібності дорівнює трьом (кількість величин (6) мінус ранг матриці (3)).
На наступному кроці, згідно з достатньою умовою подібності, перший критерій подібності вимагає дотримання геометричної подібності, тобто:  .
.
Другий критерій подібності визначається так:
 .
.
Маємо три рівняння та три невідомі
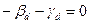 ,
, 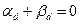 ,
, 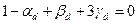 .
.
Розв’яжемо отриману систему рівнянь і отримаємо, що:
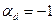 ,
, 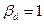 ,
, 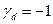 .
.
Відповідно, другий критерій подібності буде таким 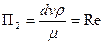 .
.
Отриманий критерій подібності  називають критерієм Рейнольдса.
називають критерієм Рейнольдса.
Третій критерій подібності визначаємо:
 .
.
Отже, 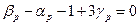 ,
, 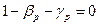 ,
, 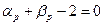 .
.
Розв’язавши систему з трьох рівнянь з трьома невідомими, отримаємо:
 ,
, 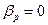 ,
, 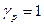 .
.
Третій критерій подібності визначається за формулою 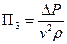 та називається критерієм Ейлера.
та називається критерієм Ейлера.
Проаналізуємо детальніше число Рейнольдса, яке є мірою турбулентності потоку (напрклад, при Re < 2000 представляє ламінарну течію і при Re > 4000 представляє турбулентну течію) та є функцією масштабу рідинної системи.
Не дивно, що, хоча ми зазвичай спостерігаємо турбулентний і хаотичний потік рідини в більшості макроскопічних систем, для потоків рідин в мікроскопічних системах майже завжди характерні умови ламінарних течій (тобто, оскільки розміри рідинної системи зменшені в 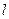 разів, то Re буде також зменшене в
разів, то Re буде також зменшене в 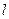 разів, тобто потік рідини стає набагато більш ламінарним в мікромасштабі порівняно з макросистемами). Фактично завдяки такій поведінці існує можливість досягнення повного змішування в мікрорідинних системах, що є дуже перспективним під час вирішення ряду технічних задач.
разів, тобто потік рідини стає набагато більш ламінарним в мікромасштабі порівняно з макросистемами). Фактично завдяки такій поведінці існує можливість досягнення повного змішування в мікрорідинних системах, що є дуже перспективним під час вирішення ряду технічних задач.
Наведемо приклад застосування методу на основі правила Фур’є до визначення вихідних теплових пристроїв в мікромасштабі. Отже, візьмемо одновимірне нестаціонарне диференціальне рівняння теплопровідності 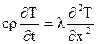 і розділимо його праву частину на ліву, при цьому опустивши знак диференціювання. Скоротивши позначення температури та підставивши замість
і розділимо його праву частину на ліву, при цьому опустивши знак диференціювання. Скоротивши позначення температури та підставивши замість  параметр довжини
параметр довжини 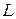 , отримаємо безрозмірний комплекс, так зване число Фур’є
, отримаємо безрозмірний комплекс, так зване число Фур’є  , який характеризує перехідний процес при перенесенні тепла та визначається з допомогою формули
, який характеризує перехідний процес при перенесенні тепла та визначається з допомогою формули 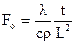 , де
, де 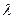 – коефіцієнт теплопровідності;
– коефіцієнт теплопровідності; 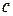 – коефіцієнт питомої теплоємності;
– коефіцієнт питомої теплоємності;  – густина матеріалу;
– густина матеріалу;  – параметр часу.
– параметр часу.
Треба додати, що число Фур’є характеризує проникнення та поширення тепла у випадку перехідного процесу при перенесенні тепла в матеріалі з коефіцієнтом теплопровідності 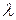 , питомою теплоємністю
, питомою теплоємністю 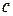 та густиною
та густиною  .
.
Отже, якщо вважати, що теплові процеси в макро- і мікропристроях подібні та їх лінійні розміри не менші за один мкм, то, відповідно, мають бути однакові значення критеріїв подібності. У нашому випадку число Фур’є для макросистеми має бути таким, як і для мікросистеми. З вищенаведеного випливає, що із зменшенням параметра довжини у 100 разів перехідний процес перенесення тепла прискорюється в 10 000 разів для постійного числа Фур’є. Тобто швидкодія зростає у 10 000 разів. Отже, отримані результати дають змогу стверджувати, що теплові актюатори в мікросвіті є достатньо швидкодіючими пристроями порівняно з тепловими макропристроями.
– Конец работы –
Эта тема принадлежит разделу:
МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ В САПР
НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ ЛЬВІВСЬКА ПОЛІТЕХНІКА... В М Теслюк МАТЕМАТИЧНЕ МОДЕЛЮВАННЯ В САПР...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Методи та приклади їх використання
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов