рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Принцип двойственности.
Реферат Курсовая Конспект
Принцип двойственности.
Принцип двойственности. - раздел Математика, КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ Пусть ...
Пусть  – некоторое подмножество множества булевых функций:
– некоторое подмножество множества булевых функций: 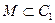 .
.
Определение 1: Множество  называется замыканием множества
называется замыканием множества  , если оно содержит все суперпозиции функций множества
, если оно содержит все суперпозиции функций множества  и не содержит никаких других функций.
и не содержит никаких других функций.
Например, если  , тогда, очевидно,
, тогда, очевидно,  .
.
Отметим очевидные свойства замыкания:
1) ;
;
2)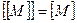 ;
;
3) если  , то
, то 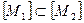 .
.
Определение 2: Множество  называется замкнутым классом, если выполняется условие:
называется замкнутым классом, если выполняется условие: 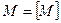 .
.
Например, пусть  . Как следует из предыдущего примера,
. Как следует из предыдущего примера, 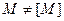 и поэтому
и поэтому  не является замкнутым классом.
не является замкнутым классом.
Если  , то класс
, то класс  является замыканием класса
является замыканием класса 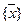 . В силу свойства 2 операции замыкания
. В силу свойства 2 операции замыкания  является замкнутым классом.
является замкнутым классом.
Очевидно, что пересечение любого числа замкнутых классов есть замкнутый класс.
Легко заметить, что если функции  содержатся в
содержатся в  то для выяснения того, является ли
то для выяснения того, является ли  замкнутым классом, достаточно ограничиться проверкой выполнения следующего условия: если функции
замкнутым классом, достаточно ограничиться проверкой выполнения следующего условия: если функции 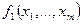 ,...,
,...,  , где
, где 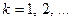 , принадлежат множеству
, принадлежат множеству  , то функция
, то функция  также принадлежит множеству
также принадлежит множеству  .
.
Определение 3: Система 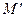 функций из замкнутого класса
функций из замкнутого класса  называется полной в
называется полной в  , если
, если 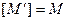 .
.
В случае если система 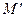 полна в
полна в  , то всякая функция из множества
, то всякая функция из множества  является суперпозицией функции из
является суперпозицией функции из 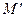 .
.
Для каждого замкнутого класса с конечным базисом введем понятие порядка замкнутого класса.
Пусть 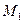 – конечный базис в
– конечный базис в  . Обозначим через
. Обозначим через 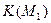 наибольший из порядков функций, принадлежащих множеству
наибольший из порядков функций, принадлежащих множеству 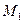 .
.
Определение 4: Порядком замкнутого класса  с конечным базисом называется такое натуральное число
с конечным базисом называется такое натуральное число  , что
, что  (здесь минимум берется по всевозможным базисам
(здесь минимум берется по всевозможным базисам 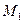 класса
класса  ).
).
Теорема 1: Конъюнкция, дизъюнкция и отрицание образуют полную систему функций в 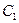 .
.
Это утверждение вытекает из следствия 2 теоремы о разложении и соотношения:  .
.
Из того, что  и
и  , а также из рассмотренной теоремы и неполноты каждой из систем
, а также из рассмотренной теоремы и неполноты каждой из систем  , получаем следующие следствия.
, получаем следующие следствия.
Следствие 1: Системы функций 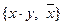 и
и  образуют базисы множества
образуют базисы множества 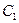 .
.
Далее, т.к. 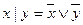 , то
, то 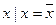 ,
,  .
.
Следствие 2: Функция  образуем базис
образуем базис 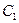 .
.
Следствие 3: Порядок класса 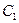 равен 2.
равен 2.
Введём в рассмотрение принцип двойственности, имеющий в дискретной математике очень важное значение.
Определение 5: Функция 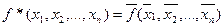 называется двойственной к функции
называется двойственной к функции  .
.
Из определения следует, что:
1) функция 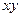 двойственна к функции
двойственна к функции 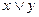 ,
,
2) функция  двойственна к функции
двойственна к функции 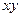 ,
,
3) функция  двойственна к функции
двойственна к функции 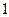 ,
,
4) функция 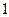 двойственна к функции
двойственна к функции  ,
,
5) функция 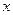 двойственна к функции
двойственна к функции 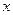 ,
,
6) функция 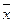 двойственна функции
двойственна функции 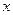 .
.
Заметим, что двойственная функция к двойственной функции есть исходная функция, т.е.  .
.
Теорема 2: (принцип двойственности). Если данная функция имеет вид:  , то двойственная ей функция:
, то двойственная ей функция: 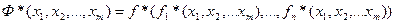 , где
, где 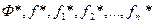 – это функции, двойственные к функциям
– это функции, двойственные к функциям  соответственно.
соответственно.
Доказательство: Имеем

Что и требовалось доказать.
Пусть  некоторое множество функций из
некоторое множество функций из 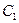 . Обозначим через
. Обозначим через 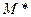 множество всех тех функций, которые являются двойственными к функциям из множества
множество всех тех функций, которые являются двойственными к функциям из множества  .
.
Определение 6: Назовем множество 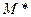 двойственным к
двойственным к  . Множество
. Множество  называется самодвойственным, если
называется самодвойственным, если  .
.
Тогда в силу принципа двойственности имеют место следующие утверждения.
Следствие 1: Если  – замкнутый класс, то
– замкнутый класс, то 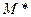 также образует замкнутый класс.
также образует замкнутый класс.
Следствие 2: Если  – замкнутый класс и система функций
– замкнутый класс и система функций 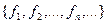 полна в
полна в  , то система
, то система  полна в
полна в 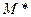 , т.е. из
, т.е. из  следует, что
следует, что 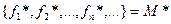 .
.
В частности, если 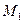 является базисом замкнутого класса
является базисом замкнутого класса  , то
, то 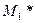 является базисом
является базисом 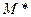 .
.
Следствие 3: Если  , то
, то 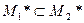 .
.
Определение 7: Функция 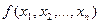 называется самодвойственной, если
называется самодвойственной, если 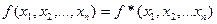 , т. е.
, т. е. 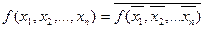 .
.
Из доказанной теоремы следует, что суперпозиция самодвойственных функций самодвойственна, т. е. множество самодвойственных функций образует замкнутый класс.
Замечание: Заметим, что константы являются несамодвойственными функциями.
– Конец работы –
Эта тема принадлежит разделу:
КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОЙ ЛОГИКЕ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ... ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ... имени ВЛАДИМИРА ДАЛЯ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Принцип двойственности.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов