рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Элементы корреляционно-регрессионного анализа
Реферат Курсовая Конспект
Элементы корреляционно-регрессионного анализа
Элементы корреляционно-регрессионного анализа - раздел Математика, Элементы математической статистики В Математическом Анализе Рассматривается Связь Между Величинами, Которую Назы...
В математическом анализе рассматривается связь между величинами, которую называют функциональной. В этом случае величина  определена вполне значениями
определена вполне значениями  , т.е.
, т.е.  . Функциональная связь может существовать и между случайными величинами. Но между случайными величинами может существовать связь и другого ряда, заключающаяся в том, что одна из них реагирует на изменение другой изменениями своего закона распределения. Такую связь называют стохастической или вероятностной. Таким образом,
. Функциональная связь может существовать и между случайными величинами. Но между случайными величинами может существовать связь и другого ряда, заключающаяся в том, что одна из них реагирует на изменение другой изменениями своего закона распределения. Такую связь называют стохастической или вероятностной. Таким образом,  и
и  связаны вероятностной зависимостью, то зная значение одной случайной величины нельзя точно указать, какое значение примет другая величина, а можно указать только закон ее распределения, зависящий от другой случайной величины.
связаны вероятностной зависимостью, то зная значение одной случайной величины нельзя точно указать, какое значение примет другая величина, а можно указать только закон ее распределения, зависящий от другой случайной величины.
Вероятностная зависимость может быть более или менее тесной; при увеличении степени вероятностной связи она все более и более приближается к функциональную зависимость можно рассматривать как предельный, крайний случай вероятностной зависимости. Другой крайний – полная независимость случайных величин. Между этими двумя «полюсами» находятся все степени вероятностной зависимости – от самой слабой до самой сильной.
Наиболее простым и имеющим важное практическое значение видом вероятностной зависимости является корреляционная зависимость.
Корреляционная зависимость между двумя случайными величинами выражается в том, что на изменения одной случайной величины другая случайная величина реагирует изменениями своего математического ожидания:
 ; (9.36)
; (9.36)
или
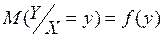 ; (9.37)
; (9.37)
Уравнение (9.36) называют уравнением случайной величины  относительно
относительно  или уравнением регрессии
или уравнением регрессии  на
на  . Соответственно уравнение (9.37) есть уравнение регрессии
. Соответственно уравнение (9.37) есть уравнение регрессии  и
и  .
.
Таким образом, чтобы изучить корреляционную связь, нужно знать условное математическое ожидание случайной величины. В свою очередь для этого необходимо знать аналитический вид двумерного распределения  , котрый зачастую неизвестен. Поэтому идут на упрощение и переходят от условного математического ожидания случайной величины к условному среднему значению, то есть принимают, что:
, котрый зачастую неизвестен. Поэтому идут на упрощение и переходят от условного математического ожидания случайной величины к условному среднему значению, то есть принимают, что:
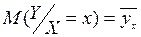 ; (9.38)
; (9.38)
или
 ; (9.39)
; (9.39)
Тогда из формул (9.36) и (9.38) называемое эмпирическое уравнение(эмпирическую функцию) регрессии  на
на  :
:
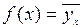 ; (9.40)
; (9.40)
Аналогично из (9.37) и (9.39) имеем эмпирическую функцию регрессии  на
на  :
:
 ; (9.41)
; (9.41)
Вопрос в том, что принять за зависимую переменную, а что за независимую, следует решать применительно к каждому конкретному случаю
При изучении корреляционных связей возникает три основных вопроса: наличие связи, форма связи и сила связи.

Допустим, что проведено  испытаний и при каждом отмечались значения двух случайных величин. В результате получатся
испытаний и при каждом отмечались значения двух случайных величин. В результате получатся  пар выборочных значений
пар выборочных значений  . Для наглядности эти пары значений можно рассматривать как координаты точек на плоскости. Образовавшуюся совокупность точек обычно называют полем корреляции. Поле корреляции дает
. Для наглядности эти пары значений можно рассматривать как координаты точек на плоскости. Образовавшуюся совокупность точек обычно называют полем корреляции. Поле корреляции дает
представление о силе корреляции дает представление о силе корреляцию на рис 8 приведены примеры совокупностей точек, соответствующих сильной (а), слабой (в) корреляции и полному ее отсутствию (с).
Кроме того, по расположению точек на поле корреляции можно в первом приближении сделать предположение о форме и тесноте корреляционной связи.
Пусть сделано предположение о форме корреляционной связи (линенйная, квадратичная, экспоненциальная и т.д.), тем самым можно записать аналитический вид функции 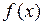 из уравнения (9.40) пока с неопределенными коэффициентами. Для линейной зависимости будем иметь:
из уравнения (9.40) пока с неопределенными коэффициентами. Для линейной зависимости будем иметь:
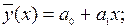 (9.42)
(9.42)
Для квадратичной зависимости:
 (9.43)
(9.43)
Для экспоненциальной зависимости:
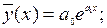 (9.44)
(9.44)
Для обратно пропорциональной зависимости:
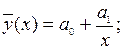 (9.45)
(9.45)
Во всех уравнениях (9.42) – (9.45)  - коэффициенты регрессии;
- коэффициенты регрессии;  - независимая случайная переменная.
- независимая случайная переменная.
Неизвестные коэффициенты регрессии находят, исходя из принципа наименьших квадратов. Согласно епринципу наименьших кавадратов, наилучшее уравнение приближенной регрессии дает та функция из рассматриваемого класса (линейных, квадратичных ит.д.) функций, для которой сумма квадратов:
 ; (9.46)
; (9.46)
Имеет наименьшее значение. В формуле (9.46) функция 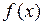 записана со всеми неопределенными коэффициентами
записана со всеми неопределенными коэффициентами  ,…;
,…;  - измеренное значение
- измеренное значение  .
.
Величину S теперь можно рассматривать как функцию от этих неопределенных коэффициентов. Задача состоит в том, чтобы найти набор коэффициентов  ,…, минимизирующий величину S. В математической статистике, как правило, рассматриваются функции
,…, минимизирующий величину S. В математической статистике, как правило, рассматриваются функции 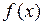 , дифференцируемые по всем своим коэффициентам. При этом условии отыскание минимизирующего набора коэффициентов превращается в несложную задачу математического анализа. Как известно, необходимым условием минимума дифференцируемой функции многих переменных
, дифференцируемые по всем своим коэффициентам. При этом условии отыскание минимизирующего набора коэффициентов превращается в несложную задачу математического анализа. Как известно, необходимым условием минимума дифференцируемой функции многих переменных 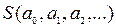 является выполнение равенств:
является выполнение равенств: 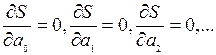 эти равенства можно рассматриватькак уравнения относительно
эти равенства можно рассматриватькак уравнения относительно  ,…; в математической статистике они называются нормальными уравнениями. Так как
,…; в математической статистике они называются нормальными уравнениями. Так как  при любых
при любых  ,…; то у нее обязательно должен существовать хотя бы один минимум. Поэтому если система нормальных уравнений имеетенное решение, то оно и является минимальным для величины S.
,…; то у нее обязательно должен существовать хотя бы один минимум. Поэтому если система нормальных уравнений имеетенное решение, то оно и является минимальным для величины S.
Используя правила дифференцирования, получим систему нормальных уравнений:



……………………….
или
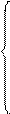


…………………………….
Покажем, как составляются нормальные уравнения для случая линейной регрессии (9.42). отметим, что линейная форма связи занимает особое место в теории корреляции. Можно показать, что линейная регрессия обуславливается двумерным нормальным законом распределения пары случайных величин  .Уравнение (9.46) для случая линейной формы связи между случайными переменными приобретает вид:
.Уравнение (9.46) для случая линейной формы связи между случайными переменными приобретает вид:
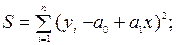
Согласно вышеизложенному алгоритму получение системы нормальных уравнений, находим частные производные функции S по a0 и a1 и приравниваем их к нулю.
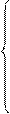 |


После небольших преобразований получим:
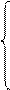
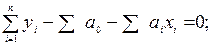
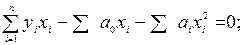
Величины а0 и а1 являются постоянными, поэтому их можно вынести за знак суммы;  есть не что иное, как
есть не что иное, как  . В результате имеем:
. В результате имеем:
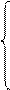

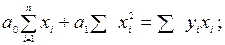 (9.47)
(9.47)
Решая систему нормальных уравнений (9.47), получим значения коэффициентов регрессии:
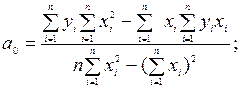 (9.48)
(9.48)
 (9.49)
(9.49)
Получим систему нормальных уравнений для уравнения регрессии вида (9.43) согласно (9.46) имеем:
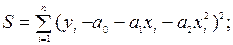
 |
В этом случае
 поэтому система нормальных уравнений имеет вид:
поэтому система нормальных уравнений имеет вид:
 |
или
Полученная система линейна относительно неизвестных коэффициентов  , и ее нетрудно решить, пользуясь известными методами, например, по формулам Крамера или методом Гаусса.
, и ее нетрудно решить, пользуясь известными методами, например, по формулам Крамера или методом Гаусса.
Для уравнения регрессии вида (9.45) согласно (9.46) имеем:  ,
,
Дифференцируя последнее равенство по  и
и  получим:
получим:
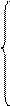
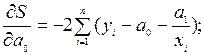

Приравниваем каждое из уравнений нулю, получим следующую систему нормальных уравнений:
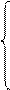
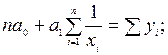

Эта система относительно неизвестных  и
и  также линейна.
также линейна.
Для суждения о степени тесноты связи между случайными величинами чаще всего используют коэффициент корреляции 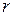 или корреляционное отношение
или корреляционное отношение  . Возможность измерения тесноты связи между случайными величинами с помощью коэффициента корреляции и корреляционного отношения следует из свойств этих показателей, приведенных ниже:
. Возможность измерения тесноты связи между случайными величинами с помощью коэффициента корреляции и корреляционного отношения следует из свойств этих показателей, приведенных ниже:
1. Если коэффициент корреляции  , то x и y связаны точной прямолинейной связью вида:
, то x и y связаны точной прямолинейной связью вида:  или
или 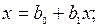
2. Если 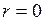 между
между  и
и  не существует прямолинейной корреляционной связи, но криволинейная возможна.
не существует прямолинейной корреляционной связи, но криволинейная возможна.
3. Чем ближе 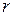 к ±1, тем точнее прямолинейная корреляционная связь между
к ±1, тем точнее прямолинейная корреляционная связь между  и
и  . Она ослабевает с приближением
. Она ослабевает с приближением 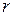 к 0.
к 0.
4. если корреляционное отношение  , то между
, то между  и
и  нет корреляционной связи.
нет корреляционной связи.
5. Если 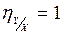 , то
, то  связано с
связано с  однозначной связью, то есть всякому значению
однозначной связью, то есть всякому значению  соответствует одно определенное значение
соответствует одно определенное значение  (функциональная связь).
(функциональная связь).
6. Чем ближе 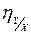 к единице, тем теснее связь между
к единице, тем теснее связь между  и
и  ; чем ближе
; чем ближе 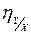 к нулю, тем слабее эта связь.
к нулю, тем слабее эта связь.
7. Если  , то регрессия
, то регрессия  по
по  точно линейна и обратно: если регрессия
точно линейна и обратно: если регрессия  по
по  точно линейна, то
точно линейна, то  .
.
Оценка 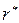 коэффициента корреляции по выборке может быть найдена по формуле:
коэффициента корреляции по выборке может быть найдена по формуле: 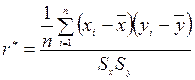 ; (9.50)
; (9.50)
или
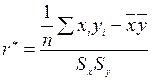 ; (9.51)
; (9.51)
Где  ,
, 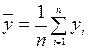 - средние всех наблюдений
- средние всех наблюдений  и
и  ;
; 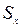 ,
,  - выборочные средние квадратические отклонения случайных величин
- выборочные средние квадратические отклонения случайных величин  и
и  соответственно.
соответственно.
При малом числе наблюдений 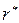 удобно вычислять по формуле:
удобно вычислять по формуле:
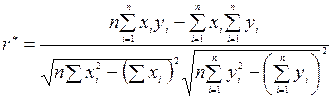 ; (9.52)
; (9.52)
Отметим, что если коэффициент корреляции положительный, то связь между переменными положительная. Это значит, что с ростом значений  увеличивается
увеличивается  . Если коэффициент корреляции имеет отрицательное значение, то связь между переменными отрицательная, то есть с ростом значений
. Если коэффициент корреляции имеет отрицательное значение, то связь между переменными отрицательная, то есть с ростом значений  величина
величина  уменьшается.
уменьшается.
Если коэффициент корреляции равен 0, то говорят, что случайные величины некоррелированы. Некоррелированность не следует смешивать с независимостью, независимые случайные величины некоррелированы. Однако обратное утверждение неверно: некоррелированные случайные величины могут быть зависимы и даже функционально.
При отклонении исследуемой зависимости от линейного вида коэффициент корреляции 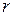 теряет свой смысл как характеристика степени тесноты связи. Более надежной характеристикой при этом оказывается корреляционное отношение
теряет свой смысл как характеристика степени тесноты связи. Более надежной характеристикой при этом оказывается корреляционное отношение 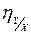 , интерпретация которого не зависит от вида исследуемой зависимости. Выборочное корреляционное отношение
, интерпретация которого не зависит от вида исследуемой зависимости. Выборочное корреляционное отношение  вычисляется по формуле:
вычисляется по формуле:
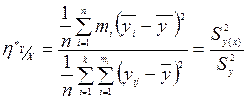 ; (9.53)
; (9.53)
Где числитель  характеризует рассеяние частных средних
характеризует рассеяние частных средних  около своего общего среднего
около своего общего среднего  , а знаменатель – дисперсия
, а знаменатель – дисперсия 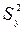 индивидуальных результатов наблюдений относительно общего среднего
индивидуальных результатов наблюдений относительно общего среднего 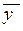 . Аналогично определяется выборочное значение
. Аналогично определяется выборочное значение  .
.
В отличии от коэффициента корреляции корреляционное отношение несимметрично по отношению к исследуемым переменным, то есть  ≠
≠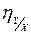 . Отметим, что между
. Отметим, что между  и
и 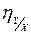 нет какой-либо простой зависимости. Некоррелированность Y с X (то есть равенство нулю величины
нет какой-либо простой зависимости. Некоррелированность Y с X (то есть равенство нулю величины 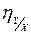 ) не влечет за собой непосредственно некоррелированность Y с X.
) не влечет за собой непосредственно некоррелированность Y с X.
Величина  -
- 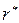 используется в качестве отклонения зависимости от линейной, т.к. обычно
используется в качестве отклонения зависимости от линейной, т.к. обычно  >
> ,
, 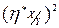 >
> и лишь в случае линейной зависимости
и лишь в случае линейной зависимости  =
= =
=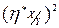 .
.
Замечание. Из теории вероятностей известно, что характеристикой связи (линейной) между случайными величинами Y и X служит коэффициент корреляции:
 ;
;
где 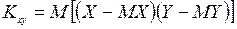 -корреляционный момент,
-корреляционный момент, 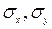 -средние квадратические отклонения случайных величин Y и X соответственно
-средние квадратические отклонения случайных величин Y и X соответственно
Тогда очевидно, что числитель в формуле (9.50) есть оценка корреляционного мотента (см. 9.6), т.е. выборочный корреляционный момент  . Для небольших выборок рекомендуется использовать несмещенную оценку:
. Для небольших выборок рекомендуется использовать несмещенную оценку:
 ; (9.54)
; (9.54)
а выборочные средние квадратические отклонения случайных величин Y и X вычислять ле (9.8).
Числитель в формуле (9.50) достаточно просто преобразуется к выражению в числителе формулы (9.51). Чаще используется формула (9.51) для вычисления величины 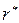 , поэтому для получения несмещенной оценки выборочного корреляционного момента, стоящего в числителе формулы (9.51), рекомендуется вычисленный числитель умножить на
, поэтому для получения несмещенной оценки выборочного корреляционного момента, стоящего в числителе формулы (9.51), рекомендуется вычисленный числитель умножить на 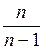 ; величины
; величины 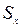 и
и  определить по формуле (9.8).
определить по формуле (9.8).
При корреляционном анализе необходимо оценить достоверность связи между переменными, то есть выяснить, не объясняется ли величина коэффициента корреляции, полученная по выборочным данным, случайностями выборки. Для этого оценивается значимость (существенность) коэффициента корреляции. Проверяется гипотеза Н0 о том, что 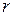 =0, альтернативной является гипотеза Н1 при
=0, альтернативной является гипотеза Н1 при 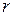 ≠0.
≠0.
В случае совместной нормальной распределенности исследуемых переменных и при достаточно большом объеме выборки  распределение
распределение 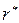 можно считать приближенно нормальным со средним, равным своему теоретическому значению
можно считать приближенно нормальным со средним, равным своему теоретическому значению 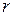 , и дисперсией
, и дисперсией  . Оценка для
. Оценка для  вычисляется по формуле:
вычисляется по формуле:
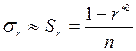 ; (9.55)
; (9.55)
Можно доказать, что в указанной ситуации величина  имеет приближенно нормальное распределение с математическим ожиданием, равным нулю, и дисперсией равной единице. Поэтому проверка значимости (или существенности) коэффициента корреляции сводится к следующему: вычисляется значение
имеет приближенно нормальное распределение с математическим ожиданием, равным нулю, и дисперсией равной единице. Поэтому проверка значимости (или существенности) коэффициента корреляции сводится к следующему: вычисляется значение 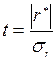 , которое затем сравнивается с найденным по табл. 2. Приложение для заданной вероятности
, которое затем сравнивается с найденным по табл. 2. Приложение для заданной вероятности 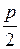 значением
значением  .
.
Если 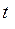 <
< , то принимается гипотеза Н0, то есть коэффициент корреляции считать существенным нельзя и его отклонение от нуля обусловлено неизбежными случайными колебаниями выборки. Если
, то принимается гипотеза Н0, то есть коэффициент корреляции считать существенным нельзя и его отклонение от нуля обусловлено неизбежными случайными колебаниями выборки. Если 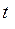 >
> , то гипотеза Н0 отвергается и коэффициент корреляции можно считать существенными, а связь между случайными величинами Y и X достоверной.
, то гипотеза Н0 отвергается и коэффициент корреляции можно считать существенными, а связь между случайными величинами Y и X достоверной.
Однако следует учитывать, что при малых значениях  и значениях
и значениях 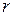 , близких
, близких  ±, это приближение оказывается очень грубым.
±, это приближение оказывается очень грубым.
Пример 6. Результаты наблюдений случайной величины (X; Y) представлены в табл. 9.
Таблица 9
| YX | mj | ||||||
| mi |
Необходимо:
1) вычислить групповые средние 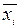 и
и  и построить по ним ломаные эмпирических линию регрессии; 2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
и построить по ним ломаные эмпирических линию регрессии; 2) предполагая, что между переменными X и Y существует линейная корреляционная зависимость:
а) найти уравнение прямых регрессий и построить их графики на том же чертеже, на котором изображены ломаные по групповым средним;
б) вычислить коэффициент корреляции, на уровне значимости  оценить его существенность и сделать вывод о тесноте и направлении связи;
оценить его существенность и сделать вывод о тесноте и направлении связи;
в) используя соответствующее уравнение регрессии, определить среднее значение величины Y для 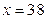 .
.
Пояснения к табл. 9: в последнем столбце таблицы представлены частоты mjпоявлений значений 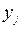 ,
, 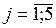 ; в последней строке таблицы представлены частоты miпоявление значений
; в последней строке таблицы представлены частоты miпоявление значений  ,
, 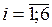 ; на пересечении строк и столбцов представлены частоты
; на пересечении строк и столбцов представлены частоты 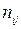 появлений пары
появлений пары 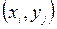 . Объем выборки, как видно из таблицы,
. Объем выборки, как видно из таблицы, 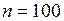 .
.
1) Вычисляем групповые средние 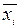 и
и  .
.
Для x = 20: 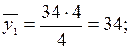 для x = 25:
для x = 25:  для x = 30:
для x = 30: 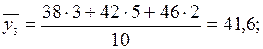 для x = 35:
для x = 35: 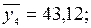 для x = 40:
для x = 40:  для x = 45:
для x = 45: 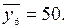
Составляем таблицу:

| ||||||

| 36,86 | 41,6 | 43,12 | 46,42 |
На рис. 9 представлена ломаная эмпирической линии регрессии Y по X. Так как объем выборки велик, то эта ломаная более наглядно представляет тенденцию изменения значений Y при изменении значений X, чем корреляционное поле.
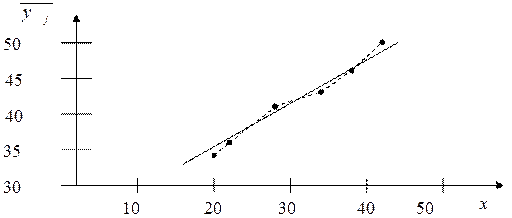 |
Рис. 9 «Ломаная» линия регрессии по групповым средним; график уравнения регрессии Y по X.
По виду ломаной можно предположить наличие линейной корреляционной зависимости между переменными X и Y.
2) Уравнение регрессии ищем в виде  Коэффициенты
Коэффициенты  найдем из системы нормальных уравнений. С учетом частностей появления значений переменных систем (9.47) принимает вид.
найдем из системы нормальных уравнений. С учетом частностей появления значений переменных систем (9.47) принимает вид.
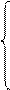

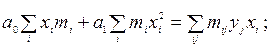
Составляем расчетную таблицу для определения коэффициентов при неизвестных  в системе нормальных уравнений.
в системе нормальных уравнений.
Таблица 9
| YX | mj | yjmi | yi2mi | 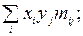
| ||||||
| mi | ||||||||||
| ximi | ||||||||||
| xi2mi |
Пояснение к табл. 9:

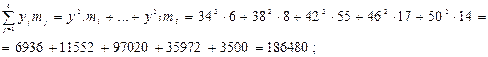


Для первой строчки последнего столбца: 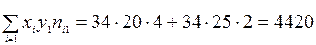 ; аналогично для строк со второй по пятую включительно:
; аналогично для строк со второй по пятую включительно: 
Подставляя данные из табл. 9 в систему нормальных уравнений получим:


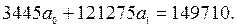
Решая эту систему, находим  тогда уравнение регрессии Y по X имеет вид:
тогда уравнение регрессии Y по X имеет вид:
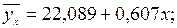 (9.56)
(9.56)
Строим график этой прямой по двум точкам:
При 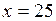
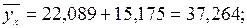
При 

Уравнение регрессии (9.56) дает возможность прогнозировать значение среднее переменной Y в предположении, что независимая переменная X примет определенное значение. Например, для  из уравнения (9.56) получим
из уравнения (9.56) получим 
Данные, приведенные в табл. 9, позволяет определить уравнение регрессии X и Y.
Находим аналогично предыдущему групповые средние:
для y = 34: 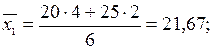 для y = 38:
для y = 38:  для y = 42:
для y = 42: 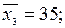 для y = 46:
для y = 46: 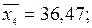 для y = 50:
для y = 50: 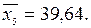 Составляем таблицу:
Составляем таблицу:

| |||||
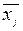
| 21,67 | 26,87 | 36,47 | 39,64 |
 |
Строим ломаную эмпирической линии прогрессии (рис. 10).
 |
Рис. 10 Ломаная линии регрессии по групповым средним; график уравнения регрессии X и Y
Уравнение регрессии для зависимости  ищем в виде:
ищем в виде:  .
.
Система нормальных уравнений имеет вид:
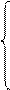
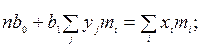
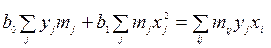 .
.
Исследуя данные таблицы, имеем:

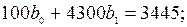
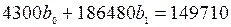 .
.
Решая систему, получаем 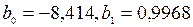 уравнение регрессии X по Y принимает вид:
уравнение регрессии X по Y принимает вид:  .
.
График этой функции строим по двум точкам:
При 

При 
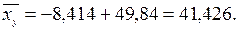
3) Коэффициент корреляции удобно вычислить по формуле (9.52), так все необходимые суммы получены в расчетной табл. 9:
При 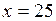
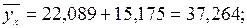
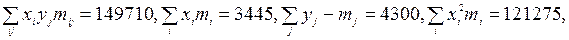
 тогда
тогда  .
.
По формуле (9.55) найдем оценку среднеквадратического отклонения коэффициента корреляции:
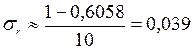 .
.
Зададимся доверительной вероятностью  (уровень значимости
(уровень значимости 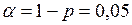 ), и по табл. 2. приложения найдем значение
), и по табл. 2. приложения найдем значение  :
:  Вычисляем величину
Вычисляем величину 
Величина  >>
>> (знак «>>» означает «значительно больше»), поэтому можно сделать вывод о том, что корреляционная зависимость. Так как
(знак «>>» означает «значительно больше»), поэтому можно сделать вывод о том, что корреляционная зависимость. Так как  то есть достаточно близок единицы, то эта зависимость может считаться вполне достаточно тесной; положительный знак коэффициента корреляции указывает на прямо пропорциональную зависимость, то есть с возрастанием значений, например, X значения Y также будут возрастать. Графики уравнений регрессии также подтверждают этот вывод.
то есть достаточно близок единицы, то эта зависимость может считаться вполне достаточно тесной; положительный знак коэффициента корреляции указывает на прямо пропорциональную зависимость, то есть с возрастанием значений, например, X значения Y также будут возрастать. Графики уравнений регрессии также подтверждают этот вывод.
При наибольшем объеме выборки (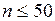 ) величина выборочного коэффициента корреляции
) величина выборочного коэффициента корреляции  считается значимо отличной от нуля, если выполняется неравенство:
считается значимо отличной от нуля, если выполняется неравенство:
 >
>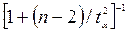
Где 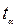 есть критическое значение
есть критическое значение 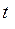 -распределение Стьюдента с
-распределение Стьюдента с 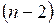 степенями свободы, соответствующее выбранному уровню значимости
степенями свободы, соответствующее выбранному уровню значимости 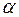 . Поэтому для проверки значимости выборочного коэффициента корреляцтии вычисляется величина:
. Поэтому для проверки значимости выборочного коэффициента корреляцтии вычисляется величина:
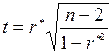 ; (9.57)
; (9.57)
Для проверки нулевой гипотезы находят по табл. 6 распределения Стьюдента по фиксированному уровню значимости 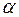 и числу степеней свободы
и числу степеней свободы 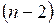 критическое значение
критическое значение 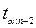 , удовлетворяющее условию
, удовлетворяющее условию  . Если для
. Если для 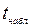 (значения
(значения 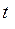 ), вычисленного по формуле (9.57) выполняется
), вычисленного по формуле (9.57) выполняется  , то нулевую гипотезу об отсутствии линейной зависимости между переменными X и Y следует отвергнуть. Если же
, то нулевую гипотезу об отсутствии линейной зависимости между переменными X и Y следует отвергнуть. Если же 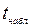 <
<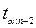 , то нет оснований отвергать нулевую гипотезу о некоррелированности переменных X и Y.
, то нет оснований отвергать нулевую гипотезу о некоррелированности переменных X и Y.
Если же известно, что  , то необходимо воспользоваться Z-преобразованием Фишера (независящим от
, то необходимо воспользоваться Z-преобразованием Фишера (независящим от 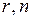 ):
):

Все вышеприведенные рассуждения и формулы, если подходить достаточно строго, справедливы в предложении, что двумерное распределение исследуемых переменных (X,Y) в генеральной совокупности предполагается нормальным или близким к нему.
Пример 7. В результате наблюдений получена выборка:
| X | ||||||||||
| Y | 2,8 | 3,5 | 2,4 | 2,1 | 3,4 | 3,2 | 3,6 | 2,5 | 4,1 | 3,3 |
Требуется построить корреляционное поле найти уравнение регрессии, сделать вывод о тесное связи между переменными (показателями) X и Y, оценить ожидаемое среднее значение Y при 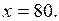
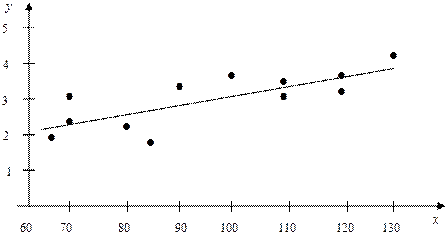
На рис. 10 построено корреляционное поле.
Рис. 10 Корреляционное поле и прямая регрессия
Расположение точек корреляционного поля позволяет высказать предположение о линейном виде корреляционной зависимости между переменными X и Y. Найдем коэффициенты уравнения регрессии 
Составим расчетную табл. 10.
| X | Y | X2 | Y2 | XY |
| 2,8 | 7,84 | |||
| 3,5 | 12,25 | |||
| 2,4 | 5,76 | |||
| 2,1 | 4,41 | 136,5 | ||
| 3,4 | 11,56 | |||
| 3,2 | 10,24 | |||
| 3,6 | 12,96 | |||
| 2,5 | 6,25 | |||
| 4,1 | 16,81 | |||
| 3,3 | 10,89 | |||
| 30,9 | 98,97 | 3077,5 |
В последней строке табл. 10 получены значения: 
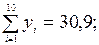
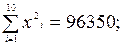


Получим (см (9.47)) систему нормальных уравнений:
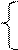

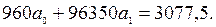
Из которой следует 
 (см. (9.48), (9.49)).
(см. (9.48), (9.49)).
Тогда уравнение регрессии имеет вид:  строим прямую регрессии по точкам: при
строим прямую регрессии по точкам: при 
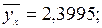

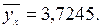
Найдем по формуле (9.50) выборочный коэффициент корреляции  . Предварительно вычислим, учитывая (9.6),
. Предварительно вычислим, учитывая (9.6), 

Используя формулу (7.14), найдем оценки выборочных дисперсий  и
и 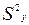 по формуле:
по формуле:
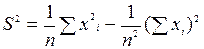
Тогда 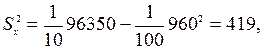 аналогично
аналогично  Выборочный корреляционный момент
Выборочный корреляционный момент  найдем по формуле (9.54):
найдем по формуле (9.54): 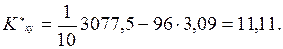
Учитывая что объем выборки небольшой, найдем несмещенные оценки выборочных дисперсий и корреляционного момента, умножив их вычисленные значения на величину: 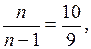 тогда
тогда 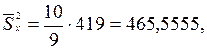

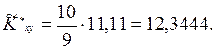 Тогда по формуле (9.50), числитель которой есть выборочный корреляционный момент получим:
Тогда по формуле (9.50), числитель которой есть выборочный корреляционный момент получим: 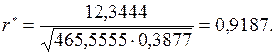
Величина выборочного коэффициента корреляции говорит о достаточно тесной линейной зависимости между переменными X и Y. Те не менее проверим нулевую гипотезу. По формуле (9.57) найдем величину  Зададимся уровнем значимости
Зададимся уровнем значимости  доверительная вероятность
доверительная вероятность  число степеней свободы
число степеней свободы 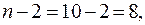 и по табл. 6 находим критическое значение
и по табл. 6 находим критическое значение  Поскольку
Поскольку 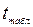 >
> , то нулевую гипотезу об отсутствии линейной зависимости надо отвергнуть и признать наличие достаточно близкой линейной корреляционной связи между переменными X и Y. Прогноз среднего значения переменной Y при X=80 составит
, то нулевую гипотезу об отсутствии линейной зависимости надо отвергнуть и признать наличие достаточно близкой линейной корреляционной связи между переменными X и Y. Прогноз среднего значения переменной Y при X=80 составит 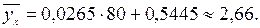
– Конец работы –
Эта тема принадлежит разделу:
Элементы математической статистики
Основные положения Математическую статистику определяют как науку о методах...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Элементы корреляционно-регрессионного анализа
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов