Пространство всех решений однородной системы уравнений. Фундаментальный набор решений однородной системы линейных уравнений.

Теорема 1. Пусть (1) - однородная система линейных уравнений над полем P, U – множество всех решений системы (1), т.е. U=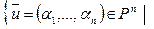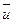- решение системы (1). Тогда множество U является подпространством векторного пространства V=Pⁿ.

Доказательство проводится непосредственной проверкой с помощью критерия подпространства.

Определение 1. Пусть (1) - однородная неопределенная система линейных уравнений над полем P, U – векторное пространство всех решений системы (1). Базис векторного пространства U называется фундаментальным набором решений однородной системы линейных уравнений (1).

Найдём фундаментальный набор решений системы (1). Пусть x_1,…,x_r – главные неизвестные, остальные – свободные неизвестные.

Составим систему векторов из U по следующему правилу (*): придадим первой свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор ; придадим второй свободной неизвестной значение 1, остальным свободным неизвестным – значение 0, получим вектор , и т.д. Получим систему вида:

(2)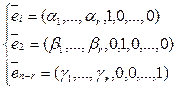. Покажем, что (2) – базис векторного пространства U.

1) Покажем, что система (2) линейно независима. Пусть (3) . Покажем, что 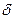_i=0, i=1,. Подставим в (3) значения из (2). Получим

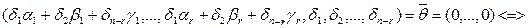
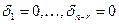. Это означает, что система (2) линейно независима.

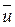2) Покажем, что через векторы системы (2) линейно выражается каждый вектор из U. Пусть . Покажем, что вектор линейно выражается через векторы системы (2). Рассмотрим вектор следующего вида:

Так как (2)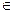U , то 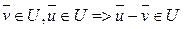. Поскольку 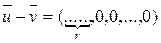и (1) - однородная система линейных уравнений, то => => 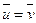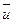линейно выражается через (2).

Из 1) и 2) следует, что система (2) – базис пространства U и, значит, система (2) удовлетворяет определению фундаментального набора решений системы (1).

Вывод: Для того, чтобы найти фундаментальный набор решений однородной системы линейных уравнений, необходимо решить систему методом Гаусса и записать систему 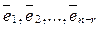по правилу (*).