рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Ядро и образ, ранг и дефект линейного отображения.
Реферат Курсовая Конспект
Ядро и образ, ранг и дефект линейного отображения.
Ядро и образ, ранг и дефект линейного отображения. - раздел Математика, Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства Определение 1. Пусть V И V1 – В...
Определение 1. Пусть V и V1 – векторные пространства над полем Р,  - линейное отображение V в V1. Множество
- линейное отображение V в V1. Множество 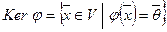 называется ядром линейного отображения j, т.е. ядром линейного отображения j называется множество всех векторов из V, отображающихся при j в нулевой вектор
называется ядром линейного отображения j, т.е. ядром линейного отображения j называется множество всех векторов из V, отображающихся при j в нулевой вектор  .
.
Определение 2. Пусть V и V1 – векторные пространства над полем Р,  - линейное отображение V в V1. Множество
- линейное отображение V в V1. Множество  называется образом линейного отображения j.
называется образом линейного отображения j.
Теорема 1. Пусть V и V1 – векторные пространства над полем Р,  - линейное отображение V в V1. Тогда справедливы следующие утверждения:
- линейное отображение V в V1. Тогда справедливы следующие утверждения:
1) Множество  является подпространством векторного пространства V;
является подпространством векторного пространства V;
2) Множество  является подпространством векторного пространства V1.
является подпространством векторного пространства V1.
Доказательство. 1) Применим к множеству 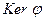 критерий подпространства. Отметим, что так как
критерий подпространства. Отметим, что так как  и
и  , то
, то 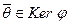 , и значит,
, и значит,  ∅. Кроме того, из определения 2 следует, что
∅. Кроме того, из определения 2 следует, что 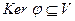 .
.
а) Покажем, что 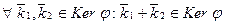 . Действительно, так как
. Действительно, так как 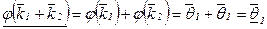 , то
, то  .
.
б) Покажем, что  . Действительно, поскольку
. Действительно, поскольку 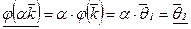 , то
, то  .
.
Из а) и б) по критерию подпространства получаем, что 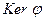 - подпространство векторного пространства V.
- подпространство векторного пространства V.
2) Применим к множеству 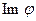 критерий подпространства. Так как
критерий подпространства. Так как  и
и  , то
, то  , и поэтому,
, и поэтому,  ∅. Так как
∅. Так как 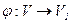 , то из определения 3 следует, что
, то из определения 3 следует, что  .
.
а) Пусть 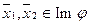 . Покажем, что
. Покажем, что 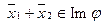 . Так как
. Так как 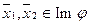 , то по определению 3 существуют такие векторы
, то по определению 3 существуют такие векторы 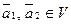 , что
, что 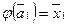 ,
,  . Тогда
. Тогда 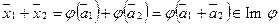 .
.
б) Покажем, что 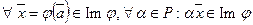 . Действительно,
. Действительно, 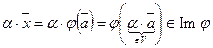 .
.
Из а) и б) по критерию подпространства получаем, что 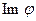 - подпространство векторного пространства V1. Теорема доказана.
- подпространство векторного пространства V1. Теорема доказана.
Определение 3. Пусть V и V1 – конечномерные векторные пространства над полем Р,  - линейное отображение V в V1. Дефектом линейного отображения j называется размерность векторного пространства Kerj, и обозначается d, т.е. d=dimpKerj. Рангом линейного отображения
- линейное отображение V в V1. Дефектом линейного отображения j называется размерность векторного пространства Kerj, и обозначается d, т.е. d=dimpKerj. Рангом линейного отображения 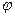 называется размерность векторного пространства
называется размерность векторного пространства 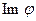 , и обозначается r, т.е. r=dimР
, и обозначается r, т.е. r=dimР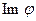 .
.
Теорема 2. Пусть V и V1 – конечномерные векторные пространства над полем Р,  - линейное отображение V в V1, r и d – ранг и дефект линейного отображения j соответственно. Тогда n= r+d.
- линейное отображение V в V1, r и d – ранг и дефект линейного отображения j соответственно. Тогда n= r+d.
25. Линейный оператор. Матрица линейного оператора. Связь между координатными столбцами 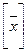 и
и 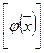
Определение 1. Линейное отображение  называется линейным оператором или эндоморфизмом векторного пространства V.
называется линейным оператором или эндоморфизмом векторного пространства V.
Теорема 1. Пусть V - n-мерное векторное пространство над полем P, 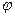 - линейный оператор V. Тогда следующие утверждения равносильны:
- линейный оператор V. Тогда следующие утверждения равносильны:
1) 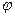 – взаимно-однозначное отображение;
– взаимно-однозначное отображение;
2) Оператор 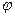 всякий базис пространства V переводит в базис этого пространства;
всякий базис пространства V переводит в базис этого пространства;
3) Оператор 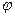 всякую линейно независимую систему векторов из V переводит в линейно независимую систему векторов;
всякую линейно независимую систему векторов из V переводит в линейно независимую систему векторов;
4) Ранг линейного оператора 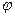 равен n;
равен n;
5) 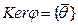 ;
;
Пусть Vn – n-мерное векторное пространство над полем Р,  (1) – базис Vn,
(1) – базис Vn,  . Тогда
. Тогда 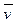 можно разложить по базису (1), т.е.
можно разложить по базису (1), т.е. 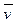 =
=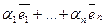 , где
, где 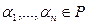 . Введём в рассмотрение две матрицы:
. Введём в рассмотрение две матрицы:
( ) – матрица размера
) – матрица размера 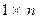 ,
, 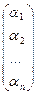 - матрица размера
- матрица размера 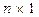 .
.
Матрица 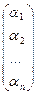 обозначается
обозначается 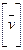 и называется координатным вектором-столбцом вектора
и называется координатным вектором-столбцом вектора  в базисе (1), т.е.
в базисе (1), т.е. 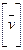 =
=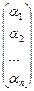 . Тогда (
. Тогда ( 1,…,
1,…, n)·
n)·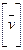 =(
=( 1,…,
1,…, n)·
n)·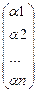 =
= . Таким образом,
. Таким образом, 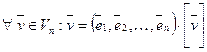 (2).
(2).
Пусть Vn – n-мерное векторное пространство над полем Р,  (1) – базис Vn, j – линейный оператор Vn. Тогда по теореме 3 линейный оператор
(1) – базис Vn, j – линейный оператор Vn. Тогда по теореме 3 линейный оператор 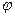 однозначно определяется заданием векторов
однозначно определяется заданием векторов 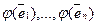 . Так как j: Vn
. Так как j: Vn 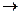 Vn, то
Vn, то  . Поскольку (1) – базис Vn, то вектор
. Поскольку (1) – базис Vn, то вектор  можно разложить по базису (1), i=
можно разложить по базису (1), i=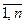 :
:
(3) , т.е.
, т.е.  =
=  , i=
, i=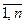 .
.
Определение 2. Пусть Vn – n-мерное векторное пространство над полем Р,  (1) – базис Vn, j – линейный оператор Vn. Матрицей линейного оператора
(1) – базис Vn, j – линейный оператор Vn. Матрицей линейного оператора 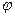 в базисе (1) называется матрица n-го порядка над полем Р, i-ым столбцом которой является координатный вектор-столбец вектора
в базисе (1) называется матрица n-го порядка над полем Р, i-ым столбцом которой является координатный вектор-столбец вектора  в базисе (1), i=
в базисе (1), i=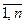 , и обозначается Аφ, т.е.
, и обозначается Аφ, т.е.
Аφ = .
.
Из определения 2 следует, что система (3) может быть записана в матричной форме: 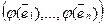 =
=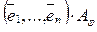 (3′).
(3′).
Действительно,
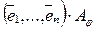 =
=
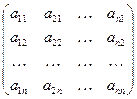 =
=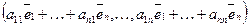 =
=  .
.
Заметим, что между множеством Mn(P) всех матриц n-го порядка над полем Р и множеством всех линейных операторов n-мерного векторного пространства Vn над полем Р существует взаимно однозначное соответствие.
Теорема 2. Пусть 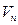 - n-мерное векторное пространство над полем Р,
- n-мерное векторное пространство над полем Р,  (1) – базис Vn,
(1) – базис Vn, 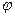 – линейный оператор Vn,
– линейный оператор Vn, 
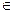
 , А – матрица линейного оператора
, А – матрица линейного оператора 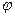 в базисе (1). Тогда
в базисе (1). Тогда  =
=  (4).
(4).
Доказательство. Так как 
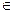 Vn и (1) – базис Vn, то
Vn и (1) – базис Vn, то 
С другой стороны, так как 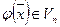 , то по (2)
, то по (2) 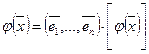 . Следовательно,
. Следовательно,
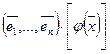 =
=  . Поскольку коэффициенты в базисе (1) определяются однозначно, то последнее равенство означает, что
. Поскольку коэффициенты в базисе (1) определяются однозначно, то последнее равенство означает, что 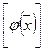 =
= 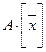 . Теорема доказана.
. Теорема доказана.
– Конец работы –
Эта тема принадлежит разделу:
Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства
Определение Матрицей размера m times n над полем Р называется прямоугольная таблица состоящая из n строк и m столбцов следующего вида... где aij P i j... Определение Квадратной матрицей n го порядка над полем P называется матрица размера n times n над полем P...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Ядро и образ, ранг и дефект линейного отображения.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов