Системы линейных уравнений (СЛУ). Решение системы линейных уравнений. Элементарные преобразования СЛУ. Элементарные преобразования матрицы.

Определение 1. Система линейных уравнений вида (1) , где , 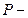поле, называется системой m линейных уравнений с n неизвестными 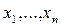над полем 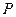, - коэффициенты при неизвестных, 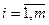, , 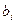- свободные члены системы (1).

Определение 2. Упорядоченная n-ка (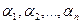), где 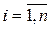, называется решением системы линейных уравнений (1), если при замене переменной 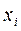на 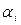каждое уравнение системы (1) превращается в верное числовое равенство.

Определение 3. Система линейных уравнений (1) называется совместной, если она имеет хотя бы одно решение. В противном случае система (1) называется несовместной.

Определение 4. Система линейных уравнений (1) называется определенной, если она имеет единственное решение. В противном случае система (1) называется неопределенной.

Система линейных уравнений

(есть решение) (нет решений)

совместная несовместная

(единственное решение) (не единственное решение)

определеннаянеопределенная

Определение 5. Система линейных уравнений над полем Р называется однородной, если все ее свободные члены равны нулю. В противном случае система называется неоднородной.

Рассмотрим систему линейных уравнений (1). Тогда однородная система вида 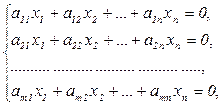называется однородной системой, ассоциированной с системой (1). Однородная СЛУ всегда совместна, так как всегда имеет решение .

Для каждой СЛУ можно ввести в рассмотрение две матрицы - основную и расширенную.

Определение 6. Основной матрицей системы линейных уравнений (1) называется матрица, составленная из коэффициентов при неизвестных следующего вида: .

Определение 7. Расширенной матрицей системы линейных уравнений (1) называется матрица , полученная из матрицы путем присоединения к ней столбца свободных членов: .

Определение 8. Элементарными преобразованиями системы линейных уравнений называются следующие: 1) умножение обеих частей некоторого уравнения системы на скаляр ; 2) прибавление к обеим частям одного уравнения системы соответствующих частей другого уравнения, умноженных на элемент 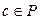; 3) добавление или отбрасывание уравнения вида .

Определение 9. Две системы линейных уравнений над полем Р относительно переменных 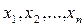называются равносильными, если их множества решений совпадают.

Теорема 1. Если одна система линейных уравнений получена из другой с помощью элементарных преобразований, то такие системы равносильны.

Удобно элементарные преобразования применять не к системе линейных уравнений, а к ее расширенной матрице.

Определение 10. Пусть дана матрица с элементами из поля Р. Элементарными преобразованиями матрицы называются следующие:

1) умножение всех элементов какой-либо строки на матрицы на aÎ Р^#;

2) умножение всех элементов какой-либо строки на матрицы на aÎ Р^# и сложение с соответствующими элементами другой строки;

3) перестановка местами любых двух строк матрицы;

4) добавление или вычёркивание нулевой строки.

8. Решение СЛУ: метод последовательного исключения неизвестных (метод Гаусса).

Рассмотрим один из основных методов решения систем линейных уравнений, который называется методом последовательного исключения неизвестных, или иначе, методом Гаусса. Рассмотрим систему (1) m линейных уравнений с n неизвестными над полем Р: (1) .

В системе (1) хотя бы один из коэффициентов 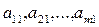при не равен 0. В противном случае (1) - система уравнений с (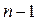) неизвестными - это противоречит условию. Поменяем местами уравнения так, чтобы коэффициент при 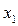в первом уравнении был не равен 0. Таким образом, можно считать, что . Умножим обе части первого уравнения на и прибавим к соответствующим частям второго, третьего, …, m-го уравнений соответственно. Получим систему вида: 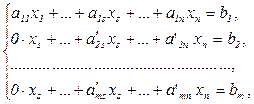, где s - наименьшее число, такое что хотя бы один из коэффициентов при не равен 0. Поменяем местами уравнения так, чтобы во второй строке коэффициент при переменной был не равен 0, т.е. можем считать, что 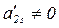. Тогда умножим обе части второго уравнения на и прибавим к соответствующим частям третьего, …, m-го уравнений соответственно. Продолжая этот процесс, получим систему вида: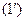

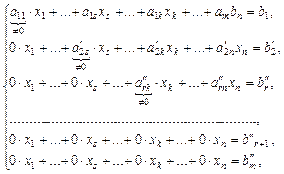
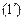- система линейных уравнений, которая, согласно теореме 1, равносильна системе (1). Система 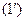называется ступенчатой системой линейных уравнений. Возможны два случая: 1) Хотя бы один из элементов не равен 0. Пусть, например, 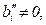. Тогда в системе линейных уравнений 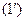есть уравнение вида , что невозможно. Это означает, что система 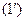не имеет решений, и поэтому система (1) не имеет решений (в этом случае (1) - несовместная система).

2) Пусть ,…, . Тогда с помощью элементарного преобразования З) получим систему 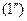- систему r линейных уравнений с n неизвестными. При этом переменные при коэффициентах 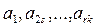называются главными переменными (это 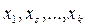), их всего r. Остальные (n-r) переменных называют свободными.

Возможны два случая: 1) Если r=n, то 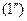- система треугольного вида. В этом случае из последнего уравнения находим переменную , из предпоследнего - переменную ,…, из первого уравнения - переменную 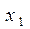. Таким образом, получаем единственное решение системы линейных уравнений 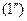, а значит, и системы линейных уравнений (1) (в этом случае система (1) определена).

2) Пусть r<n. В этом случае главные переменные выражают через свободные и получают общее решение системы линейных уравнений (1). Придавая свободным переменным произвольные значения, получают различные частные решения системы линейных уравнений (1) (в этом случае система (1) неопределена).

При решении системы линейных уравнений методом Гаусса элементарные преобразования удобно производить не над системой, а над её расширенной матрицей.

Определение. Рангом матрицы А называется число ненулевых строк любой ступенчатой матрицы, к которой приводится А элементарными преобразованиями. Ранг матрицы А обозначается через r(A) или rang(A).

Алгоритм решения системы линейных уравнений методом Гаусса

1. Составить расширенную матрицу системы линейных уравнений (1) и с помощью элементарных преобразований привести к ступенчатому виду.

2. Провести исследование: а) если , то система (1) несовместна;

б) если 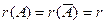, то система (1) совместна.

При этом если r=n, то система (1) определена, если r<n, то система (1) неопределена.

3. Найти решение системы, соответствующей полученной ступенчатой матрице.