рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Простейшие свойства векторного пространства

Реферат Курсовая Конспект

Выберите учебное заведение

Простейшие свойства векторного пространства

Простейшие свойства векторного пространства - раздел Математика, Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства Пусть V — Векторное Пространство Над Полем Р. Тогда Справедливы Следующие Сво...

Пусть V — векторное пространство над полем Р. Тогда справедливы следующие свойства.

Свойство 1. Для любого из V 0×= , где 0 — ноль поля Р, — нулевой элемент аддитивной группы V, т. е. ноль-вектор.

Доказательство. 0×= (0 + 0) = А₄ = 0×+ 0×, т.е. 0×= 0×+ 0×(1)

С другой стороны 0×= 0×+ (2)

Из (1) и (2) 0×+ = 0×+ 0×. В илу закона сокращения в аддитивной группе V, получим 0×= . Свойство доказано.

Свойство 2. Для любого a из Р a×=.

Доказательство. a×=a×(+ )= А₃ = a×+ a×(3)

a×= a×+ (4)

Из (3) и (4) a×+ = a×+ a×. Проводя левостороннее сокращение, из последнего равенства получим a×= . Свойство доказано.

Свойство 3. Если a= (5), то либо a=0 либо = .

Доказательство. Если a = 0, то требуемое равенство верно. Если a ¹ 0, то существует a^-1 Î Р. Умножим обе части равенства (5) слева на a^-1. Получим a^-1(a) = a^-1, откуда, по А₂ и свойству 2,

(a^-1a) = Û 1×= Û (по А₅) = . Свойство доказано.

Свойство 4. Для любого из V выполняется -1×= -.

Доказательство. = (свойство 1)= 0×= (1+(-1)) = А₄ = 1×+ (-1)× = А₅ = + (-1)× . Прибавим к обеим частям последнего равенства слева -. Получим (-1)×= -. Свойство доказано.

Следствие 1. Для любого a из Р, для любого из V выполняется (-a)= -a .

Следствие 2. Для любых a и b из Р, для любого из V выполняется (a - b)= a - b .

Свойство 5. Для любого a из Р, для любых , , 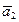…, 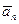из V выполняется

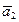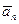a(+ + … + ) = a+ a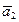+ … + a.

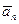Свойство 6. Для любых a₁, a₂, … , a_n из Р, для любого из V выполняется

(a₁ + a₂ + … + a_n) = a₁+ a₂+ … + a_n.

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства

Определение Матрицей размера m times n над полем Р называется прямоугольная таблица состоящая из n строк и m столбцов следующего вида... где aij P i j... Определение Квадратной матрицей n го порядка над полем P называется матрица размера n times n над полем P...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Простейшие свойства векторного пространства

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Умножение матрицы на скаляр, транспонирование матриц, умножение матриц и их основные свойства.
Определение 1. Пусть A=(aij) – матрица размера m×n над полем P,

Разложение определителя по ряду. Минор и алгебраическое дополнение к элементу определителя. Связь алгебраических дополнений с минорами.
Пусть Δ = =

Системы линейных уравнений (СЛУ). Решение системы линейных уравнений. Элементарные преобразования СЛУ. Элементарные преобразования матрицы.
Определение 1. Система линейных уравнений вида (1) , где

Формула для вычисления обратной матрицы.
Теорема 1. Пусть A=- матрица n-го порядка над полем P. Е

Формулы Крамера.
Теорема 1. Пусть (1) - система n линейных уравнений с n неизвестн

Линейная комбинация системы векторов. Линейно зависимая и линейно независимая системы векторов.
Определение 1. Пусть V – векторное пространство над полем P и ,

Свойства линейно зависимой системы векторов.
Рассмотрим некоторые свойства линейно зависимой системы векторов. Свойство 1. Система векторов, содержащая линейно зависимую подсистему, является линейно зависимой.

Базис системы векторов. Координаты вектора в данном базисе. Разложение вектора по базису — существование и единственность.
Пусть дана система векторов (1) ,

Изоморфизм векторных пространств одинаковой размерности.
Определение. Пусть V1 и V2 — векторные пространства над одним и тем же полем P. Говорят, что V1 изоморфно V2 (обозначается V

Пространство всех решений однородной системы уравнений. Фундаментальный набор решений однородной системы линейных уравнений.
Теорема 1. Пусть (1) - однородная система линейных уравнений над полем P, U – множеств

Связь между решениями неоднородной системы линейных уравнений с решениями ассоциированной с ней однородной системы линейных уравнений.
Лемма 1. Пусть (1) - неоднородная система линейных уравнений над полем P, (2)

Линейная оболочка системы векторов. Размерность подпространства. Размерность суммы двух подпространств.
Определение 1. Пусть V - векторное пространство над полем Р, —.система в

Матрица перехода от базиса к базису. Преобразование координат.
Пусть Vn - n-мерное векторное пространство над полем P, (1) – базис Vn

Ядро и образ, ранг и дефект линейного отображения.
Определение 1. Пусть V и V1 – векторные пространства над полем Р,