рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Линейная комбинация системы векторов. Линейно зависимая и линейно независимая системы векторов.
Реферат Курсовая Конспект
Линейная комбинация системы векторов. Линейно зависимая и линейно независимая системы векторов.
Линейная комбинация системы векторов. Линейно зависимая и линейно независимая системы векторов. - раздел Математика, Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства Определение 1. Пусть V – Векторное Пространство Над Полем P ...
Определение 1. Пусть V – векторное пространство над полем P и  ,
, 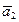 , …,
, …, 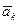 (1) – система векторов из V. Любая часть системы векторов (1) называется подсистемой системы векторов (1).
(1) – система векторов из V. Любая часть системы векторов (1) называется подсистемой системы векторов (1).
Определение 2. Вектор 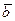 ÎV называется линейной комбинацией системы векторов (1), если существуют скаляры a1, a2,..., aк Î P такие, что
ÎV называется линейной комбинацией системы векторов (1), если существуют скаляры a1, a2,..., aк Î P такие, что 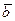 = a1
= a1 + a2
+ a2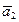 + … + ak
+ … + ak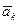 .
.
Определение 3. Система векторов называется линейно зависимой, если по крайней мере один из векторов этой системы является линейной комбинацией остальных векторов системы. Система векторов называется линейно независимой, если ни один из векторов этой системы не является линейной комбинацией остальных векторов системы.
Теорема.Система векторов (1) является линейно зависимой тогда и только тогда, когда существуют скаляры a1, a2,..., aк Î P, не равные нулю одновременно, такие, что
a1 + a2
+ a2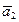 + … + ak
+ … + ak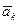 =
= (2)
(2)
Доказательство. Необходимость. Пусть система векторов (1) линейно зависима. Тогда по определению хотя бы один из векторов системы (1) является линейной комбинацией остальных векторов системы. Пусть, например,  является линейной комбинацией остальных векторов, то есть существуют скаляры a2,..., aк Î P такие, что
является линейной комбинацией остальных векторов, то есть существуют скаляры a2,..., aк Î P такие, что  = a2
= a2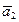 + a3
+ a3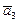 + … + ak
+ … + ak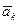 (3). Перенося в равенстве (3) все векторы в левую часть, получим
(3). Перенося в равенстве (3) все векторы в левую часть, получим  - a2
- a2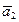 - a3
- a3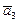 - … - ak
- … - ak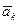 =
= . Таким образом, выполняется равенство (2), в котором a1= 1 ¹ 0.
. Таким образом, выполняется равенство (2), в котором a1= 1 ¹ 0.
Достаточность. Пусть выполняется равенство (2) в котором скаляры a1, a2,..., aк Î P одновременно не равны нулю. Пусть a1 ¹ 0. Тогда из равенства (2) получим a1 = - a2
= - a2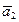 - a3
- a3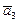 - … - ak
- … - ak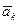 . Следовательно, умножая обе части последнего равенства на (a1)-1Î Р, получим
. Следовательно, умножая обе части последнего равенства на (a1)-1Î Р, получим
 = -
= -
 -
- 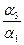
 - … -
- … - 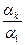
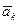 . Так как
. Так как  ,
, 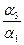 , … ,
, … , 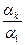 Î Р, то
Î Р, то  является линейной комбинацией остальных векторов системы (1). Поэтому система векторов (1) линейно зависима по определению. Теорема доказана.
является линейной комбинацией остальных векторов системы (1). Поэтому система векторов (1) линейно зависима по определению. Теорема доказана.
Следствие. Система векторов (1) является линейно независимой, если из равенства (2) следует a1=a2=...=aк=0.
Замечание. Неверно, что любой вектор линейно зависимой системы линейно выражается через остальные. Пусть, например,  — произвольный ненулевой вектор. Система {
— произвольный ненулевой вектор. Система { ,
,  } линейно зависима, так как 0×
} линейно зависима, так как 0× + 1×
+ 1× =
=  , но очевидно, что вектор
, но очевидно, что вектор  линейно не выражается через ноль-вектор.
линейно не выражается через ноль-вектор.
– Конец работы –
Эта тема принадлежит разделу:
Матрицы. Основные определения – прямоугольная, квадратная, диагональная, треугольная, нулевая и единичная матрицы. Сложение матриц и его свойства
Определение Матрицей размера m times n над полем Р называется прямоугольная таблица состоящая из n строк и m столбцов следующего вида... где aij P i j... Определение Квадратной матрицей n го порядка над полем P называется матрица размера n times n над полем P...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Линейная комбинация системы векторов. Линейно зависимая и линейно независимая системы векторов.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов