рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Вид работы: Методические Указания
- /
- МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Реферат Курсовая Конспект
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ - Методические Указания, раздел Математика, Н.л. Гамершмид, Г.в. Прусакова ...
Н.Л. ГАМЕРШМИД, Г.В. ПРУСАКОВА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
Для студентов-заочников
инженерных специальностей АГАУ
БАРНАУЛ 2008
МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «АЛТАЙСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
Н.Л. Гамершмид, Г.В. Прусакова
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
И КОНТРОЛЬНЫЕ ЗАДАНИЯ
ПО ВЫСШЕЙ МАТЕМАТИКЕ
Для студентов-заочников инженерных специальностей АГАУОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Порядок выполнения контрольных работ На первом курсе обучения студенты-заочники выполняют работы 1 и 2; на втором – 3 и 4.После получения работы (как зачтенной, так и незачтенной) студент должен исправить в ней все отмеченные рецензентом недостатки. В случае незачета студент обязан в кратчайший срок выполнить все требования рецензента и представить работу на повторное рецензирование, приложив при этом первоначально выполненную работу.
4. В период экзаменационной сессии студент обязан представить все прорецензированные и зачтенные контрольные работы. При необходимости студент должен давать на экзамене устные пояснения ко всем или некоторым задачам, содержащимся в этих работах.
5. Студент выполняет тот вариант контрольных работ, который совпадает с последней цифрой его учебного шифра (номер зачетной книжки). При этом если предпоследняя цифра учебного шифра есть число нечетное (1, 3, 5, 7, 9), то номера задач для соответствующего варианта даны в таблице 1 (6 стр. данного пособия), для студентов, обучающихся по сокращенной программе, номера задач для соответствующего варианта даны в таблице 3 (8 стр. данного пособия); если же предпоследняя цифра учебного шифра есть число четное или ноль (2, 4, 6, 8, 0), то номера задач для соответствующего варианта даны в таблице 2 (7 стр. пособия), . для студентов, обучающихся по сокращенной программе, номера задач для соответствующего варианта даны в таблице 4 (8 стр. данного пособия).
6. Если в процессе изучения материала или при решении той или иной задачи у студента возникают вопросы, на которые он не может ответить сам, то ему следует обратиться к ведущему преподавателю для получения консультации.
ТАБЛИЦЫ ВАРИАНТОВ
Таблица 1
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||||||
| Работа 1 | Работа 2 | |||||||||||||||||||
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||||||
| Работа 3 | Работа 4 | |||||||||||||||||||
Таблица 2
| Номер варианта | Номера задач для контрольных работ | ||||||||||||||||||
| Работа 1 | Работа 2 | ||||||||||||||||||
| Номер варианта | Номера задач для контрольных работ | ||||||||||||||||||
| Работа 3 | Работа 4 | ||||||||||||||||||
Таблица 3
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||
| Работа 1 | Работа 2 | |||||||||||||||
Таблица 4
| Номер варианта | Номера задач для контрольных работ | |||||||||||||||
| Работа 1 | Работа 2 | |||||||||||||||
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ
Тема 1. Элементы аналитической геометрии на плоскости
Ефимов, гл. 1-4. Минорский, № 61, 62, 77, 78, 82 (1-3), 86-88, 95, 96, 126-129, 135, 136. Разберите решение задачи 1 из данного пособия.
Ефимов, гл. 5, 6. Минорский, № 140, 144, 155, 166, 169, 170, 180, 189, 190, 204, 206, 211, 212, 214, 226. Разберите решение задач 1, 2, 3, 4 из данного пособия.
Примеры решения задач
Задача 1.Даны координаты вершин треугольника АВС: А(4; 3), В(16;-6), С(20; 16). Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты СD и ее длину; 5) уравнение медианы AE и координаты точки К пересечения этой медианы с высотой CD; 6) уравнение прямой, проходящей через точку К параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой СD.
Решение:
1. Расстояние d между точками A(x1,y1) и B(x2,y2) определяется по формуле
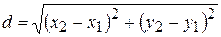 (1)
(1)
Применяя (1), находим длину стороны АВ:
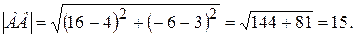
2. Уравнение прямой, проходящей через точки A(x1,y1) и B(x2,y2) имеет вид
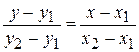 (2)
(2)
Подставляя в (2) координаты точек А и В, получим уравнение стороны АВ:

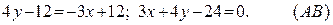
Решив последнее уравнение относительно у, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:
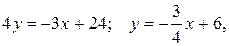 откуда
откуда 
Подставив в (2) координаты точек В и С, получим уравнение прямой ВС:
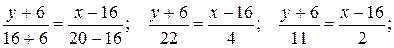
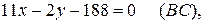 или
или 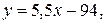
откуда 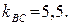
3. Известно, что тангенс угла 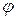 между двумя прямыми, угловые коэффициенты которых соответственно равны
между двумя прямыми, угловые коэффициенты которых соответственно равны  и
и 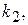 вычисляется по формуле
вычисляется по формуле
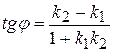 (3)
(3)
Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: 
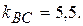 Применяя (3), получим
Применяя (3), получим

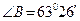 или
или 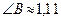 рад.
рад.
4. Уравнение прямой, проходящей через данную точку в заданном направлении, имеет вид
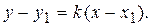 (4)
(4)
Высота CD перпендикулярна стороне АВ. Чтобы найти угловой коэффициент высоты CD, воспользуемся условием перпендикулярности прямых. Так как 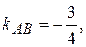 то
то 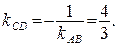 Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим
Подставив в (4) координаты точки С и найденный угловой коэффициент высоты, получим

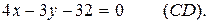
Чтобы найти длину высоты CD, определим сначала координаты точки D— точки пересечения прямых АВ и CD. Решая совместно систему:
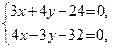 находим
находим 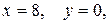 т.е. D(8;0).
т.е. D(8;0).
По формуле (1) находим длину высоты CD:
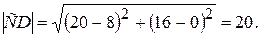
5. Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
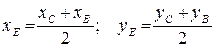 (5)
(5)
Следовательно,

Подставив в (2) координаты точек А и Е, находим уравнение медианы:
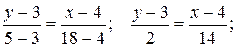
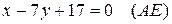
Чтобы найти координаты точки пересечения высоты CD и медианы АЕ, решим совместно систему уравнений
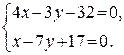 Находим
Находим  .
.
6. Так как искомая прямая параллельна стороне АВ, то ее угловой коэффициент будет равен угловому коэффициенту прямой АВ. Подставив в (4) координаты найденной точки К и угловой коэффициент 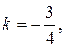 получим
получим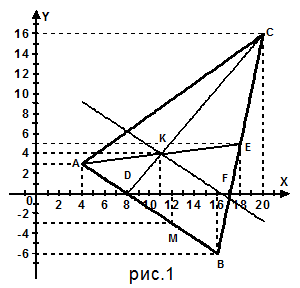

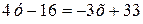
3x + 4y – 49 = 0 (KF)
7. Так как прямая АВ перпендикулярна прямой CD, то искомая точка М, расположенная симметрично точке А относительно прямой CD, лежит на прямой АВ. Кроме того, точка D является серединой отрезка AM. Применяя формулы (5), находим координаты искомой точки М:

Треугольник ABC, высота CD, медиана АЕ, прямая KF и точка М построены в системе координат хОу на рис. 1.
Задача 2.Составить уравнение геометрического места точек, отношение расстояний которых до данной точки А(4; 0) и до данной прямой х=1 равно 2. 
Решение:
В системе координат хОу построим точку А(4;0) и прямую х = 1. Пусть М(х;у) – произвольная точка искомого геометрического места точек. Опустим перпендикуляр MB на данную прямую x = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1. Ордината точки В равна ординате точки М. Следовательно, В(1;у) (рис. 2).
По условию задачи |МА|: |МВ| = 2. Расстояния |МА| и |MB| находим по формуле (1) задачи 1:

Возведя в квадрат левую и правую части, получим
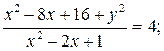
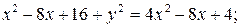
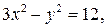 или
или 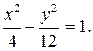
Полученное уравнение представляет собой гиперболу, у которой действительная полуось а = 2, а мнимая – 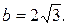
Определим фокусы гиперболы. Для гиперболы выполняется равенство  Следовательно,
Следовательно, 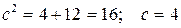 и
и  – фокусы гиперболы. Как видно, заданная точка А(4;0) является правым фокусом гиперболы.
– фокусы гиперболы. Как видно, заданная точка А(4;0) является правым фокусом гиперболы.
Определим эксцентриситет полученной гиперболы:

Уравнения асимптот гиперболы имеют вид 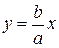 и
и 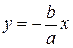 . Следовательно,
. Следовательно,  или
или  и
и  – асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.
– асимптоты гиперболы. Прежде чем построить гиперболу, строим ее асимптоты.
Задача 3. Составить уравнение геометрического места точек, равноудаленных от точки А(4; 3) и прямой у = 1. Полученное уравнение привести к простейшему виду.
Решение: Пусть М(х; у) — одна из точек искомого геометрического места точек. Опустим из точки М перпендикуляр MB на данную прямую у = 1 (рис. 3). Определим координаты точки В. Очевидно, что абсцисса точки В равна абсциссе точки М, а ордината точки В равна 1, т. е. В(х; 1). По условию задачи |МА|=|МВ|. Следовательно, для любой точки М(х;у), принадлежащей искомому геометрическому месту точек, справедливо равенство:
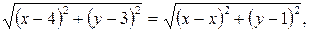 или
или 

Полученное уравнение определяет параболу с вершиной в точке 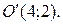 Чтобы уравнение параболы привести к простейшему виду, положим
Чтобы уравнение параболы привести к простейшему виду, положим 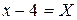 и y + 2 = Y тогда уравнение параболы принимает вид:
и y + 2 = Y тогда уравнение параболы принимает вид: 

Чтобы построить найденную кривую, перенесем начало координат в точку О'(4;2), построим новую систему координат 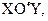 оси которой соответственно параллельны осям Ox и Oy и затем в этой новой системе построим параболу (*) (рис. 3).
оси которой соответственно параллельны осям Ox и Oy и затем в этой новой системе построим параболу (*) (рис. 3).
Задача 4.Составить каноническое уравнение гиперболы, фокусы которой расположены на оси абсцисс, если она проходит через точки A(-8;12) и B(12;8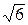 ). Найти все точки пересечения этой гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы.
). Найти все точки пересечения этой гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы.
Решение: Каноническое уравнение гиперболы имеет вид
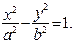 (1)
(1)
По условию точки А и В лежат на гиперболе. Следовательно, координаты этих точек удовлетворяют уравнению (1). Подставив в уравнение (1) вместо текущих координат х и у координаты точек А и В, получим систему двух уравнений относительно неизвестных а и b:
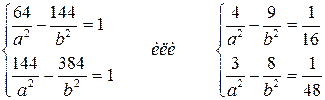
Решая систему, получаем: 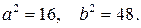 Таким образом, уравнение искомой гиперболы
Таким образом, уравнение искомой гиперболы 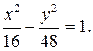 Определим фокусы этой гиперболы. Имеем
Определим фокусы этой гиперболы. Имеем  тогда
тогда 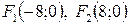 .
.
Уравнение окружности, проходящей через начало координат, имеет вид x2 + y2 = R2
 где R — радиус окружности. Так как по условию окружность проходит через фокусы гиперболы, то R = с = 8. Следовательно, x2 + y2 = 64 — уравнение окружности. Чтобы найти точки пересечения гиперболы с окружностью, решим систему уравнений
где R — радиус окружности. Так как по условию окружность проходит через фокусы гиперболы, то R = с = 8. Следовательно, x2 + y2 = 64 — уравнение окружности. Чтобы найти точки пересечения гиперболы с окружностью, решим систему уравнений 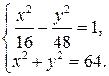
В результате получим 4 точки пересечения: 

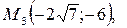
 (рис. 4).
(рис. 4).
Тема 2. Основы векторной алгебры
Задача 5.Даны координаты вершин пирамиды ABCD: A(2;1;0), B(3;-1;2), C(13;3;10), D(0;1;4). Требуется: 1) записать векторы и в системе орт и найти… Решение: 1. Произвольный вектор может быть представлен в системе орт следующей формулой:Тема 3. Элементы аналитической геометрии в пространстве
Задача 6. Даны координаты четырех точек: А (0; -2; -1), B(2; 4; -2), С(3; 2; 0) и М(-11; 8; 10). Требуется: 1) составить уравнение плоскости Q,… Решение: 1) Уравнение плоскости, проходящей через три данные точки имеет вид … (1)Тема 4. Элементы линейной алгебры
Задача 8. Решить систему линейных уравнений: а)методом Гаусса; б) с помощью определителей; в) с помощью обратной матрицы.Тема 5. Введение в анализ
Пискунов, гл. 1, § 1—9, упр. 1—9, 39, 40; гл. II, § 1—5, упр. 1—6, 9—29; § 6—8, упр. 31—35, 38, 41—48; § 9—10, упр. 57, 59; § 11, упр. 60—62.
Разберите решения задач 10—12 из данного пособия.
Задача 10. Найти указанные пределы:
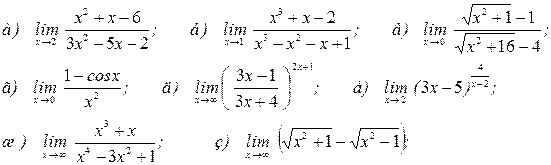
Решение: а) Непосредственная подстановка предельного значения аргумента  приводит к неопределенности вида 0/0, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель
приводит к неопределенности вида 0/0, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель 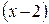 . Так как аргумент
. Так как аргумент  только стремиться к своему предельному значению 2, но не совпадает с ним, то множитель
только стремиться к своему предельному значению 2, но не совпадает с ним, то множитель 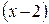 отличен от нуля при
отличен от нуля при 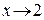 :
:
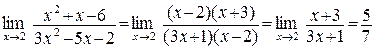 .
.
б) Непосредственная подстановка предельного значения аргумента 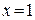 приводит к неопределенности вида 0/0, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель
приводит к неопределенности вида 0/0, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель на множители и сократим члены дроби на общий множитель  . Так как аргумент
. Так как аргумент  только стремиться к своему предельному значению 1, но не совпадает с ним, то множитель
только стремиться к своему предельному значению 1, но не совпадает с ним, то множитель  отличен от нуля при
отличен от нуля при  :
:
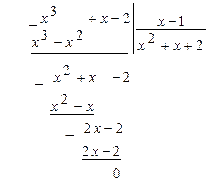
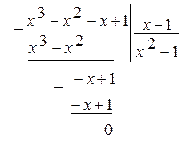
Имеем:

в) Непосредственная подстановка предельного значения аргумента  приводит к неопределенности вида 0/0, чтобы раскрыть эту неопределенность, домножим числитель и знаменатель на сопряжённые выражения для числителя и знаменателя (чтобы применить формулу
приводит к неопределенности вида 0/0, чтобы раскрыть эту неопределенность, домножим числитель и знаменатель на сопряжённые выражения для числителя и знаменателя (чтобы применить формулу  ).
).
Тогда 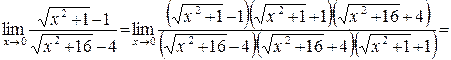
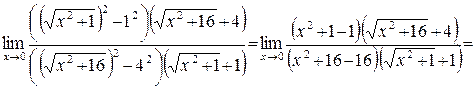
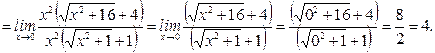
г)  .
.
Использовали первый замечательный предел  .
.
Искомый предел можно найти иначе. Известно, что при нахождении предела отношения двух бесконечно малых величин можно каждую из них (или только одну) заменить другой бесконечно малой, ей эквивалентной, так при  ~
~ , то
, то
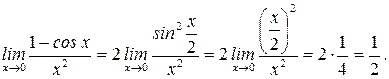
д) при 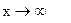 основание степени
основание степени  стремится к 1, а показатель степени
стремится к 1, а показатель степени  стремится к бесконечности. Следовательно, имеем неопределенность вида
стремится к бесконечности. Следовательно, имеем неопределенность вида 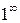 . Представим основание в виде суммы 1 и некоторой бесконечно малой величины:
. Представим основание в виде суммы 1 и некоторой бесконечно малой величины:

Тогда

Положим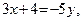 при
при  переменная
переменная 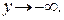 Выразим показатель степени через новую переменную у. Так как 3х = –5у – 4, то
Выразим показатель степени через новую переменную у. Так как 3х = –5у – 4, то
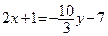 . Таким образом,
. Таким образом,
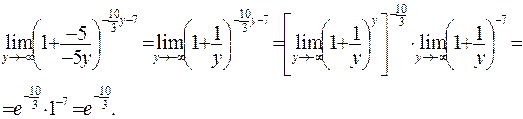
(используем второй замечательный предел).
Другой способ.
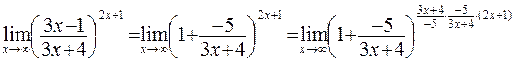 =
=
=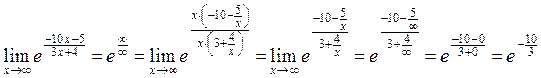 .
.
е) При 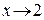 основание (3х–5) стремится к единице, а показатель степени
основание (3х–5) стремится к единице, а показатель степени 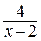 стремится к бесконечности.
стремится к бесконечности.
Положим 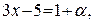 где
где 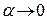 при
при  Тогда
Тогда 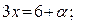
 и
и 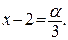
Выразив основание и показатель степени через 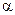 , получим
, получим

ж) Непосредственная подстановка предельного значения аргумента приводит к неопределенности вида 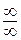 . Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на
. Чтобы раскрыть эту неопределенность, разделим числитель и знаменатель на 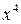 .
.

Другой способ: вынесем в числителе и знаменателе за скобки старшие степени x.

з) Непосредственная подстановка предельного значения аргумента приводит к неопределенности вида  . Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сопряженное выражение, чтобы применить формулу a2–b2=(a–b)(a+b).
. Чтобы раскрыть эту неопределенность, умножим числитель и знаменатель дроби на сопряженное выражение, чтобы применить формулу a2–b2=(a–b)(a+b).


Задача 11.Дана функция 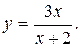
Требуется: 1) установить, является ли данная функция непрерывной или разрывной при значениях аргумента  и
и 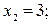 2) найти односторонние пределы в точках разрыва; 3) построить график данной функции на отрезке [–6; 6].
2) найти односторонние пределы в точках разрыва; 3) построить график данной функции на отрезке [–6; 6].
Решение: 1) Если ищется предел функции у = f(x) при условии, что аргумент х, стремясь к своему предельному значению а, может принимать только такие значения, которые меньше а, то этот предел, если он существует, называется левосторонним (левым) пределом данной функции в точке х = а и условно обозначается так:

Если ищется предел функции у = f(x) при условии, что аргумент х, стремясь к своему предельному значению а, может принимать только такие значения, которые больше а, то этот предел, если он существует, называется правосторонним (правым) пределом данной функции в точке х = а и условно обозначается так:

Функция у = f(x) непрерывна при х = а, если выполняются следующие условия:
1) функция у = f(x) определена не только в точке а, но и в некотором интервале, содержащем эту точку;
2) функция у = f(x) имеет при 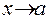 конечные и равные между собой односторонние пределы;
конечные и равные между собой односторонние пределы;
3) односторонние пределы при 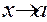 совпадают со значением функции в точке а, т. е.
совпадают со значением функции в точке а, т. е.

Если для данной функции у = f(x) в данной точке х = а хотя бы одно из перечисленных трех условий не выполняется, то функция называется разрывной в точке х = а. 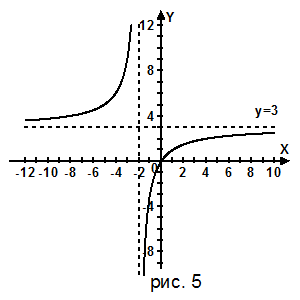
Разрыв функции у = f(x) в точке х = а называется разрывом первого рода, если односторонние пределы слева и справа существуют, но не равны между собой. Если же хотя бы один из односторонних пределов не существует, разрыв в этой точке называется разрывом второго рода.
При х = –2 данная функция не существует: в этой точке функция терпит разрыв. Определим односторонние пределы функции при 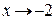 слева и справа
слева и справа

так как знаменатель стремится к нулю, оставаясь отрицательным.
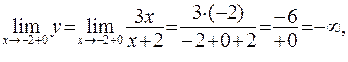
так как знаменатель стремиться к нулю, оставаясь положительным.
Таким образом, при х =–2 данная функция имеет разрыв второго рода.
При х = 3 данная функция непрерывна, так как выполняются все три условия непрерывности функции.

Исследуем поведение функции на концах области определения: 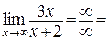

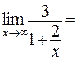
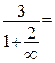
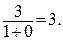
Данная функция является дробно-линейной. Известно, что графиком дробно-линейной функции служит равносторонняя гипербола, асимптоты которой параллельны осям координат (прямоугольных):  и
и  . График функции показан на рис. 6.
. График функции показан на рис. 6.
Задача 12.Функция у задана различными аналитическими выражениями для различных областей изменения аргумента х: 
 Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти предел функции у при приближении аргумента х к точке разрыва слева и справа; 3) найти скачок функции в точке разрыва.
Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти предел функции у при приближении аргумента х к точке разрыва слева и справа; 3) найти скачок функции в точке разрыва.
Решение: Данная функция определена и непрерывна в интервалах 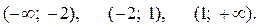
При х = — 2 и х = 1 меняется аналитическое выражение функции, и только в этих точках функция может иметь разрыв.
Определим односторонние пределы в точке х = – 2:
 .
.
Односторонние пределы совпадают. Функция в этой точке непрерывна. Определим односторонние пределы в точке х = 1:
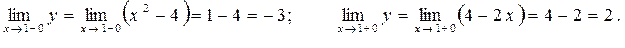
Так как односторонние пределы функции у в точке х = 1 не равны между собой, то в этой точке функция имеет разрыв первого рода.
Скачком функции в точке разрыва называется абсолютная величина разности между ее правым и левым предельными значениями. Следовательно, в точке х=1 скачок функции 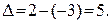 График функции показан на рис. 5.
График функции показан на рис. 5.
Тема 6 Производная и дифференциал
Пискунов, гл. IV, § 1—3, упр. 1—7, 9, 10; § 4—5, упр. 18—30, 34— 36, 38—40; § 6—7, упр. 53—55. Разберите решения задач 13 —17 из данного пособия. Задача 13.Найти производные следующих функций:Тема 7. Исследование поведения функции
Задача 18. Исследовать функцию и построить ее график. Решение: 1. Определим область существования функции. Квадратный трехчлен, стоящий под знаком логарифма, можно представить так:…Тема 8. Неопределенный интеграл
Задача 21.Найти неопределённые интегралы: а) б); в)г) ; д)е); ж); з)и) ; к) ; л) . Решение: При нахождении неопределённых интегралов функций используют следующие свойства:Тема 9. Определенный интеграл
Задача 22.Вычислить интеграл Решение: Сделаем подстановку. ПустьТема 10. Приложения определенного интеграла
Пискунов, гл. XII, § 1—2, упр. 1—4, 6—11, 13—15; § 3, упр. 37, 38, 40—42, 47, 48; § 4—5, упр. 19, 20, 23, 25, 27, 28; § 6, упр. 49—53, 56; § 7—8, упр. 59—62, 64, 65/67, 69, 73. Разберите решение задачи 24 из данного пособия.
Задача 24.Вычислить площадь поверхности эллипсоида, полученного вращением вокруг оси Ох эллипса:
 (1)
(1)
Решение: Площадь поверхности, образованной вращением вокруг оси Ох дуги кривой у = f(x) между точкамис абсциссами х = а и х = b, вычисляется по формуле
 (2)
(2)
Из уравнения эллипса (1) находим 
Производная  Используя формулу (2), получим
Используя формулу (2), получим
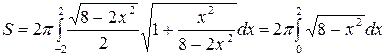
Чтобы вычислить последний интеграл, положим 
Тогда z = 0 при х = 0 и  при х = 2.
при х = 2.

Тема 11. Функции нескольких переменных
Задача 25.Исследовать на экстремум функцию Решение: Чтобы исследовать данную дважды дифференцируемую функцию z = f(x, у)… 1. Найти частные производные первого порядка и приравнять их к нулю и решить систему уравненийТема 12. Кратные интегралы. Криволинейный интеграл.
Задача 28. Дан интеграл Требуется: 1) построить на плоскости хОу область интегрирования D;Тема 13. Ряды и их приложения.
Минорский№2422, 2425, 2432, 2438, 2444, 2470, 2473, 2492, 2525, 2533.
Разберите решения задач 29-31 из данного пособия.
Задача 29.Найти область сходимости степенного ряда  .
.
Решение: Данный степенной ряд можно записать так:

Применяем признак Даламбера:
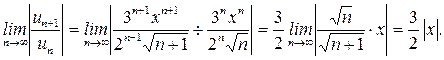
Ряд будет сходиться для тех значений х, для которых 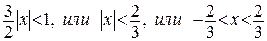 .
.
Определим сходимость на концах интервала. При х= –2/3 ряд примет вид:

Этот ряд является знакочередующимся; его общий член по абсолютному значению стремится к нулю при 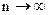 . По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что этот ряд сходится. Следовательно, значение х = - 2/3 принадлежит области сходимости данного ряда.
. По признаку Лейбница о сходимости знакочередующихся рядов заключаем, что этот ряд сходится. Следовательно, значение х = - 2/3 принадлежит области сходимости данного ряда.
Подставив х = 2/3, получим
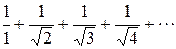
Этот ряд расходится, так как каждый член этого ряда начиная со второго больше соответствующего члена гармонического ряда. Следовательно, значение х = 2/3 не принадлежит области сходимости данного ряда. Таким образом, 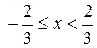 – область сходимости исследуемого ряда.
– область сходимости исследуемого ряда.
Задача 30.Вычислить интеграл 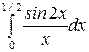 с точностью до 0,001.
с точностью до 0,001.
Решение: Предварительно представим подынтегральную функцию в виде степенного ряда. Используя известное разложение в степенной ряд Маклорена функции sinx, имеем:
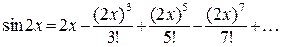 , тогда
, тогда 
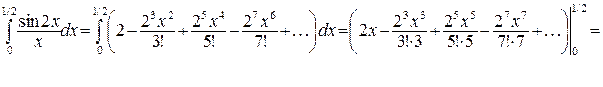
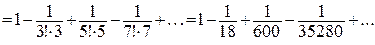
Мы получили знакочередующийся ряд, который удовлетворяет условиям теоремы Лейбница. Так как в полученном ряде четвертый член по абсолютному значению меньше 0,001, то ограничиваемся только первыми тремя членами.
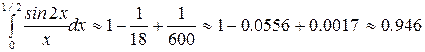
Задача 31. Найти первые три (отличные от нуля) члена разложения в степенной ряд Маклорена функции у(х), являющейся частным решением дифференциального уравнения  если у(0)=1.
если у(0)=1.
Решение: Положим, что у(х) является решением данного дифференциального уравнения при указанных начальных условиях. Если у(х) допускает разложение в ряд Маклорена, то имеем:
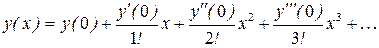 (1)
(1)
Свободный член разложения (1), то есть у(0), дан по условию. Чтобы найти значения 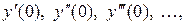 нужно данное уравнение последовательно дифференцировать по переменной х и затем вычислять значения производных при х = 0.
нужно данное уравнение последовательно дифференцировать по переменной х и затем вычислять значения производных при х = 0.
Значение  получаем, подставив начальное условие в дифференциальное уравнение
получаем, подставив начальное условие в дифференциальное уравнение

Подставив найденные значения производных при х = 0 в (1), получим разложение искомого частного решения заданного уравнения:

Ответ: 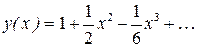
Тема 14. Дифференциальные уравнения первого порядка
Задача 32.Найти общее решение уравнения . Решение: Данное уравнение является однородным, так как коэффициенты при и есть… Если , то дифференциал , и данное уравнение примет вид.
Мы получили уравнение с разделенными переменными относительно 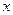 и
и 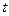 . Интегрируя, находим общее решение этого уравнения:
. Интегрируя, находим общее решение этого уравнения:
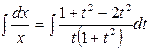 ;
;  ;
;
 ;
;  .
.
Потенцируя, находим  , или
, или 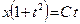 . Из введенной подстановки следует, что
. Из введенной подстановки следует, что 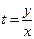 . Следовательно,
. Следовательно, 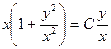
 или
или  – общее решение данного уравнения.
– общее решение данного уравнения.
Задача 33.Найти общее решение уравнения  .
.
Решение: Данное уравнение является линейным, так как оно содержит искомую функцию  и её производную
и её производную 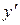 в первой степени и не содержит их произведений.
в первой степени и не содержит их произведений.
Применяем подстановку 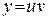 , где
, где 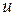 и
и  - некоторые неизвестные функции аргумента
- некоторые неизвестные функции аргумента  . Если
. Если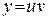 , то
, то  и данное уравнение примет вид
и данное уравнение примет вид
 ,
,
или
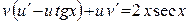 . (1)
. (1)
Так как искомая функция  представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию
представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию 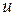 так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т.е. выберем функцию
так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т.е. выберем функцию 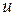 так, чтобы имело место равенство
так, чтобы имело место равенство
 (2)
(2)
При таком выборе функции 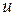 уравнение (1) примет вид
уравнение (1) примет вид
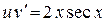 . (3)
. (3)
Уравнение (2) есть уравнение с разделяющимися переменными относительно 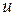 и
и  . Решим это уравнение:
. Решим это уравнение:
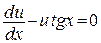 ;
;  ;
;  ;
;
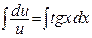 ;
; 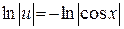 ,
, 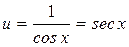 .
.
Чтобы равенство (2) имело место, достаточно найти одно какое – либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С=0. Подставив в (3) найденное выражение для 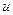 , получим:
, получим:  ;
;  ;
; 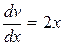 ;
; 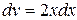 . Интегрируя, получаем
. Интегрируя, получаем 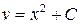 . Тогда
. Тогда  - общее решение данного уравнения.
- общее решение данного уравнения.
Тема 15. Дифференциальные уравнения второго порядка
Задача 34.Дано уравнение: . Найти частное решение, удовлетворяющее начальным условиям: ; . Решение: Данное дифференциальное уравнение второго порядка не содержит явно…Тема 16. Основы теории вероятностей
Задача 38.Всхожесть семян данного растения составляет 90 %. Найти вероятность того, что из пяти посеянных семян взойдут: а) четыре; б) не менее… Решение: Воспользуемся формулой Бернулли. Если производится п независимых… , (1)ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ
В задачах 1—20 даны координаты вершин треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В… 1.A(-7;-2), B(5;-11), C(9;11). 2.A(-4;8), B(8;-1), C(12;21).А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г).
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А); б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
А) ; б) ; в) ; г) .
В задачах 141—150 даны функции y=f(x) и значения аргумента  и
и  . Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3) построить график данной функции.
. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3) построить график данной функции.
141. 
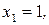

142. 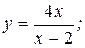


143. 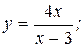

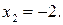
144. 
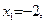

145. 
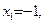

146. 
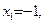
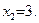
147. 
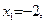

148. 


149. 


150. 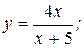
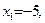

В задачах 151—160функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) определить характер разрыва; 3) сделать рисунок.
151. 

152. 
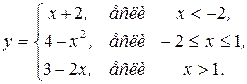
153. 
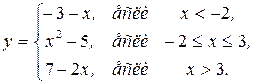
154. 

155. 
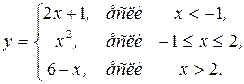
156. 
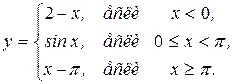
157. 

158. 
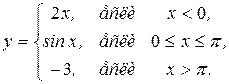
159. 

160.
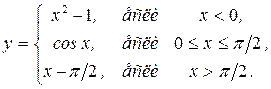
В задачах 161-180 определить производные 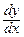 , пользуясь формулами дифференцирования.
, пользуясь формулами дифференцирования.
161.а)  б)
б)  в)
в)  г)
г) 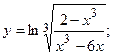 д)
д) 
162.а) 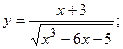 б)
б)  в)
в) 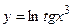 г)
г) 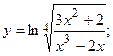 д)
д) 
163.а) 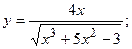 б)
б)  в)
в) 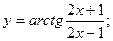 г)
г)  д)
д) 
164.а) 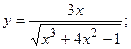 б)
б)  в)
в) 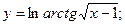 г)
г) 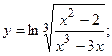 д)
д) 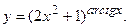
165.а)  б)
б)  в)
в)  г)
г)  д)
д) 
166.а)  б)
б) 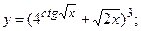 в)
в) 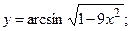 г)
г)  д)
д) 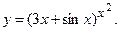
167.а)  б)
б) 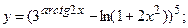 в)
в)  г)
г)  д)
д) 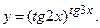
168.а) 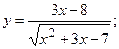 б)
б)  в)
в)  г)
г) 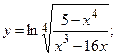 д)
д) 
169.а) 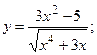 б)
б) 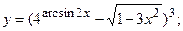 в)
в)  г)
г)  д)
д) 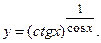
170.а) 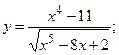 б)
б)  в)
в)  г)
г)  д)
д) 
171.а) 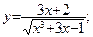 б)
б)  в)
в) 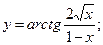 г)
г) 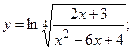 д)
д) 
172.а)  б)
б)  в)
в)  г)
г) 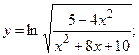 д)
д) 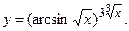
173.а) 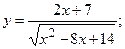 б)
б)  в)
в) 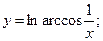 г)
г) 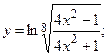 д)
д) 
174.а) 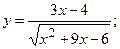 б)
б) 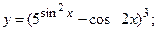 в)
в) 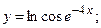 г)
г) 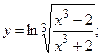 д)
д) 
175.а)  б)
б) 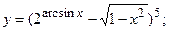 в)
в) 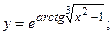 г)
г) 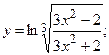 д)
д) 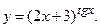
176.а) 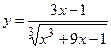 б)
б)  в)
в) 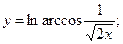 г)
г) 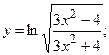 д)
д) 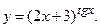
177.а)  ; б)
; б)  в)
в)  ; г)
; г)  д)
д) 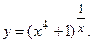
178.а) 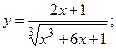 б)
б) 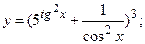 в)
в) 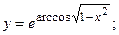 г)
г) 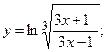 д)
д) 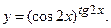
179.а) 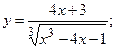 б)
б) 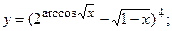 в)
в) 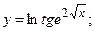 г)
г) 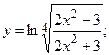 д)
д) 
180.а) 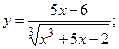 б)
б) 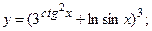 в)
в) 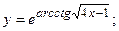 г)
г) 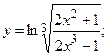 д)
д) 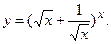
В задачах 181—200 исследовать данные функции методами дифференциального исчисления и начертить их графики. Исследование и построение графика рекомендуется проводить по следующей схеме: 1) найти область существования функции; 2) исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в точках разрыва; 3) выяснить, не является ли данная функция четной, нечетной; 4) найти точки экстремума функции и определить интервалы возрастания и убывания функции; 5) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции; 6) найти асимптоты графика функции, если они имеются; 7) построить график функции, используя результаты исследования; при необходимости можно дополнительно находить точкиграфика, давая аргументу х ряд значений и вычисляя соответствующие значения у.
181. 
182. 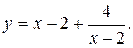
183. 
184. 
185. 
186. 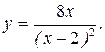
187. 
188. 
189. 
190. 
191. 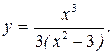
192. 
193. 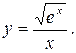
194. 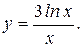
195. 
196. 
197. 
198. 
199. 
200. 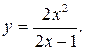
201.Требуется изготовить открытый сверху цилиндрический сосуд максимальной вместимости. Каковы должны быть размеры сосуда (радиус R и высота H), если на его изготовление имеется S=84,82дм2 материала
(S ≈ 27π) ?
202.Требуется вырыть яму конической формы (воронку) с образующей а = 3 м. При какой глубине объем воронки будет наибольшим?
203.Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R?
204.В эллипс 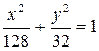 вписать прямоугольник наибольшей площади. Найти стороны этого прямоугольника, если они параллельны осям.
вписать прямоугольник наибольшей площади. Найти стороны этого прямоугольника, если они параллельны осям.
205.Требуется изготовить закрытый цилиндрический бак максимальной вместимости. Каковы должны быть размеры бака (радиус R и высота H), если на его изготовление имеется S = 18,84 м2 материала (S ≈ 6π)?
206.В прямоугольной системе координат через точку М (2; 3) проведена прямая, которая вместе с осями координат образует треугольник, расположенный в первом квадранте. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?
207.Резервуар, открытый сверху, имеет форму прямоугольного параллелепипеда с квадратным основанием. Каковы должны быть размеры резервуара, чтобы на егo изготовление пошло наименьшее количество материала, если он должен вмещать 256 л воды?
208.Требуется вырыть яму цилиндрической формы с круглым основанием и вертикальной боковой поверхностью заданного объема V = 25 м2 (V≈8π). Каковы должны быть линейные размеры ямы (радиус R и высота H), чтобы на облицовку ее дна и боковой поверхности пошло наименьшее количество материала?
209.Из круглого бревна радиуса R = 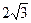 требуется вырезать балку прямоугольного сечения с основанием b и высотой h. Прочность балки пропорциональна bh2. При каких значениях b и h прочность балки будет наибольшей?
требуется вырезать балку прямоугольного сечения с основанием b и высотой h. Прочность балки пропорциональна bh2. При каких значениях b и h прочность балки будет наибольшей?
210.Требуется изготовить закрытый цилиндрический бак заданного объема V= 50м3 (V≈16π). Каковы должны быть размеры бака (радиус R и высота H), чтобы на его изготовление пошло наименьшее количество материала?
211.Турист идет из пункта А, находящегося на шоссейной дороге, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой составляет 17 км. В каком месте туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если его скорость передвижения по шоссе 5 км/ч, а по бездорожью 3 км/ч?
212.Требуется поставить палатку в форме правильной четырехугольной пирамиды заданной боковой поверхности S = 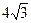 м2. Каковы должны быть размеры палатки (сторона основания а и высота H), чтобы вместимость палатки была наибольшей?
м2. Каковы должны быть размеры палатки (сторона основания а и высота H), чтобы вместимость палатки была наибольшей?
213.Равнобедренный треугольник, периметр которого Р = 12, вращается вокруг основания. Найти основание а, при котором полученное тело вращения имеет наибольший объем?
214.Цистерна имеет форму прямого кругового цилиндра, завершенного с одной стороны полушаром. Вместимость цистерны V=41,89м (V≈
(V≈ π). Найти радиус цилиндра R, при котором цистерна будет иметь наименьшую полную поверхность.
π). Найти радиус цилиндра R, при котором цистерна будет иметь наименьшую полную поверхность.
215.Сечение оросительного канала имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь?
216.Требуется изготовить полотняный шатер, имеющий форму прямого кругового конуса заданной вместимости V=14,14м3 (V≈9/2π). Каковы должны быть размеры конуса (высота H и радиус основания R), чтобы на шатер ушло наименьшее количество полотна?
217.Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения P=35,7м (P≈20+5π). При каком радиусе полукруга площадь сечения будет наибольшей?
218.Из прямоугольного листа жести размером 24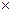 9 см требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была наибольшей?
9 см требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была наибольшей?
219.Равнобедренный треугольник, вписанный в окружность радиуса R= 3, вращается вокруг основания. Найти высоту треугольника h, при котором полученное тело вращения имеет наибольший объем.
220.Найти высоту конуса наибольшего объема, который можно вписать в шар радиуса R.
В задачах 221–240 найти интегралы:
221.а) ; б)
; б) 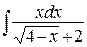 ; в)
; в) .
.
222.а)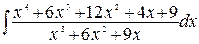 ; б)
; б)  ; в)
; в) 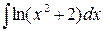 .
.
223.а) 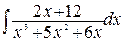 ; б)
; б) 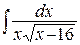 ; в)
; в)  .
.
224.а) 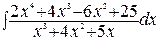 ; б)
; б)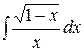 ; в)
; в) 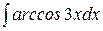 .
.
225.а)  ; б)
; б) 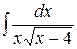 ; в)
; в)  .
.
226.а)  ; б)
; б) 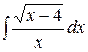 ; в)
; в)  .
.
227.а)  ; б)
; б)  ; в)
; в) 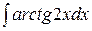 .
.
228.а) 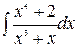 ; б)
; б)  ; в)
; в)  .
.
229.а)  ; б)
; б) 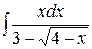 ; в)
; в) 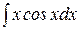 .
.
230.а)  ; б)
; б)  ; в)
; в) 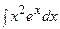 .
.
231.а)  ; б)
; б)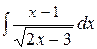 ; в)
; в) 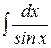 .
.
232.а) 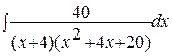 ; б)
; б) 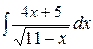 ; в)
; в) 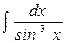 .
.
233.а) 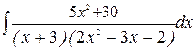 ; б)
; б) 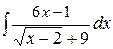 ; в)
; в) 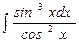 .
.
234.а) 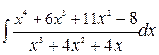 ; б)
; б) ; в)
; в)  .
.
235.а) 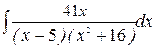 ; б)
; б) 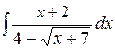 ; в)
; в)  .
.
236.а)  ; б)
; б)  ; в)
; в) 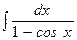 .
.
237.а) 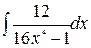 ; б)
; б) ; в)
; в)  .
.
238.а)  ; б)
; б) ; в)
; в) 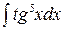 .
.
239.а)  ; б)
; б)  ; в)
; в)  .
.
240.а) 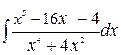 ; б)
; б)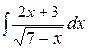 ; в)
; в) 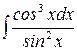 .
.
В задачах 241–260 вычислить определенные интегралы:
241.а) 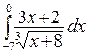 ; б)
; б)  .
.
242.а)  ; б)
; б) 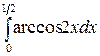 .
.
243.а)  ; б)
; б)  .
.
244.а) 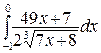 ; б)
; б)  .
.
245.а) 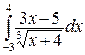 ; б)
; б) 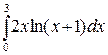 .
.
246.а)  ; б)
; б)  .
.
247.а) 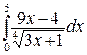 ; б)
; б) 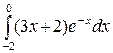 .
.
248.а) 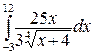 ; б)
; б) 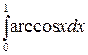 .
.
249.а) 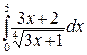 ; б)
; б) 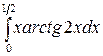 .
.
250.а) 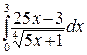 ; б)
; б)  .
.
251.а) 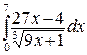 ; б)
; б)  .
.
252.а)  ; б)
; б) 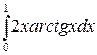 .
.
253.а)  ; б)
; б) 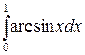 .
.
254.а)  ; б)
; б) 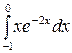 .
.
255.а) 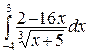 ; б)
; б) 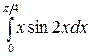 .
.
256.а)  ; б)
; б)  .
.
257.а)  ; б)
; б) 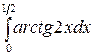 .
.
258.а)  ; б)
; б)  .
.
259.а)  ; б)
; б)  .
.
260.а) 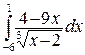 ; б)
; б) 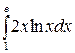 .
.
261..Вычислить площадь фигуры, ограниченной параболами 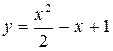 и
и 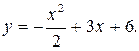
262.Вычислить площадь фигуры, ограниченной эллипсом 

263.Вычислить площадь фигуры, ограниченной астроидой 
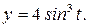
264.Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой  прямой
прямой  и осью Оx.
и осью Оx.
265.Найти объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной гиперболой y=6/x,осью Оу и прямыми у = 1 и у = 6.
266.Найти объем тела, полученного вращением вокруг оси Ох эллипса x=acost, y=bsint.
267.Найти длину дуги кривой  от
от 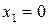 до
до 
268.Найти длину дуги кривой  от
от  до
до 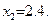
269.Найти длину одной арки циклоиды x=a(t-sint), y=a(1-cost).
270.Найти длину кардиоиды ρ=2a(1-cosφ).
271.Найти площадь поверхности, образованной вращением вокруг оси Ох параболы 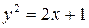 от
от 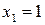 до
до 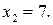
272.Найти площадь поверхности, образованной вращением вокруг оси Ох астроиды 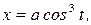
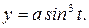
273.Найти площадь поверхности, образованной вращением вокруг оси Ох одной арки циклоиды х = 3(t — sint), у = 3(1 — cos t).
274.Найти площадь фигуры, ограниченной окружностями ρ =асоsφ и ρ =2а соsφ (а > 0).
275.Найти площадь фигуры, ограниченной кардиоидой ρ = 2(1- cosφ) и окружностью ρ = 2.
276.Найти координаты центра тяжести однородной плоской фигуры, ограниченной дугой синусоиды у= sinx и отрезком оси Ох от 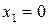 до
до 
277.Найти координаты центра тяжести однородной плоской фигуры, ограниченной кривой  осью Ох и прямой х = 4.
осью Ох и прямой х = 4.
278.Найти координаты центра тяжести однородной плоской фигуры, ограниченной кривой 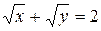 и осями координат.
и осями координат.
279.Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболой и прямой
и прямой 
280.Найти координаты центра тяжести однородной плоской фигуры, ограниченной эллипсом 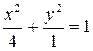 и окружностью
и окружностью 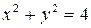 и расположенной в первом квадранте.
и расположенной в первом квадранте.
В задачах 281– 300 вычислить несобственные интегралы или установить их расходимость.
281.
282.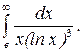
283.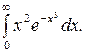
284.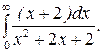
285.
286.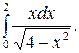
287.
288.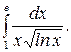
289.
290.
291.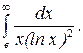
292.
293.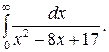
294.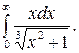
295.
296.
297.
298.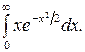
299.
300.
В задачах 301– 310дана функция 
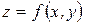 . Найти: 1) полный дифференциал dz;
. Найти: 1) полный дифференциал dz;
2) частные производные второго порядка 
 и
и  ;
;
3) смешанные частные производные  и
и 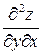 .
.
301. 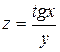 .
.
302. 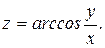
303. 
304. 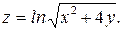
305. 
306. 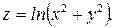
307. 
308. 
309. 
310. .
311.Дана функция  . Показать, что
. Показать, что 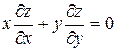
312.Дана функция  . Показать, что
. Показать, что  .
.
313.Дана функция 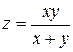 . Показать, что
. Показать, что 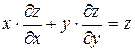 .
.
314.Дана функция  . Показать, что
. Показать, что 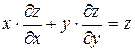 .
.
315.Дана функция  . Показать, что
. Показать, что  .
.
316.Дана функция  . Показать, что
. Показать, что  .
.
317.Дана функция 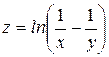 . Показать, что
. Показать, что  .
.
318.Дана функция  . Показать, что
. Показать, что 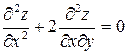 .
.
319.Дана функция 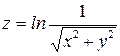 . Показать, что
. Показать, что 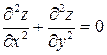 .
.
320.Дана функция 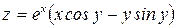 . Показать, что
. Показать, что 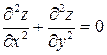 .
.
В задачах 321—330 найти наименьшее и наибольшее значения функции z=f(x, у) в заданной замкнутой области.
321.  в квадрате
в квадрате 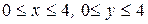 .
.
322.  в треугольнике, ограниченном осями координат Оx и Oy и прямой
в треугольнике, ограниченном осями координат Оx и Oy и прямой  .
.
323.  в квадрате
в квадрате  .
.
324. 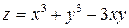 в квадрате
в квадрате 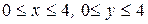 .
.
325. 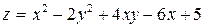 в треугольнике, ограниченном осями координат Оx и Oy и прямой
в треугольнике, ограниченном осями координат Оx и Oy и прямой 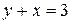
326. 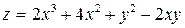 в области, ограниченной параболой
в области, ограниченной параболой 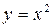 , осью Oy
, осью Oy и прямой
и прямой 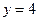 .
.
327.  в прямоугольнике
в прямоугольнике  .
.
328.  в области, ограниченной параболой
в области, ограниченной параболой 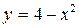 и осью Ox.
и осью Ox.
329.  в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми 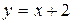 ,
, ,
, .
.
330.  в прямоугольнике
в прямоугольнике 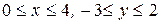 .
.
В задачах 331–340 данную функцию z = f(x, у) исследовать на экстремум.
331. 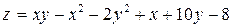 .
.
332.  .
.
333. 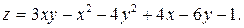
334.  .
.
335. 
336. 
337. 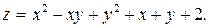
338. 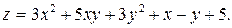
339. 
340. 
В задачах 341–360 требуется: 1) построить на плоскости хОу область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.
341. 
342. 
343. 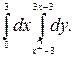
344. 
345. 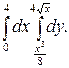
346. 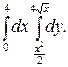
347. 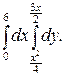
348. 
349. 
350. 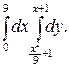
351. 
352. 
353. 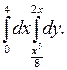
354. 
355. 
356. 
357. 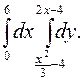
358. 
359. 
360. 
В задачах 361–380 вычислить объем тела, ограниченного указанными поверхностями. Данное тело и область интегрирования изобразить на чертеже.
361. 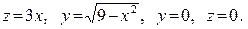
362. 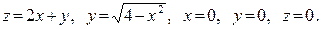
363. 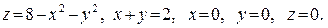
364. 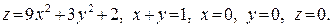
365. 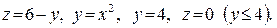
366. 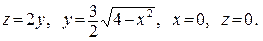
367. 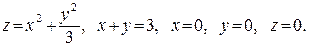
368. 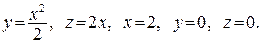
369. 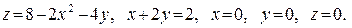
370. 
371. 
372. 
373. 
374. 
375. 
376. 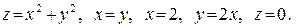
377. 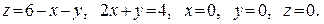
378. 
379. 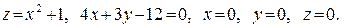
380.
В задачах 381-390 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.
381. .
.
382.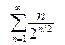 .
.
383. .
.
384. .
.
385.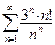 .
.
386. .
.
387.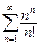 .
.
388. .
.
389.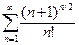 .
.
390.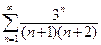 .
.
В задачах 391-400 исследовать сходимость рядов, пользуясь интегральным признаком сходимости Коши.
391. .
.
392. .
.
393. .
.
394.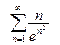 .
.
395. .
.
396.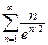 .
.
397. .
.
398.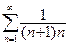 .
.
399. .
.
400.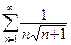 .
.
В задачах 401-420 дан степенной ряд  . Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения a, b и k даны.
. Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения a, b и k даны.
401.a = 2, b = 3, k = 4.
402.a = 6, b = 5, k = 3.
403.a = 3, b = 4, k = 5.
404.a = 5, b = 2, k = 4.
405.a = 4, b = 3, k = 3.
406.a = 2, b = 3, k = 5.
407.a = 5, b = 6, k = 2.
408.a = 3, b = 5, k = 6.
409.a = 3, b = 7, k = 3.
410.a = 2, b = 7, k = 3.
411.a = 5, b = 3, k = 4.
412.a = 4, b = 2, k = 2.
413.a = 7, b = 4, k = 5.
414.a = 2, b = 6, k = 3.
415.a = 4, b = 2, k = 4.
416.a = 6, b = 3, k = 5.
417.a = 5, b = 8, k = 6.
418.a = 4, b = 3, k = 2.
419.a = 2, b = 4, k = 7.
420.a = 3, b = 5, k = 3.
В задачах 421-440 требуется вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
421. .
.
422. .
.
423.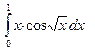 .
.
424. .
.
425.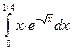 .
.
426. .
.
427. .
.
428.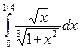 .
.
429. .
.
430.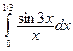 .
.
431. .
.
432.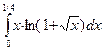 .
.
433.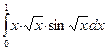 .
.
434. .
.
435. .
.
436.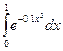 .
.
437. .
.
438.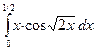 .
.
439. .
.
440.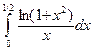 .
.
В задачах 441-460 при указанных начальных условиях найти три первых (отличных от нуля) члена разложения в степенной ряд Маклорена функции у(х), являющейся частным решением дифференциального уравнения:
441. .
.
442.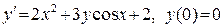 .
.
443. .
.
444. .
.
445.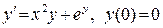 .
.
446. .
.
447.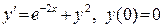 .
.
448. .
.
449.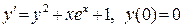 .
.
450. .
.
451.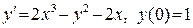 .
.
452.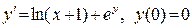 .
.
453.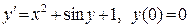 .
.
454.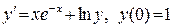 .
.
455. .
.
456.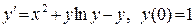 .
.
457. .
.
458. .
.
459. .
.
460. .
.
В задачах 461–470 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
461. .
462. .
463. .
464. 
465. .
466. .
467. .
468. .
469. .
470. .
В задачах 471–480найти частное решение дифференциального уравнения, удовлетворяющее указанным начальным условиям.
471. , .
472. , .
473. , .
474. , .
475. , .
476. , .
477. , .
478. , .
479. , .
480. , .
В задачах 481–500даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
481. , , .
482. , , .
483. , , .
484. , , .
485. , , .
486. , , .
487. , , .
488. , , .
489. , , .
490. , , .
491. , , .
492. , , .
493. , , .
494. , , .
495. , , .
496. , , .
497. , , .
498. , , .
499. , , .
500. , , .
В задачах 501 – 520даны линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.
501. , , .
502. , , .
503. , , .
504. , , .
505. , , .
506. , , .
507. , , .
508. , , .
509. , , .
510. , , .
511. , , .
512. , , .
513. , , .
514. , , .
515. , , .
516. , , .
517. , , .
518. , , .
519. , , .
520. , ,.
В задачах 521-530требуется решить систему уравнений и выделить частные решения, удовлетворяющие указанным начальным условиям.
521.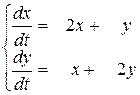 ,
, 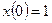 ,
,  .
.
522., , .
523., , .
524., , .
525., , .
526., , .
527., , .
528., , .
529., , .
530. ,, .
531.Найти уравнение кривой, проходящей через точку А(2;3) и обладающей тем свойством, что отрезок любой касательной к кривой, заключенный между осями координат, делится в точке касания пополам. Построить кривую.
532.Найти уравнение кривой, проходящей через точку А(2;4), если угловой коэффициент касательной в любой точке кривой в три раза больше углового коэффициента прямой, соединяющей ту же точку с началом координат. Построить кривую.
533.Найти уравнение кривой, проходящей через точку А (1;1) и обладающей тем свойством, что отрезок касательной на оси ординат, равен квадрату абсциссы точки касания. Построить кривую.
534.Найти уравнение кривой, проходящей через точку А (1;2) и обладающей тем свойством, что отрезок касательной между точкой касания и осью Ox делится пополам в точке пересечения с осью Oy. Построить кривую.
535.Найти уравнение кривой, проходящей через точку А(-1;1), если угловой коэффициент касательной в любой точке кривой равен квадрату ординаты точки касания. Построить кривую.
536.Найти уравнение кривой, проходящей через точку А(1;2), если поднормаль в каждой точке равна 2. Построить кривую.
537.Найти уравнение кривой, проходящей через точку А(2;4), если угловой коэффициент касательной в любой точке кривой в два раза меньше углового коэффициента прямой, соединяющей ту же точку с началом координат. Построить кривую.
538.Найти уравнение кривой, проходящей через точку А(2;-4), если начальная ордината касательной, проведенной в любой точке кривой, равна кубу абсциссы точки касания. Построить кривую.
539.Найти уравнение кривой, проходящей через точку А(0;3), если угловой коэффициент касательной в любой её точке, меньше ординаты точки касания на 2. Построить кривую.
540.Найти уравнение кривой, проходящей через точку А(2;2), если длина отрезка касательной между точкой касания и осью Ox равна длине отрезка между точкой касания и началом координат. Построить кривую.
В задачах 541-545 использовать формулу Бернулли для определения вероятностей появления события при повторении испытаний.
541.Всхожесть семян некоторого сорта пшеницы составляет 85%. Найти вероятность того, что из пяти посеянных семян взойдут: а) три; б) не менее трех.
542.В хлопке число длинных волокон составляет 80%. Какова вероятность того, что среди взятых наудачу 6 волокон длинных окажется: а) четыре; б) не более двух.
543.Принимая вероятность рождения мальчика равной 0,51, найти вероятность того, что среди 5 новорожденных: а) 4 мальчика; б) не более двух девочек.
544.В некотором водоеме караси составляют 80%.Найти вероятность того, что из 5 выловленных в этом водоеме рыб окажется: а) 3 карася; б) не менее 4 карасей.
545.Прибор состоит из 3 узлов. Вероятность безотказной работы в течение смены для каждого узла равна 0,8. Узлы выходят из строя независимо один от другого. Найти вероятность того, что за смену откажут: а) два узла; б) не менее двух узлов; в) все узлы.
В задачах 546—550 использовать асимптотическую формулу Пуассона для определения вероятностей появления события при повторении испытаний.
546.Семена содержат 0,15% сорняков. Какова вероятность при случайном отборе 2000 семян обнаружить 6 семян сорняков?
547.Вероятность появления бракованной детали равна 0,006. Найти вероятность того, что из 500 случайно отобранных деталей окажется 5 бракованных.
548.Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение часа равна 0,002. Найти вероятность того, что за час откажут 4 элемента.
549.Книга издана тиражом в 100000 экземпляров. Вероятность того, что в книге имеется дефект брошюровки равна 0,0001. Найти вероятность того, что тираж содержит 5 неправильно сброшюрованных книг.
550.Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останется не менее 2 бактерий.
В задачах 551-560 дано, что на шинном заводе рабочий за смену изготовляет п деталей. Вероятность того, что деталь окажется первого сорта равна р. Какова вероятность, что деталей первого сорта будет т штук.
551.п = 500, р=0,8, m = 380.
552.п = 400, р = 0,9, т = 362.
553.п = 400, р = 0,75, т = 320.
554.п = 600, р = 0,6, m = 355.
555.п = 635, р = 0,65, m = 400.
556.n =195, p=0,75, m =160.
557.n = 245, р = 0,8, m =185.
558.п = 100, р = 0, m = 94
559.п= 250, р = 0,6, m =155.
560.n = 725, р = 0,8, m = 560.
В задачах 561–580 дана вероятность р появления события A в каждом из n независимых испытаний. Пользуясь интегральной теоремой Лапласа, найти вероятность того, что в этих испытаниях событие А появится не менее m1 раз и не более m2 раза.
561.n= 150, р = 0,6, m1 = 78, m2 = 96.
562.n= 100, р=0,8, m1 = 72, m2 = 84.
563.n = 400, p = 0,9, m1 = 345, m2=372.
564.n = 600, p = 0,4, m1 = 210, m2 = 252.
565.n = 300, p = 0,75, m1 = 210, m2 = 225.
566.n = 625, p = 0,36, m1 = 225, m2 = 255.
567.n = 400, p = 0,5, m1= 190, m2 = 215.
568.n = 225, p = 0,2, m1 = 45, m2 = 60.
569.n = 300, p = 0,25, m1 = 75, m2 = 90.
570.n = 625, p = 0,64, m1 = 400, m2 = 430.
571.n = 140, p = 0,6, m1 = 88, m2 = 96.
572.n = 120, p = 0,8, m1 = 82, m2 = 94.
573.n = 410, p = 0,9, m1 = 360, m2 = 390.
574.n = 600, p = 0,4, m1 = 220, m2 =242.
575.n = 310, p = 0,75, m1 = 210, m2 = 235.
576.n = 625, p = 0,36, m1 = 240, m2 = 280.
577.n = 400, p = 0,5, m1 = 220, m2 = 250.
578.n = 225, p = 0,2, m1 = 50, m2 = 80.
579.n = 300, p = 0,25, m1 = 85, m2 = 90.
580.n = 625, p = 0,64, m1 = 410, m2 = 430.
В задачах 581–600 задан закон распределения случайной величины X (в первой строке таблицы даны возможные значения величины X, а во второй строке указаны вероятности р этих возможных значений).
Найти: 1) математическое ожидание М(Х); 2) дисперсию D(Х); 3) среднее квадратическое отклонение σ.
| 581. | Х | ||||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
| 582. | Х | ||||
| Р | 0,1 | 0,2 | 0,3 | 0,4 |
| 583. | Х | ||||
| Р | 0,2 | 0,2 | 0,1 | 0,5 |
| 584. | Х | ||||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
| 585. | Х | ||||
| Р | 0,2 | 0,2 | 0,15 | 0,45 |
| 586. | Х | ||||
| Р | 0,1 | 0,3 | 0,4 | 0,2 |
| 587. | Х | ||||
| Р | 0,2 | 0,3 | 0,2 | 0,3 |
| 588. | Х | ||||
| Р | 0,1 | 0,2 | 0,3 | 0,4 |
| 589. | Х | ||||
| Р | 0,2 | 0,15 | 0,25 | 0,4 |
| 590. | Х | ||||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
| 591. | Х | ||||
| Р | 0,1 | 0,4 | 0,1 | 0,4 |
| 592. | Х | ||||
| Р | 0,2 | 0,2 | 0,3 | 0,3 |
| 593. | Х | ||||
| Р | 0,2 | 0,2 | 0,2 | 0,4 |
| 594. | Х | ||||
| Р | 0,1 | 0,4 | 0,1 | 0,4 |
| 595. | Х | ||||
| Р | 0,2 | 0,1 | 0,1 | 0,6 |
| 596. | Х | ||||
| Р | 0,2 | 0,3 | 0,1 | 0,4 |
| 597. | Х | ||||
| Р | 0,2 | 0,2 | 0,2 | 0,4 |
| 598. | Х | ||||
| Р | 0,1 | 0,3 | 0,2 | 0,4 |
| 599. | Х | ||||
| Р | 0,1 | 0,4 | 0,1 | 0,4 |
| 600. | Х | ||||
| Р | 0,2 | 0,2 | 0,1 | 0,5 |
В задачах 601–620дано, что втулки, выпускаемые цехом, по размеру внешнего диаметра распределены по нормальному закону. Стандартная длина внешнего диаметра втулки (математическое ожидание) равна  мм, среднее квадратическое отклонение –
мм, среднее квадратическое отклонение –  мм. Найти: 1) вероятность того, что внешний диаметр наудачу взятой втулки будет больше
мм. Найти: 1) вероятность того, что внешний диаметр наудачу взятой втулки будет больше  мм и меньше
мм и меньше  мм; 2) вероятность того, что внешний диаметр втулки отклонится от стандартной длины не более чем на
мм; 2) вероятность того, что внешний диаметр втулки отклонится от стандартной длины не более чем на  мм. Значения
мм. Значения  ,
,  ,
,  ,
,  ,
,  даны.
даны.
| 601. |  =120 =120
|  =5 =5
|  =112 =112
|  =124 =124
|  =3 =3
|
| 602. |  =124 =124
|  =5 =5
|  =120 =120
|  =127 =127
|  =2 =2
|
| 603. |  =114 =114
|  =3 =3
|  =112 =112
|  =116 =116
|  =1,5 =1,5
|
| 604. |  =110 =110
|  =4 =4
|  =108 =108
|  =114 =114
|  =2 =2
|
| 605. |  =50 =50
|  =5 =5
|  =42 =42
|  =54 =54
|  =2 =2
|
| 606. |  =80 =80
|  =4 =4
|  =76 =76
|  =84 =84
|  =1 =1
|
| 607. |  =100 =100
|  =2 =2
|  =106 =106
|  =112 =112
|  =2 =2
|
| 608. |  =90 =90
|  =5 =5
|  =87 =87
|  =94 =94
|  =1,5 =1,5
|
| 609. |  =75 =75
|  =4 =4
|  =72 =72
|  =78 =78
|  =2,5 =2,5
|
| 610. |  =95 =95
|  =3 =3
|  =90 =90
|  =99 =99
|  =2 =2
|
| 611. |  =85 =85
|  =3 =3
|  =83 =83
|  =88 =88
|  =3 =3
|
| 612. |  =90 =90
|  =5 =5
|  =86 =86
|  =92 =92
|  =1 =1
|
| 613. |  =85 =85
|  =5 =5
|  =84 =84
|  =89 =89
|  =2 =2
|
| 614. |  =86 =86
|  =4 =4
|  =84 =84
|  =90 =90
|  =3 =3
|
| 615. |  =112 =112
|  =2 =2
|  =110 =110
|  =114 =114
|  =1,5 =1,5
|
| 616. |  =100 =100
|  =3 =3
|  =106 =106
|  =111 =111
|  =1 =1
|
| 617. |  =116 =116
|  =4 =4
|  =115 =115
|  =117 =117
|  =3 =3
|
| 618. |  =114 =114
|  =5 =5
|  =112 =112
|  =118 =118
|  =2 =2
|
| 619. |  =120 =120
|  =2 =2
|  =116 =116
|  =124 =124
|  =3,5 =3,5
|
| 620. |  =115 =115
|  =4 =4
|  =112 =112
|  =118 =118
|  =2,5 =2,5
|
ПРИЛОЖЕНИЕ
Таблица 1
Значение функции 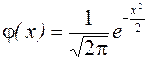 .
.
| х | ||||||||||
| 0,0 | 0,3989 | 0,3989 | 0,3989 | 0,3988 | 0,3986 | 0,3984 | 0,3982 | 0,3980 | 0,3977 | 0,3973 |
| 0,1 | 0,3970 | 0,3965 | 0,3961 | 0,3956 | 0,3951 | 0,3945 | 0,3939 | 0,3932 | 0,3925 | 0,3918 |
| 0,2 | 0,3910 | 0,3902 | 0,3894 | 0,3885 | 0,3876 | 0,3867 | 0,3857 | 0,3847 | 0,3836 | 0,3825 |
| 0,3 | 0,3814 | 0,3802 | 0,3790 | 0,3778 | 0,3765 | 0,3752 | 0,3739 | 0,3726 | 0,3712 | 0,3697 |
| 0,4 | 0,3683 | 0,3668 | 0,3653 | 0,3637 | 0,3621 | 0,3605 | 0,3589 | 0,3572 | 0,3555 | 0,3538 |
| 0,5 | 0,3521 | 0,3503 | 0,3485 | 0,3467 | 0,3448 | 0,3429 | 0,341 | 0,3391 | 0,3372 | 0,3352 |
| 0,6 | 0,3332 | 0,3312 | 0,3292 | 0,3271 | 0,3251 | 0,3230 | 0,3209 | 0,3187 | 0,3166 | 0,3144 |
| 0,7 | 0,3123 | 0,3101 | 0,3079 | 0,3056 | 0,3034 | 0,3011 | 0,2989 | 0,2966 | 0,2943 | 0,2920 |
| 0,8 | 0,2897 | 0,2874 | 0,2850 | 0,2827 | 0,2803 | 0,2780 | 0,2756 | 0,2732 | 0,2709 | 0,2685 |
| 0,9 | 0,2661 | 0,2637 | 0,2613 | 0,2589 | 0,2565 | 0,2541 | 0,2516 | 0,2492 | 0,2468 | 0,2444 |
| 1,0 | 0,2420 | 0,2396 | 0,2371 | 0,2347 | 0,2323 | 0,2299 | 0,2275 | 0,2251 | 0,2227 | 0,2203 |
| 1,1 | 0,2179 | 0,2155 | 0,2131 | 0,2107 | 0,2083 | 0,2059 | 0,2036 | 0,2012 | 0,1989 | 0,1965 |
| 1,2 | 0,1942 | 0,1919 | 0,1895 | 0,1872 | 0,1849 | 0,1826 | 0,1804 | 0,1781 | 0,1758 | 0,1736 |
| 1,3 | 0,1714 | 0,1691 | 0,1669 | 0,1647 | 0,1626 | 0,1604 | 0,1582 | 0,1561 | 0,1539 | 0,1518 |
| 1,4 | 0,1497 | 0,1476 | 0,1456 | 0,1435 | 0,1415 | 0,1394 | 0,1374 | 0,1354 | 0,1334 | 0,1315 |
| 1,5 | 0,1295 | 0,1276 | 0,1257 | 0,1238 | 0,1219 | 0,1200 | 0,1182 | 0,1163 | 0,1145 | 0,1127 |
| 1,6 | 0,1109 | 0,1092 | 0,1074 | 0,1057 | 0,1040 | 0,1023 | 0,1006 | 0,0989 | 0,0973 | 0,0957 |
| 1,7 | 0,0940 | 0,0925 | 0,0909 | 0,0893 | 0,0878 | 0,0863 | 0,0848 | 0,0833 | 0,0818 | 0,0804 |
| 1,8 | 0,0790 | 0,0775 | 0,0761 | 0,0748 | 0,0734 | 0,0721 | 0,0707 | 0,0694 | 0,0681 | 0,0669 |
| 1,9 | 0,0656 | 0,0644 | 0,0632 | 0,0620 | 0,0608 | 0,0596 | 0,0584 | 0,0573 | 0,0562 | 0,0551 |
| 2,0 | 0,0540 | 0,0529 | 0,0519 | 0,0508 | 0,0498 | 0,0488 | 0,0478 | 0,0468 | 0,0459 | 0,0449 |
| 2,1 | 0,0440 | 0,0431 | 0,0422 | 0,0413 | 0,0404 | 0,0396 | 0,0387 | 0,0379 | 0,0371 | 0,0363 |
| 2,2 | 0,0355 | 0,0347 | 0,0339 | 0,0332 | 0,0325 | 0,0317 | 0,031 | 0,0303 | 0,0297 | 0,0290 |
| 2,3 | 0,0283 | 0,0277 | 0,0270 | 0,0264 | 0,0258 | 0,0252 | 0,0246 | 0,0241 | 0,0235 | 0,0229 |
| 2,4 | 0,0224 | 0,0219 | 0,0213 | 0,0208 | 0,0203 | 0,0198 | 0,0194 | 0,0189 | 0,0184 | 0,0180 |
| 2,5 | 0,0175 | 0,0171 | 0,0167 | 0,0163 | 0,0158 | 0,0154 | 0,0151 | 0,0147 | 0,0143 | 0,0139 |
| 2,6 | 0,0136 | 0,0132 | 0,0129 | 0,0126 | 0,0122 | 0,0119 | 0,0116 | 0,0113 | 0,0110 | 0,0107 |
| 2,7 | 0,0104 | 0,0101 | 0,0099 | 0,0096 | 0,0093 | 0,0091 | 0,0088 | 0,0086 | 0,0084 | 0,0081 |
| 2,8 | 0,0079 | 0,0077 | 0,0075 | 0,0073 | 0,0071 | 0,0069 | 0,0067 | 0,0065 | 0,0063 | 0,0061 |
| 2,9 | 0,0060 | 0,0058 | 0,0056 | 0,0055 | 0,0053 | 0,0051 | 0,005 | 0,0048 | 0,0047 | 0,0046 |
| 3,0 | 0,0044 | 0,0043 | 0,0042 | 0,0040 | 0,0039 | 0,0038 | 0,0037 | 0,0036 | 0,0035 | 0,0034 |
| 3,1 | 0,0033 | 0,0032 | 0,0031 | 0,0030 | 0,0029 | 0,0028 | 0,0027 | 0,0026 | 0,0025 | 0,0025 |
| 3,2 | 0,0024 | 0,0023 | 0,0022 | 0,0022 | 0,0021 | 0,0020 | 0,0020 | 0,0019 | 0,0018 | 0,0018 |
| 3,3 | 0,0017 | 0,0017 | 0,0016 | 0,0016 | 0,0015 | 0,0015 | 0,0014 | 0,0014 | 0,0013 | 0,0013 |
| 3,4 | 0,0012 | 0,0012 | 0,0012 | 0,0011 | 0,0011 | 0,0010 | 0,0010 | 0,0010 | 0,0009 | 0,0009 |
| 3,5 | 0,0009 | 0,0008 | 0,0008 | 0,0008 | 0,0008 | 0,0007 | 0,0007 | 0,0007 | 0,0007 | 0,0006 |
| 3,6 | 0,0006 | 0,0006 | 0,0006 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0005 | 0,0004 |
| 3,7 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0004 | 0,0003 | 0,0003 | 0,0003 | 0,0003 |
| 3,8 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0003 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 |
| 3,9 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0002 | 0,0001 | 0,0001 |
Таблица 2
Значение функции 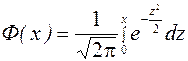 .
.
| x | 
| x | 
| x | 
| x | 
| x | 
|
| 0,00 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09 0,10 0,11 0,12 0,13 0,14 0,15 0,16 0,17 0,18 0,19 0,20 0,21 0,22 0,23 0,24 0,25 | 0,00 00 0,00 40 0,00 80 0,01 20 0,01 60 0,01 99 0,02 39 0,02 79 0,03 19 0,03 59 0,03 98 0,04 38 0,04 78 0,05 17 0,05 57 0,05 96 0,0636 0,06 75 0,07 14 0,07 53 0,07 93 0,08 32 0,08 71 0,09 10 0,09 48 0,09 87 | 0,26 0,27 0,28 0,29 0,30 0,31 0,32 0,33 0,34 0,35 0,36 0,37 0,39 0,40 0,41 0,42 0,43 0,44 0,45 0,46 0,47 0,48 0,49 0,50 0,51 | 0,10 26 0,10 64 0,11 03 0,11 41 0,11 79 0,12 17 0,12 55 0,12 93 0,13 31 0,13 68 0,14 06 0,14 43 0,14 80 0,15 17 0,15 54 0,15 91 0,16 28 0,16 64 0,17 00 0,17 36 0,17 72 0,18 08 0,18 44 0,18 79 0,19 15 0,19 50 | 0,52 0,53 0,54 0,55 0,56 0,57 0,58 0,59 0,60 0,61 0,62 0,63 0,64 0,65 0,66 0,67 0,68 0,69 0,70 0,71 0,72 0,73 0,74 0,75 0,76 0,77 | 0,19 85 0,20 19 0,20 54 0,20 88 0,21 23 0,21 57 0,21 90 0,22 24 0,22 57 0,22 91 0,23 24 0,23 57 0,23 89 0,24 22 0,24 54 0,24 86 0,25 17 0,25 49 0,25 80 0,26 11 0,26 42 0,26 73 0,27 03 0,27 34 0,27 64 0,27 94 | 0,78 0,79 0,80 0,81 0,82 0,83 0,84 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 0,98 0,99 1,00 1,01 1,02 1,03 | 0,28 23 0,28 52 0,28 81 0,29 10 0,29 39 0,29 67 0,29 95 0,30 23 0,30 51 0,30 78 0,31 06 0,31 33 0,31 59 0,31 86 0,32 12 0,32 38 0,32 64 0,32 89 0,33 15 0,33 40 0,33 65 0,33 89 0,34 13 0,34 38 0,34 61 0,34 85 | 1,04 1,05 1,06 1,07 1,08 1,09 1,10 1,11 1,12 1,13 1,14 1,15 1,16 1,17 1,18 1,19 1,20 1,21 1,22 1,23 1,24 1,25 1,26 1,27 1,28 1,29 | 0,35 08 0,35 31 0,35 54 0,35 77 0,35 99 0,36 21 0,36 43 0,36 65 0,36 86 0,37 08 0,37 29 0,37 49 0,37 70 0,37 90 0,38 10 0,38 30 0,38 49 0,38 69 0,38 83 0,39 07 0,39 25 0,39 44 0,39 62 0,39 80 0,39 97 0,40 15 |
Продолжение таблицы 2
| X | 
| x | 
| x | 
| x | 
| x | 
|
| 1,30 1,31 1,32 1,33 1,34 1,35 1,36 1,37 1,38 1,39 1,40 1,41 1,42 1,43 1,44 1,45 1,46 1,47 1,48 1,49 1,50 1,51 1,52 1,53 1,54 1,55 | 0,40 32 0,40 49 0,40 66 0,40 82 0,40 99 0,41 15 0,41 31 0,41 47 0,41 62 0,41 77 0,41 92 0,42 07 0,42 22 0,42 36 0,42 51 0,42 65 0,42 79 0,42 92 0,43 06 0,43 19 0,43 32 0,43 45 0,43 57 0,43 70 0,43 82 0,43 94 | 1,56 1,57 1,58 1,59 1,60 1,61 1,62 1,63 1,64 1,65 1,66 1,67 1,68 1,69 1,70 1,71 1,72 1,73 1,74 1,75 1,76 1,77 1,78 1,79 1,80 1,81 | 0,44 06 0,44 18 0,44 29 0,44 41 0,44 52 0,44 63 0,44 74 0,44 84 0,44 95 0,45 05 0,45 15 0,45 25 0,45 35 0,45 45 0,45 54 0,45 64 0,45 73 0,45 82 0,45 91 0,45 99 0,46 08 0,46 16 0,46 25 0,46 33 0,46 41 0,46 49 | 1,82 1,83 1,84 1,85 1,86 1,87 1,88 1,89 1,90 1,91 1,92 1,93 1,94 1,95 1,96 1,97 1,98 1,99 2,00 2,02 2,04 2,06 2,08 2,10 2,12 2,14 | 0,46 56 0,46 64 0,46 71 0,46 78 0,46 86 0,46 93 0,46 99 0,47 06 0,47 13 0,47 19 0,47 26 0,47 32 0,47 38 0,47 44 0,47 50 0,47 56 0,47 61 0,47 67 0,47 72 0,47 83 0,47 93 0,48 03 0,48 12 0,48 21 0,48 30 0,48 38 | 2,16 2,18 2,20 2,22 2,24 2,26 2,28 2,30 2,32 2,34 2,36 2,38 2,40 2,42 2,44 2,46 2,48 2,50 2,52 2,54 2,56 2,58 2,60 2,62 2,64 2,66 | 0,48 46 0,48 54 0,48 61 0,48 68 0,48 75 0,48 81 0,48 87 0,48 93 0,48 98 0,49 04 0,49 09 0,49 13 0,49 18 0,49 22 0,49 27 0,49 31 0,49 34 0,49 38 0,49 41 0,49 45 0,49 48 0,49 51 0,49 53 0,49 56 0,49 59 0,49 61 | 2,68 2,70 2,72 2,74 2,76 2,78 2,80 2,82 2,84 2,86 2,88 2,90 2,92 2,94 2,96 2,98 3,00 3,20 3,40 3,60 3,80 4,00 4,50 5,00 | 0,49 63 0,49 65 0,49 67 0,49 69 0,49 71 0,49 73 0,49 74 0,49 76 0,49 77 0,49 79 0,49 80 0,49 81 0,49 82 0,49 84 0,49 85 0,49 86 0,49 865 0,49 931 0,49 966 0,49 984 1 0,49 992 8 0,49 996 8 0,49 999 7 0,49 999 7 |
ЛИТЕРАТУРА
1. Ефимов Н.В. Краткий курс аналитической геометрии. – М.: Наука, 1975.
2. Пискунов Н.С. Дифференциальное и интегральное исчисления. – М.: Наука, 1970-1978, т. 1, 2.
3. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа (любое издание).
4. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1962. – 404с.
5. Минорский В.П. Сборник задач по высшей математике. – М.: Наука, 1955-1977.
6. Лихолетов И.И., Мацкевич И.П. Руководство к решению задач по высшей математике, теории вероятностей и математической статистике. – Минск: Вышейшая школа, 1976. – 456с.
7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа (любое издание).
8. Высшая математика: Методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей сельскохозяйственных высших учебных заведений / Штейнгардт Д.А. – 5-е изд. – М.: Высшая школа, 1990. – 127с.
9. Высшая математика: методические указания и контрольные задания для студентов-заочников инженерно-технических специальностей сельскохозяйственных высших учебных заведений / Н.А. Абакумова, О.Г. Бельчикова, Н.Л. Гамершмид, В.М. Щербаков. - Барнаул: Изд-во АГАУ, 2006. - 108с.
Содержание
ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ.. 4
ТАБЛИЦЫ ВАРИАНТОВ.. 5
УКАЗАНИЯ К ВЫПОЛНЕНИЮ КОНТРОЛЬНЫХ РАБОТ.. 5
Тема 1. Элементы аналитической геометрии на плоскости. 5
Тема 2. Основы векторной алгебры.. 5
Тема 3. Элементы аналитической геометрии в пространстве. 5
Тема 4. Элементы линейной алгебры.. 5
Тема 5. Введение в анализ. 5
Тема 6 Производная и дифференциал. 5
Тема 7. Исследование поведения функции. 5
Тема 8. Неопределенный интеграл. 5
Тема 9. Определенный интеграл. 5
Тема 10. Приложения определенного интеграла. 5
Тема 11. Функции нескольких переменных. 5
Тема 12. Кратные интегралы. Криволинейный интеграл. 5
Тема 13. Ряды и их приложения. 5
Тема 14. Дифференциальные уравнения первого порядка. 5
Тема 15. Дифференциальные уравнения второго порядка. 5
Тема 16. Основы теории вероятностей. 5
ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ.. 5
ПРИЛОЖЕНИЕ.. 5
ЛИТЕРАТУРА.. 5
– Конец работы –
Используемые теги: методические, указания, Контрольные, задания, высшей, математике0.095
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: МЕТОДИЧЕСКИЕ УКАЗАНИЯ И КОНТРОЛЬНЫЕ ЗАДАНИЯ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов