Тема 12. Кратные интегралы. Криволинейный интеграл.
Пискунов, гл. XIV, §1—3, упр. 1 – 6, 8—16; §4, упр. 24—29, 31 — 36; §5, упр. 18—20, 38—40; § 7, упр. 43—47; § 8—10, упр. 51—54, 57, 64; § 11—14, упр. 65—68. Гл. XV, § 1—2 упр. 1—5. Разберите решения задачи 28 из данного пособия.
Задача 28. Дан интеграл 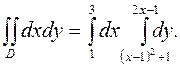
 Требуется:
Требуется:
1) построить на плоскости хОу область интегрирования D;
2) изменить порядок интегрирования;
3) вычислить площадь области D при заданном и измененном порядке интегрирования.
Решение:
1. Пределы внешнего интеграла по переменной х — числа 1 и 3 — указывают на то, что область D ограничена слева прямой х = 1 и справа прямой х = 3.
Пределы внутреннего интеграла по переменной у указывают на то, что область D ограничена снизу параболой 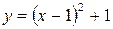 и сверху прямой
и сверху прямой  Построив эти линии на отрезке [1; 3], получим область D (рис. 12).
Построив эти линии на отрезке [1; 3], получим область D (рис. 12).
2. Чтобы изменить порядок интегрирования, установим пределы интегрирования для внешнего интеграла по переменной у. Как видно из рис. 12 наименьшее значение, которое принимает у в области D, равно 1 в точке А(1; 1), а наибольшее значение равно 5 в точке В(3; 5). Следовательно, внешний интеграл по переменной у будет иметь пределы: 1 (нижний предел) и 5 (верхний предел).
Определим пределы для внутреннего интеграла по переменной х.
Из уравнения прямой 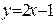 получаем
получаем 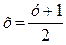 нижний предел.
нижний предел.
Из уравнения параболы 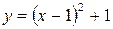 получаем
получаем  – верхний предел. Таким образом,
– верхний предел. Таким образом,

3. Вычислим площадь области D при заданном порядке интегрирования:

4. Вычислим площадь области D при измененном порядке интегрирования: