ЗАДАЧИ ДЛЯ КОНТРОЛЬНЫХ РАБОТ

 

В задачах 1—20 даны координаты вершин треугольника ABC. Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и ВС и их угловые коэффициенты; 3) угол В в радианах с точностью до двух знаков; 4) уравнение высоты CD и ее длину; 5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой CD; 6) уравнение прямой, проходящей через точку К, параллельно стороне АВ; 7) координаты точки М, расположенной симметрично точке А относительно прямой CD.

1.A(-7;-2), B(5;-11), C(9;11).

2.A(-4;8), B(8;-1), C(12;21).

3.A(-11;0), B(1;-9), C(5;13).

4.A(-9;10), B(3;1), C(7;23).

5.A(1;3), B(13;-6), C(17;16).

6.A(-8;7), B(4;-2), C(8;20).

7.A(2;1), B(14;-8), C(18;14).

8.A(-3;11), B(9;2), C(13;24).

9.A(3;6), B(15;-3), C(19;19).

10.A(0;5), B(12;-4), C(16;18).

11.A(-1;8), B(11;-1), C(9;13).

12.A(-5;9), B(7;0), C(5;14).

13.A(4;7), B(16;-2), C(14;12).

14.A(-9;6), B(3;-3), C(1;11).

15.A(-3;12), B(9;3), C(7;17).

16.A(-2;11), B(10;2), C(8;16).

17.A(5;2), B(17;-7), C(15;7).

18.A(-6;5), B(6;-4), C(4;10).

19.A(1;4), B(13;-5), C(11;9).

20.A(-4;10), B(8;1), C(6;15).

В задачах 21—25 составить уравнение геометрического места точек, равноудаленных от данной точки А (x₁, у₁) и данной прямой y=b. Полученное уравнение привести к простейшему виду и затем построить кривую.

21.A(2,5), y=1.

22.A(3,-4), y=2.

23.A(-4,3), y=-1.

24.A(-2,-3), y=-1.

25.A(1,-1), y=3.

В задачах 26—30 составить уравнение геометрического места точек, отношение расстояний которых до данной точки А (х₁; у₁) и до данной прямой x=а равночислу . Полученное уравнение привести к простейшему виду и затем построить кривую.

26.A(6,0), x=1,5, =2.

27.A(3,0), x=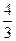, =1,5.

28.A(10,0), x=2,5, 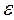=2.

29.A(2,0), x=4,5, =2/3.

30.A(3,0), x=12, =0,5.

В задачах 31—35даны координаты точек А(х₁;у₁), b(х₂, у₂) и радиус окружности R, центр которой находится в начале координат. Требуется: 1) составить каноническое уравнение эллипса, проходящего через данные точки А и В; 2) найти полуоси, фокусы и эксцентриситет этого эллипса; 3) найти все точки пересечения эллипса с данной окружностью; 4) построить эллипс и окружность.

31.A(4;-2), B(2;), R=.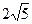

32.A(-8;4), B(;-2),R=.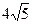

33.A(;-2), B(-3;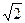), R=3.

34.A(-6;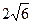),B(;6), R=8.

35.A(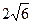;-4), B(6;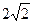), R=.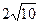

В задачах 36—40 даны координаты точек А (х₁;у₁) и В (х₂;y₂). Требуется: 1) составить каноническое уравнение гиперболы, проходящей через данные точки А и В, если фокусы гиперболы расположены на оси абсцисс; 2) найти полуоси, фокусы, эксцентриситет и уравнения асимптот этой гиперболы; 3) найти все точки пересечения гиперболы с окружностью с центром в начале координат, если эта окружность проходит через фокусы гиперболы; 4) построить гиперболу, ее асимптоты и окружность.

36.A(-3;4), B(-5;).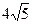

37.A(4;-6), B(6;).

38.A(-4;-3), B(8;9).

39.A(8;12), B(-6;).

40.A(8;6), B(10;-).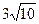

 

В задачах 41—60 решить систему трех уравнений с тремя неизвестными при помощи определителей (для студентов, обучающихся по сокращенной программе, систему решить любым способом).

41.

42.

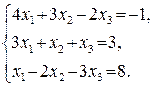
43.

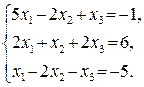
44.

45.

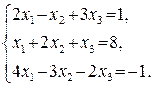
46.

47.

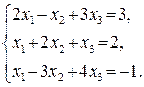
48.

49.

50.

51.

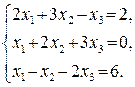
52.

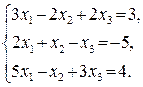
53.

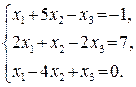
54.

55.

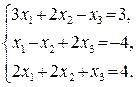
56.

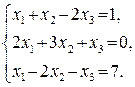
57.

58.

59.

60.

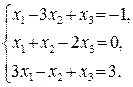
В задачах 61-80 дана невырожденная матрица А. Требуется: 1) найти обратную матрицу 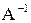; 2) пользуясь правилом умножения матриц, показать, что 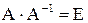, где 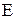— единичная матрица.

61.

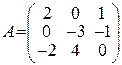
62.

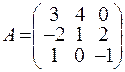
63.

64.

65.

66.

67.

68.

69.

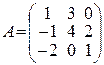
70.

71.

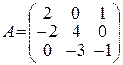
72.

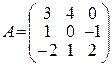
73.

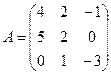
74.

75.

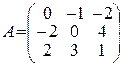
76.

77.

78.

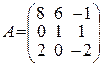
79.

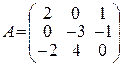
80.

В задачах 81-100 даны координаты вершин пирамиды АВСD. Требуется: 1) записать векторы 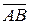, 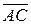и 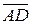в системе орт и найти модули этих векторов; 2) найти угол между векторам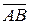и и 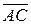; 3) найти проекцию вектора 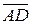на вектор 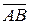; 4) найти площадь грани АВС; найти объем пирамиды АВСD.

81.A(2;-3;1), B(6;1;-1), C(4;8;-9), D(2; -1;2).

82.A(5;-1;-4), B(9;3;-6), C(7;10;-14), D(5; 1;-3).

83.A(1;-4;0), B(5;0;-2), C(3;7;-10), D(1;-2;1).

84.A(-3;-6;2), B(1;-2;0), C(-1;5;-8), D(-3;-4;3).

85.A(-1;1;-5), B(3;5;-7), C(1;12;-15), D(-1;3;-4).

86.A(-4;2;-1), B(0;6;-3), C(-2;13;-11), D(-4;4;0).

87.A(0;4;3), B(4;8;1), C(2;15;-7), D(0;6;4).

88.A(-2;0;-2), B(2;4;-4), C(0;11;-12), D(-2;2;-1).

89.A(3;3;-3), B(7;7;-5), C(5;14;-13), D(3;5;-2).

90.A(3;1;1), B(7;5;-1), C(5;12;-9), D(3;3;2).

91.A(0;1;3), B(1;-1;5), C(11;3;13), D(-2;1;7).

92.A(3;1;-2), B(4;-1;0), C(14;3;8), D(11;5;6).

93.A(-8;3;-1), B(-7;1;1),C(3;5;9), D(0;7;7).

94.A(2;-1;-4), B(3;-3;-2), C(13;1;6), D(10;3;4).

95.A(-4;5;-5), B(-3;3;-3), C(7;7;5), D(4;9;3).

96.A(-2;-3;2), B(-1;-5;4), C(9;-1;12), D(6;1;10).

97.A(-3;4;-3), B(-2;2;-1), C(8;6;7), D(5;8;5).

98.A(-5;2;-4), B(-4;0;-2), C(6;4;6), D(3;6;4).

99.A(-7;3;1), B(-6;1;3), C(4;5;11), D(1;7;9).

100.A(-6;-4;-3), B(-5;-6;-1), C(5;-2;7), D(2;0;5).

В задачах 101—110 данную систему уравнений записать в матричной форме и затем решить с помощью обратной матрицы.

101.

102.

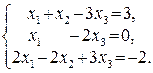
103.

104.

105.

106.

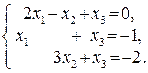
107.

108.

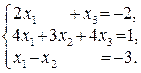
109.

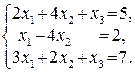
110.

В задачах 111—120данную систему уравнений решить методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы.

111.

112.

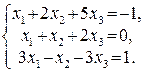
113.

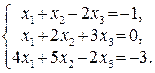
114.

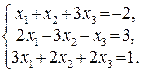
115.

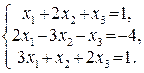
116.

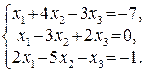
117.

118.

119.

120.

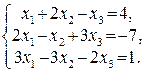
В задачах 121–140 вычислить указанные пределы: