Тема 8. Неопределенный интеграл
Пискунов, гл. X, § 1—3, упр. 1—7; § 4, упр. 8—50, 59—68, 70—79, 84—86, 94—100; § 5, упр. 102—111, 115, 118, 123, 125; § 6, упр. 127-137, 140, 142; § 7—9, упр. 152—160, 163, 164, 167; § 11, упр. 170—172, 174, 176, 178, 180; § 14, упр. 196—206, 208—214. Разберите решение задачи 21.
Задача 21.Найти неопределённые интегралы:
а) 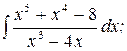 б)
б) ; в)
; в)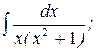 г)
г) 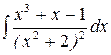 ; д)
; д) е)
е)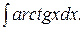 ; ж)
; ж)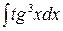 ; з)
; з)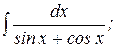 и)
и) 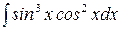 ; к)
; к)  ; л)
; л) 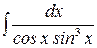 .
.
Решение: При нахождении неопределённых интегралов функций используют следующие свойства:
1) 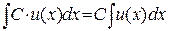 ,
,
2) 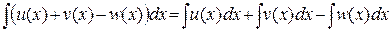
и таблицу интегралов основных элементарных функций:
1. 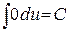 ;
;
2.  ;
;
3. 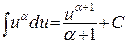 ;
;
4.  ;
;
5. 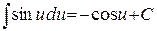 ;
;
6. 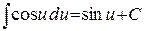 ;
;
7. 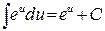 ;
;
8. 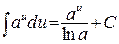 ;
;
9. 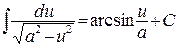 ;
;
9'. 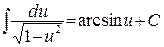
10. 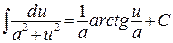 ;
;
10'. 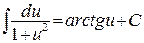 ;
;
11.  ;
;
11'.  ;
;
12.  ;
;
13.  ;
;
14. 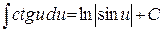 ;
;
15. 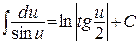 ;
;
16. 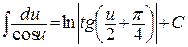 .
.
а) Подынтегральное выражение представляет собой неправильную рациональную дробь, так как степень многочлена, стоящего в числителе, больше степени многочлена, стоящего в знаменателе. Поэтому выделим целую часть дроби (разделим числитель на знаменатель с остатком).
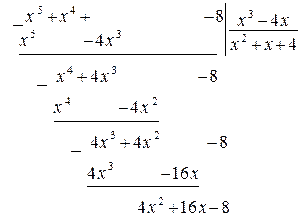
Тогда данную дробь можно записать в виде
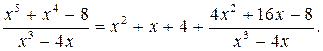
Правильная рациональная дробь может быть представлена в виде суммы простейших дробей четырёх типов: 1)  2)
2)  где m – целое число, большее единицы; 3)
где m – целое число, большее единицы; 3)  где
где 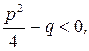 т. е. квадратный трёхчлен
т. е. квадратный трёхчлен  не имеет действительных корней; 4)
не имеет действительных корней; 4) 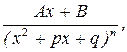 где n>1, n – целое число и квадратный трёхчлен
где n>1, n – целое число и квадратный трёхчлен  не имеет действительных корней.
не имеет действительных корней.
Выпишем знаменатель дроби и разложим его на множители

Знаменатель представляет собой произведение линейных множителей в первой степени, следовательно, дробь можно разложить на сумму простейших дробей первого типа.
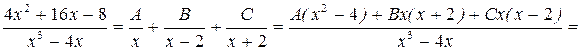

Приравниваем коэффициенты при одинаковых степенях многочленов, стоящих в числителях дробей

Решая систему, получим 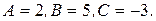
Значит, подынтегральная дробь представится в виде
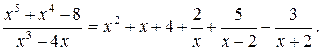
Следовательно,

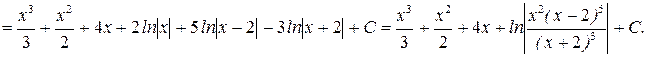
б) Подынтегральное выражение представляет собой правильную рациональную дробь. Разложим знаменатель на множители:
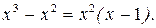
Выпишем подынтегральную дробь и разложим её на сумму простейших дробей первого и второго типа, т. к. знаменатель дроби представляет собой произведение линейных множителей, один из которых кратный.
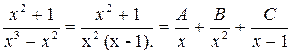 =
=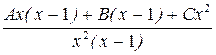 =
=
=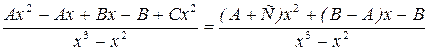 .
.
Приравняем коэффициенты многочленов, стоящих в числителе.
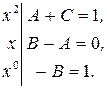
Решая данную систему, получим: 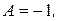

 Имеем:
Имеем:
 .
.
Таким образом, данный интеграл можно записать в виде:
 =
=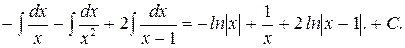
в) Подынтегральное выражение представляет собой правильную рациональную дробь. Выпишем подынтегральную дробь и разложим её на сумму простейших дробей первого и третьего типа, т. к. знаменатель представляет собой произведение линейного множителя в первой степени и квадратного трёхчлена  , не имеющего действительных корней, также в первой степени.
, не имеющего действительных корней, также в первой степени.
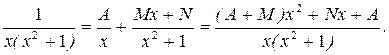

Решая данную систему, получим: 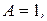

 Имеем
Имеем
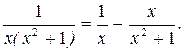
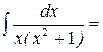


г) Подынтегральное выражение представляет собой правильную рациональную дробь. Выпишем подынтегральную дробь и разложим её на сумму простейших дробей третьего и четвёртого типа, т. к. знаменатель представляет собой квадратный трёхчлен  , не имеющего действительных корней, во второй степени.
, не имеющего действительных корней, во второй степени.
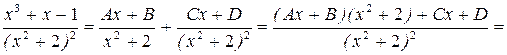
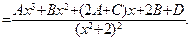

Решая данную систему, получим: 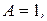
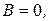

 Имеем
Имеем 
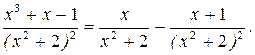 Тогда
Тогда


Отдельно найдём последний интеграл. Положим 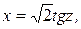 тогда
тогда 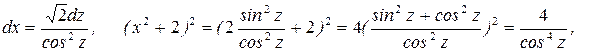
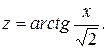 Получим
Получим
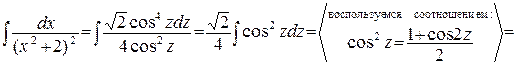
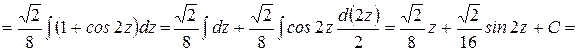

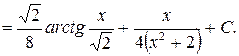
Окончательно получим

д) Сделаем замену 

 ,
,
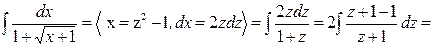
 =
=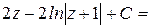
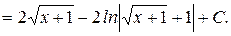
е) Интегрируем по частям по формуле: 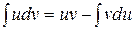 .
.

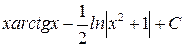 .
.
ж) Сделаем замену 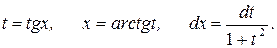 Получим
Получим
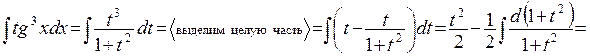

з) Сделаем замену
 Получим
Получим 
Последний интеграл есть интеграл от рациональной дроби. Выпишем эту дробь и разложим её на сумму простейших.
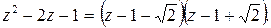

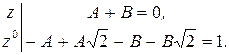
Решая систему, получим 
Тогда 
Следовательно, 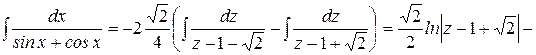
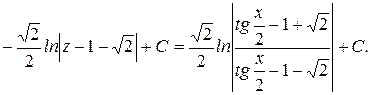
и) 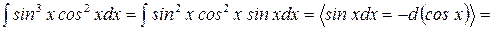

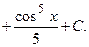
к) 
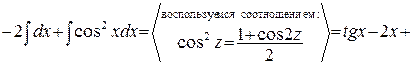
 л)
л)