Тема 9. Определенный интеграл
Пискунов, гл. XI, § 1—4, упр. 6—18; § 5, 6, упр. 19—25; § 7, упр. 29—41; § 8, упр. 44—47. Разберите решение задач 22, 23 из данного пособия.
Задача 22.Вычислить интеграл

Решение: Сделаем подстановку. Пусть 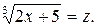
Тогда  Определим пределы интегрирования для переменной z. При
Определим пределы интегрирования для переменной z. При  получаем
получаем  , при
, при 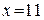 получаем
получаем  .
.
Выразив подынтегральное выражение через z и переходя к новым пределам, получим 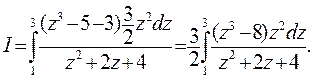
Так как разность кубов  то, сократив на знаменатель, получим
то, сократив на знаменатель, получим
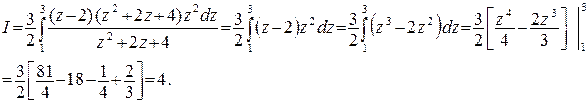
Задача 23.Вычислить интеграл  или установить его расходимость.
или установить его расходимость.
Решение: Подынтегральная функция 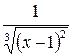 имеет бесконечный разрыв при
имеет бесконечный разрыв при  , т. е. в точке, принадлежащей интервалу интегрирования. Данный интеграл является несобственным. Если подынтегральная функция f(x) интеграла
, т. е. в точке, принадлежащей интервалу интегрирования. Данный интеграл является несобственным. Если подынтегральная функция f(x) интеграла  имеет бесконечный разрыв при х = с, где а<с<b, а во всех других точках отрезка [а,b] непрерывна, то по определению полагают:
имеет бесконечный разрыв при х = с, где а<с<b, а во всех других точках отрезка [а,b] непрерывна, то по определению полагают:
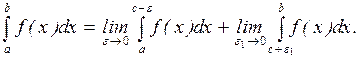 (*)
(*)
Если оба предела в правой части (*) существуют, то интеграл 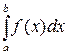 называется сходящимся. Если хотя бы один из указанных пределов не существует, то интеграл
называется сходящимся. Если хотя бы один из указанных пределов не существует, то интеграл 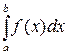 называется расходящимся.
называется расходящимся.
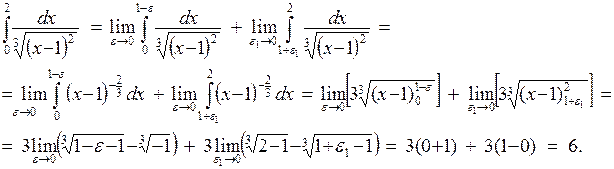
Следовательно, данный интеграл — сходящийся.
Замечание. Равенство (*) можно использовать для каждой отдельной точки разрыва, принадлежащей интервалу (а, b).