рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Теорема (достаточные условия экстремума).
Реферат Курсовая Конспект
Теорема (достаточные условия экстремума).
Теорема (достаточные условия экстремума). - раздел Математика, МАТЕМАТИКА Если ...
- Если
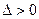 и
и 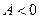 , то
, то 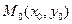 - точка максимума.
- точка максимума. - Если
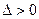 и
и  , то
, то 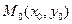 - точка минимума.
- точка минимума. - Если
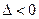 , то
, то 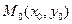 не является точкой экстремума.
не является точкой экстремума.
4. Если 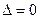 , то точка
, то точка 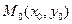 может как быть, так и не быть точкой экстремума,
может как быть, так и не быть точкой экстремума,
2.13).Найти точки экстремума и экстремальные значения функции
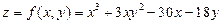 .
.
Найдем частные производные  и
и  . Приравнивая эти производные нулю, получаем систему уравнений
. Приравнивая эти производные нулю, получаем систему уравнений
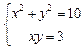
Ее решениями являются следующие четыре стационарные точки: 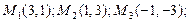
 . Теперь вычислим вторые частные производные данной функции
. Теперь вычислим вторые частные производные данной функции 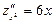 ,
,  ,
,  и составим определитель
и составим определитель  . Найдем значения этого определителя в каждой из полученных стационарных точек:
. Найдем значения этого определителя в каждой из полученных стационарных точек:
1.  . Поэтому
. Поэтому  - точка минимума.
- точка минимума.
2. 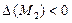 , в точке
, в точке 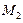 экстремума нет.
экстремума нет.
3. 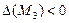 , в точке
, в точке 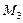 экстремума нет.
экстремума нет.
4.  ,
,  - точка максимума.
- точка максимума.
Подставляя координаты двух экстремальных точек 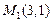 и
и  в данную функцию, получим
в данную функцию, получим  - минимум,
- минимум,  - максимум.
- максимум.
Задания для самостоятельного решения
Найти области определения следующих функций:
2.1.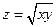 . 2.2.
. 2.2. . 2.3.
. 2.3. 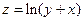 . 2.4.
. 2.4. 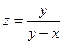 . 2.5.
. 2.5.  .
.
Определить линии уровня и построить некоторые из них при 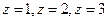 для следующих функций:
для следующих функций:
2.6.  . 2.7.
. 2.7. 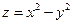 . 2.8.
. 2.8. 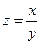 . 2.9.
. 2.9.  . 2.10.
. 2.10. 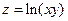 .
.
Найти частные производные следующих функций, записать полный дифференциал:
2.11. 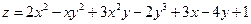 . 2.12.
. 2.12.  . 2.13.
. 2.13. 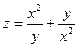 .
.
2.14. 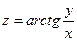 . 2.15.
. 2.15. 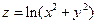 . 2.16.
. 2.16.  . 2.17.
. 2.17. 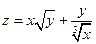 .
.
2.18. 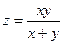 . 2.19.
. 2.19. 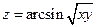 .
.
Найти частные производные второго порядка.
2.20. 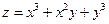 . 2.21.
. 2.21. . .2.22.
. .2.22. 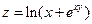 . 2.23.
. 2.23.  .
.
2.24. Вычислить производную функции  в точке
в точке  по направлению вектора
по направлению вектора  .
.
2.25. Найти производную функции 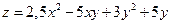 в точке
в точке  в направлении, составляющем с осью
в направлении, составляющем с осью 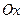 угол
угол  . Определить направление максимального роста данной функции в данной точке.
. Определить направление максимального роста данной функции в данной точке.
2.26. Найти направление максимального роста функции  в точке
в точке  .
.
2.27. Найти производную по направлению биссектрисы первого координатного угла в точке 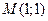 функции
функции  .
.
2.28. Найти градиент функции 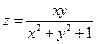 в точке
в точке 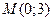 .
.
Исследовать на экстремум следующие функции:
2.29. 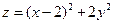 . 2.30.
. 2.30.  . 2.31.
. 2.31. 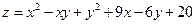 .
.
2.32.  . 2.33.
. 2.33. 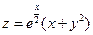 . 2.34.
. 2.34. 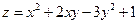 .
.
Ответы:
2.1.  . 2.2.
. 2.2.  . 2.3.
. 2.3. 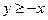 . 2.4.
. 2.4.  и
и 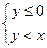 . 2.5.
. 2.5. 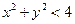 .
.
2.6.  . 2.7.
. 2.7. 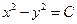 . 2.8.
. 2.8.  . 2.9.
. 2.9.  . 2.10.
. 2.10.  .
.
2.11.  . 2.12.
. 2.12.  .
.
2.13.  . 2.14.
. 2.14.  .
.
2.15. 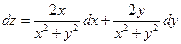 . 2.16.
. 2.16. 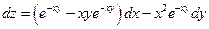 .
.
2.17. 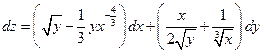 . 2.18.
. 2.18.  .
.
2.19.  . 2.20.
. 2.20. 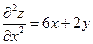 ,
, 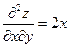 ,
,  .
.
2.21. 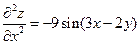 ,
,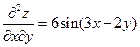 ,
, .
.
2.22.  ,
, 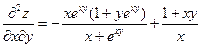 ,
,
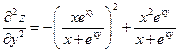 .
.
2.23.  ,
,  ,
, 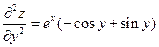 .
.
2.24.. 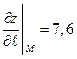 . 2.25.
. 2.25.  ,
, 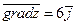 . 2. 26.
. 2. 26.  . 2.27.
. 2.27.  .
.
2.28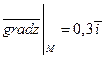 . 2.29.
. 2.29. 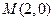 - точка минимума. 2.30. Точек экстремума нет.
- точка минимума. 2.30. Точек экстремума нет.
2.31. 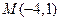 - точка минимума. 2.32.
- точка минимума. 2.32.  - точка максимума.
- точка максимума.
2.33.  - точка минимума. 2.34. Точек экстремума нет.
- точка минимума. 2.34. Точек экстремума нет.
Контрольная работа № 2.Функции нескольких переменных.
1. Найти область определения функции и изобразить ее на плоскости 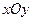 .
.
2. Определить линии уровня функции, изобразить некоторые из них при 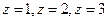 .
.
3. Найти частные производные 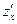 ,
,  данной функции, записать ее полный дифференциал.
данной функции, записать ее полный дифференциал.
4. Вычислить частные производные второго порядка.
5. Вычислить градиент и производную функции в данной точке 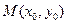 по направлению
по направлению 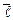 .
.
6. Исследовать функцию на экстремум. Определить точки максимума и минимума, вычислить максимальные и минимальные значения данной функции.
Вариант 1.
1.  . 2.
. 2.  . 3.
. 3. 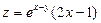 . 4.
. 4. 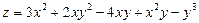 .
.
5.  . 6.
. 6.  .
.
Вариант 2.
1.  . 2.
. 2. 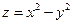 . 3.
. 3. 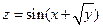 . 4.
. 4. 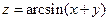 .
.
5. 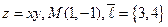 . 6.
. 6. 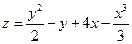 .
.
Вариант 3.
1. 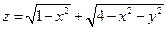 . 2.
. 2. 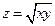 . 3.
. 3. 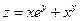 . 4.
. 4. 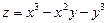 .
.
5.  . 6.
. 6. 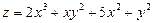 .
.
Вариант 4.
1.  . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 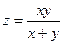 .
.
5.  . 6.
. 6. 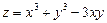 .
.
Вариант 5.
1. 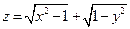 . 2.
. 2.  . 3.
. 3. 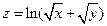 . 4.
. 4. 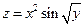 .
.
5.  . 6.
. 6.  .
.
Вариант 6.
1. 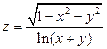 . 2.
. 2. 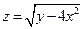 . 3.
. 3.  . 4.
. 4.  .
.
5. . 6.
. 6. 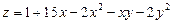 .
.
Вариант 7.
1.  . 2.
. 2. 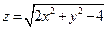 . 3.
. 3. 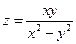 . 4.
. 4. 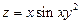 .
.
5. 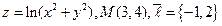 . 6.
. 6.  .
.
Вариант 8.
1. 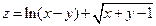 . 2.
. 2. 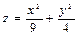 . 3.
. 3. 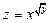 . 4.
. 4. 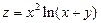 .
.
5.  . 6.
. 6.  .
.
Вариант 9.
1.  . 2.
. 2. 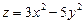 . 3.
. 3.  . 4.
. 4.  .
.
5. 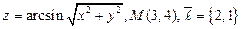 . 6.
. 6. 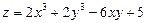 .
.
Вариант 10.
1. 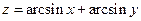 . 2.
. 2. 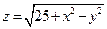 . 3.
. 3. 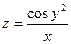 . 4.
. 4. 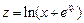 .
.
5.  . 6.
. 6.  .
.
Вариант 11.
1. 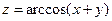 . 2.
. 2.  . 3.
. 3.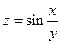 . 4.
. 4.  .
.
5. 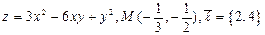 . 6.
. 6.  .
.
Вариант 12.
1. 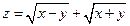 . 2.
. 2. 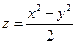 . 3.
. 3. 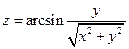 . 4.
. 4. 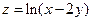 .
.
5.  . 6.
. 6.  .
.
Вариант 13.
1. 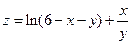 . 2.
. 2.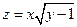 . 3.
. 3. 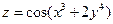 . 4.
. 4.  .
.
5. 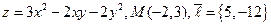 . 6.
. 6. 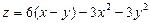 .
.
Вариант 14.
1. 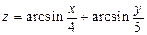 . 2.
. 2. 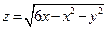 . 3.
. 3. 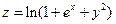 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
Вариант 15.
1. 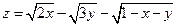 . 2.
. 2.  . 3.
. 3. 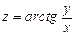 . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
Вариант 16.
1. 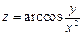 . 2.
. 2.  . 3.
. 3.  . 4.
. 4. 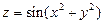 .
.
5.  . 6.
. 6. 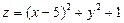 .
.
Вариант 17.
1.  . 2.
. 2. 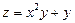 . 3.
. 3.  . 4.
. 4. 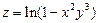 .
.
5. 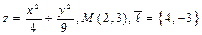 . 6.
. 6. 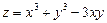 .
.
Вариант 18.
1.  . 2.
. 2. 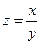 . 3.
. 3.  . 4.
. 4.  .
.
5. 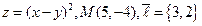 . 6.
. 6.  .
.
Вариант 19.
1. 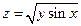 . 2.
. 2. 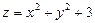 . 3.
. 3. 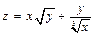 . 4.
. 4. 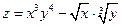 .
.
5. 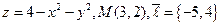 . 6.
. 6. 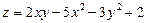 .
.
Вариант 20.
1. 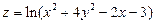 . 2.
. 2. 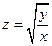 . 3.
. 3. 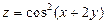 . 4.
. 4.  .
.
5. 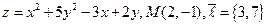 . 6.
. 6. 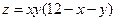 .
.
Вариант 21.
1.  . 2.
. 2.  . 3.
. 3. 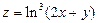 . 4.
. 4. 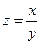 .
.
5. 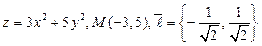 . 6.
. 6. 
Вариант 22.
1.  . 2.
. 2.  . 3.
. 3. 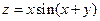 . 4.
. 4. 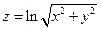 .
.
5. 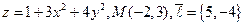 . 6.
. 6. 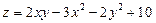 .
.
Вариант 23.
1. 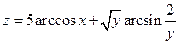 . 2.
. 2.  . 3.
. 3. 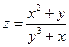 . 4.
. 4. 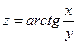 .
.
5. 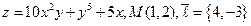 . 6.
. 6. 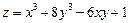 .
.
Вариант 24.
1. 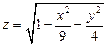 . 2.
. 2.  . 3.
. 3. 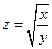 . 4.
. 4.  .
.
5.  . 6.
. 6. 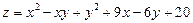 .
.
Вариант 25.
1. 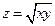 . 2.
. 2.  . 3.
. 3.  . 4.
. 4.  .
.
5. 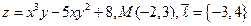 . 6.
. 6.  .
.
Вариант 26.
1.  . 2.
. 2. 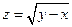 . 3.
. 3.  . 4.
. 4.  .
.
5. 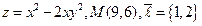 . 6.
. 6. 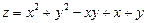 .
.
Вариант 27.
1. 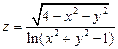 . 2.
. 2. 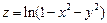 . 3.
. 3. 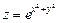 . 4.
. 4. 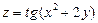 .
.
5. 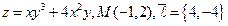 . 6.
. 6.  .
.
Вариант 28.
1. 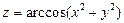 . 2.
. 2.  . 3.
. 3. 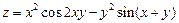 . 4.
. 4. 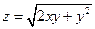 .
.
5. 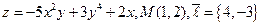 . 6.
. 6. 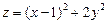 .
.
Вариант 29.
1. 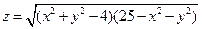 . 2.
. 2.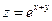 . 3.
. 3.  . 4.
. 4. 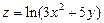 .
.
5. 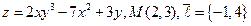 . 6.
. 6. 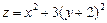
Вариант 30.
1. 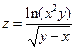 . 2.
. 2. 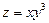 . 3.
. 3. 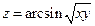 . 4.
. 4. 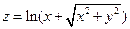 .
.
5.  . 6.
. 6. 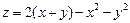 .
.
3. Дифференциальные уравнения
3.1.Общие понятия
Уравнения, в которых неизвестная функция входит под знаком производной или дифференциала, называются дифференциальными уравнениями.
Если неизвестная функция зависит только от одного аргумента – одной независимой переменной, то дифференциальное уравнение называется обыкновенным, а если она зависит от нескольких аргументов и дифференциальное уравнение содержит какие - либо ее частные производные по этим аргументам, то оно называется дифференциальным уравнением с частными производными.
Порядком дифференциального уравнения называется наивысший порядок содержащейся в этом уравнении производной искомой функции. Например, уравнение 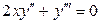 , где
, где  – независимая переменная, а
– независимая переменная, а  – искомая функция, является обыкновенным дифференциальным уравнением третьего порядка. Уравнение
– искомая функция, является обыкновенным дифференциальным уравнением третьего порядка. Уравнение 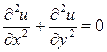 , в котором
, в котором  и
и 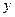 – две независимые переменные, а
– две независимые переменные, а 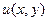 - искомая функция этих переменных, является дифференциальным уравнением с частными производными второго порядка.
- искомая функция этих переменных, является дифференциальным уравнением с частными производными второго порядка.
В настоящих методических указаниях рассматриваются некоторые из основных методов решения обыкновенных дифференциальных уравнений.
– Конец работы –
Эта тема принадлежит разделу:
МАТЕМАТИКА
Федеральное государственное образовательное бюджетное... учреждение высшего профессионального образования... Московский технический университет связи и информатики...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теорема (достаточные условия экстремума).
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов