Интегрирование по частям.
Если 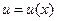 и
и 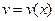 - непрерывно дифференцируемые функции, то, поскольку
- непрерывно дифференцируемые функции, то, поскольку 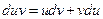 , справедлива следующая формула
, справедлива следующая формула 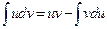 , использование которой называют интегрированием по частям.
, использование которой называют интегрированием по частям.
11.11). 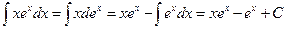 . Здесь
. Здесь 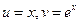 .
.
1.12).  =
=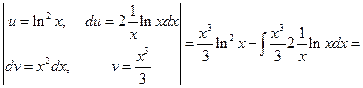
 .
.
Последний интеграл вычислим отдельно вторично применяя интегрирование по частям.
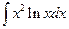
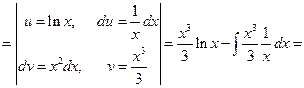
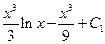 . Итак, окончательно
. Итак, окончательно
получаем 
 .
.
Задания для самостоятельного решения
1.1.  . 1.8.
. 1.8. 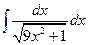 . 1.15.
. 1.15.  . 1.22.
. 1.22. .
.
1.2. 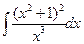 . 1.9.
. 1.9. 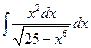 . 1.16.
. 1.16. 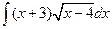 . 1.23.
. 1.23.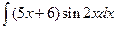 .
.
1.3. 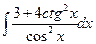 . 1.10.
. 1.10.  . 1.17.
. 1.17. 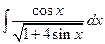 . 1.24.
. 1.24. 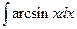 .
.
1.4.  . 1.11.
. 1.11.  . 1.18.
. 1.18. 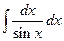 . 1.25.
. 1.25. 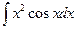 .
.
1.5. 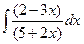 . 1.12.
. 1.12. 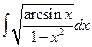 . 1.19.
. 1.19.  . 1.26.
. 1.26.  .
.
1.6. 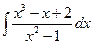 . 1.13.
. 1.13.  . 1.20.
. 1.20. 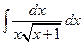 . 1.27.
. 1.27. 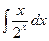 .
.
1.7.  . 1.14.
. 1.14. 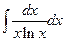 . 1.21.
. 1.21. 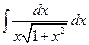 . 1.28.
. 1.28. 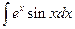 .
.
Ответы:
1.1. . 1.8.
. 1.8.  . 1.15.
. 1.15. 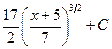 . 1.22.
. 1.22.  .
.
1.2.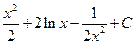 .1.9.
.1.9. 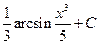 . 1.16.
. 1.16.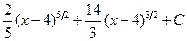 . 1.23.
. 1.23. .
.
1.3.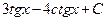 . 1.10.
. 1.10.  . 1.17.
. 1.17. 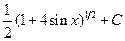 . 1.24.
. 1.24.  .
.
1.4.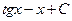 . 1.11.
. 1.11.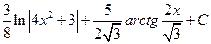 . 1.18.
. 1.18. .
.
1.25.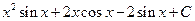 .
.
1.5.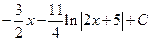 .1.12.
.1.12.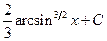 . 1.19.
. 1.19.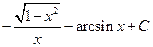 . 1.26.
. 1.26.
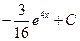 .
.
1.6.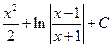 . 1.13.
. 1.13.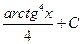 . 1.20.
. 1.20.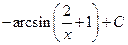 . 1.27.
. 1.27. 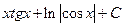 .
.
1.7.  . 1.14.
. 1.14.  . 1.21.
. 1.21.  . 1.28.
. 1.28.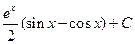 .
.