Интегрирование рациональных выражений
Рассмотрим интеграл от рациональной дроби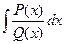 
, в которой степень многочлена 
в числителе не меньше степени многочлена 
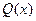в знаменателе. Деление с остатком числителя на знаменатель позволяет представить эту подынтегральную функцию в виде суммы многочлена, как целой части данной неправильной рациональной дроби, и некоторой правильной рациональной дроби 
(степень многочлена 
меньше степени многочлена ).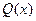
1.13).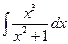
. Подынтегральная функция здесь - это неправильная рациональная дробь.
Деление с остатком (“деление в столбик”) позволяет выделить ее целую часть и представить в виде: 
. А исходный интеграл вычисляется как разность двух интегралов.
.
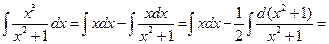
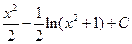Из курса алгебры известна следующая
Теорема. Любая правильная рациональная дробь может быть представлена в виде суммы простейших дробей вида
,
где 
; 
.
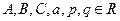1.14). 
. В соответствии с разложением знаменателя данной рациональной дроби по корням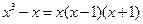 
сама дробь по сформулированной выше Теореме представляется в виде суммы простейших дробей первого типа
.
Умножая обе части этого равенства на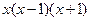 
, получим
.
Это равенство двух многочленов выполняется тождественно для всех 
, а это возможно только при совпадении коэффициентов при одинаковых степенях 
.
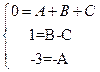
Решая эту систему трех линейных уравнений с тремя неизвестными, получаем 
, 
,
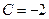. Таким образом, подынтегральная функция представляется в виде
,
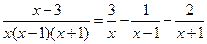поэтому
.
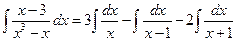
1.15).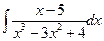 
. Поскольку многочлен третьей степени в знаменателе данной правильной дроби обращается в нуль при 
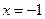, остальные его корни находим делением этого многочлена на 
, и получаем следующее разложение знаменателя дроби по корням
,
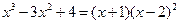в соответствии с которым по той же Теореме записываем представление подынтегральной функции в виде
.
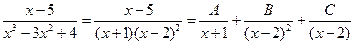В этом представлении множителю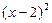 
соответствуют две дроби второго и первого типа. Умножая обе части этого равенства на 
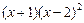, т.е. освобождаясь от знаменателей, получим равенство двух многочленов 
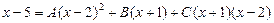. Составить систему
для определения коэффициентов 
можно двумя способами: приравнять коэффициенты при одинаковых степенях , или подставить в равенство многочленов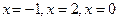 
. Итак, получаем 
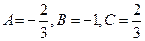. Следовательно,
.
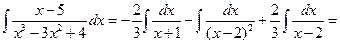
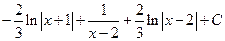1.16).
. Разложение знаменателя по корням
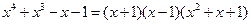определяет представление подынтегральной функции в виде суммы простейших дробей первого и третьего типов
.
Коэффициенты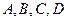 
находим из тождества
,
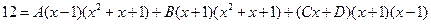в которое подставляем четыре различных значения 
. Отсюда система
,
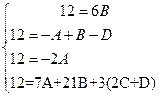имеющая решение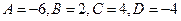 
. Таким образом, исходный интеграл представлен в виде суммы следующих интегралов:
.
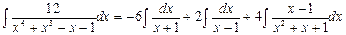Последний интеграл в правой части равенства вычислим выделяя в числителе производную
знаменателя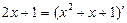 
и выделяя полный квадрат в знаменателе второго из следующих интегралов:
.
Окончательный ответ выглядит так
.
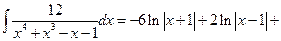
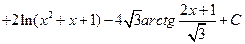Замечание. При вычислении интеграла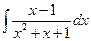
были продемонстрированы два основных приема, используемых для интегрирования функций, содержащих квадратный трехчлен, например, интегралов от простейших дробей третьего типа: 
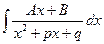. А именно: выделение в числителе производной знаменателяи выделение полного квадрата в знаменателе. В том случае, когда квадратный трехчлен в знаменателе имеет действительные корни, следует пользоваться тем, что подынтегральная функция разлагается на две простейшие дроби первого типа.