рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.

Реферат Курсовая Конспект

Выберите учебное заведение

Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.

Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница. - раздел Математика, МАТЕМАТИКА Пусть Функция ...

Пусть функция 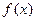интегрируема на , , . Тогда функция

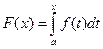называется интегралом с переменным верхним пределом. Перечислим основные его свойства.

1. Если 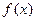интегрируема на , то функция 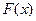непрерывна для любого .

2. Если 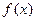непрерывна в точке 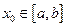, то функция 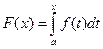имеет производную в этой точке, и 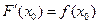. Поэтому всякая непрерывная функция имеет первообразную.

3. Если 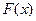- какая-нибудь первообразная непрерывной на отрезке функции 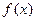, то справедливо равенство

называемое формулой Ньютона – Лейбница.

1.24). 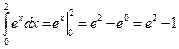. 1.25). .

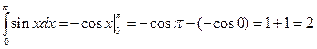1.26). .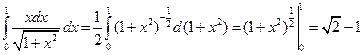

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

МАТЕМАТИКА

Федеральное государственное образовательное бюджетное... учреждение высшего профессионального образования... Московский технический университет связи и информатики...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Интеграл с переменным верхним пределом. Формула Ньютона – Лейбница.

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Второй семестр
УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС для бакалавров по специальностям: 080100, 080200, 230700, 010300 Москва 2012 УДК 5

Разложение подынтегральной функции на слагаемые.
Представляя подынтегральную функцию в виде алгебраической суммы отдельных слагаемых, можно воспользоваться свойством IV и проинтегрировать каждое слагаемое отдельно, используя в дал

Метод подстановки.
Упрощение интеграла достигается введением новой независимой переменной

Интегрирование по частям.
Если и -

Интегрирование рациональных выражений
Рассмотрим интеграл от рациональной дроби , в которой степень многочлена

Интегрирование простейших иррациональностей
Интегралы вида , где подынтегральная функция рациональна относительно переменной интегрирования

Интегрирование тригонометрических функций
Интегралы вида рационализируются универсальной тригонометрической подстановкой:

Свойства определенного интеграла.
1. (). 2.

Замена переменной в определенном интеграле.
Допустим, что в процессе вычисления определенного интеграла производится замена переменной:

Вычисление площади плоских фигур.
Используя геометрический смысл определенного интеграла, вычисляется площадь фигуры, ограниченной графиками функций

Теорема (необходимый признак существования экстремума).
Если - точка экстремума (максимума, или минимума) функции

Теорема (достаточные условия экстремума).
Если и

Теорема о существовании и единственности решения Задачи Коши (3.2),(3.4).
Если в уравнении (3.2) функция и ее частная производная

Признак Лейбница сходимости знакочередующегося ряда.
Знакочередующийся ряд сходится, если выполнены следующие два условия: абсолютные значения его членов представляют собой убывающую последовательность