КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ По разделу «УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ. »

-.

КРАТКИЙ КОНСПЕКТ ЛЕКЦИЙ

По разделу

«УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ. »

Курса СПЕЦИАЛЬНЫЕ ГЛАВЫ ВЫСШЕЙ МАТЕМАТИКИ.

( IV семестр, II курс, поток 3ПТК-6, 3МПТ-8 2012 г)

Лекция 1. Основные понятия и определения дифференциальных уравнений с частными производными (ДУрЧП).

Понятия о функциональных ДУрЧП. Основные определения (порядок, линейность, область определения).

(1)  

Порядок.Линейность.

Если функциональное выражение содержит искомуюфункцию ивсе еепроизводные в первой степени,то УрЧП- линейное, в противном случае– нелинейное.

Канонические формы УрЧП второго порядка

-параболические  

Общее решение УрЧП.

Всякое УрЧП имеет бесконечное множесто линейно независимых частных решений (классических решений-интегралов), удовлетворяющих определенным (классическим) условиям

- непрерывности вместе со старшей производной ;

(15)

- дифференцируемости до 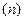-го порядка ;

- удовлетворять уравнению(превращает их в тождество);

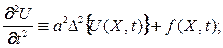
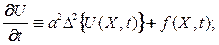
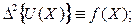(16)

- непрерывныпри подходек граничным 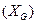и начальнымточкам области определения;

 

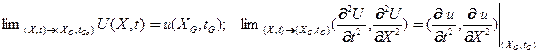
- представимости обобщенного решения в виде ряда по «классическим решениям»

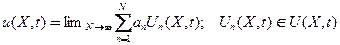(17)

Частное решение УрЧП.

Всякое решениеудовлетворяющеедополнительным (начальным и краевых-граничным) условиям –частное решениеначально-краевой (граничной) задачи.Это частное решение превращает их втожлествоне толькоуравнение(16),но иначально-краевые условия

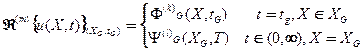(18)

 

т.е. тождества

(19)

 

называется частным решением начально-краевой задачи.

 

1.6. Постановка начально-краевой задачи для УрЧП порядка 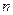: Найти такую непрерывную 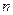раз дифференцируемую функцию 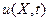, превращающую уравнение(16)в области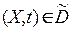и начально-краевые условия (18) на границе области 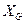и в начальный момент времени в тождества. Для уравнений второго порядка , содержащих вторую производную по времени два «временных» начальных условия , а для уравнений содержащих только первую производную по времени –одно (первое) условие

-для искомой функции

 

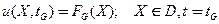(20)

 

--для ее первой производной (скорости)

(21)

а краевых (граничных) различают три типа линейных условий:

- первого рода (Дирихле) -заданы значенияискомойфункции на границе

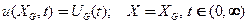(22)

 

-второго рода (Неймана) -задана производная по нормали 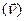к контуру 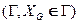, ограничивающему область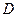

 

(23)

 

-третьего рода (Робина – Ньютона)(G.Robin 1886-I.Newton 1687) – задана линейная комбинацияискомойфункциии еепроизводной по нормали 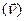к контуру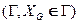, ограничивающему область

 

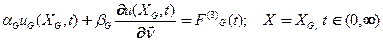(24)

 

Уравнения в частных производных первого порядка с двумя независимыми переменными.

2.1.Геометрическая интерпретация УрЧП первого порядка. Любая поверхность, проходящая через точку 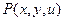с координатами 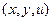, имеет касательную плоскость, положение которой определяется величинами 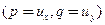, удовлетворяющими уравнению

 

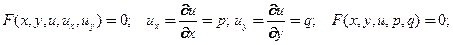(25)

 

т.е. образуют параметрическое семейство возможных касательных плоскостей, проходящих через прямую-«ось Монжа», а в качестве огибающейэтого семейства-«конус Монжа»(Монж Г.-G.Monge 1795). Поэтому УрЧП первого порядка – это «поле конусов» или поле направлений.Функция 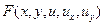непрерывнавместе с первой производной по всем аргументами, кроме того, удовлетворяет условию

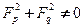(26)

 

Сведение УрЧП к системе ОДУ. Конус и кривая (фокальная) Монжа.

  (27)

Лекция 2. УрЧП второго порядка,. Уравнения гиперболического (волнового) типа.

Задачи, приводяшиеся к гиперболическим УрЧП.

Уравнения поперечных колебаний длинной струны.

Струна: тонкая, абсолютно гибкая, не имеет сопротивления на изгиб-внутренняя реакция имеет только одну продольную силу натяжения 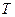, направленную по касательной к струне, нерастяжима, однородная, постоянного поперечного единичного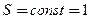сечения, погонной плотности 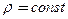, длина значительно больше поперечного размера .

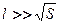Колебания малые: отклонения от положения равновесия малые такие,

что

 

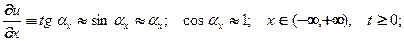(1)

 

происходят в одной плоскости и в каждый момент времени находятся на одной прямой, перпендикулярной продольной оси.

Уравнения:

Закон Ньютона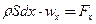

Кинематические соотношения – ускорение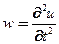

Уравнения равновесияна поперечной прямой (отсуствие движения вдоль оси) –проекция на поперечную () и движения в поперечном направлении ().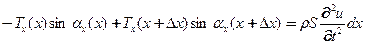

Следствия уравнений равновесия: натяжение постоянно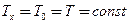, а

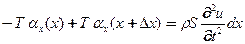
или с учетом (1) имеем уравнения свободных поперечных колебаний струны

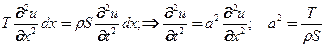(2)

 

Добавляя в правую часть действие внешних сил 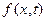и сил сопротивления вязкого и упругого имеем уравнения вынужденных поперечных колебаний струны (одномерные) в среде с сопротивлением

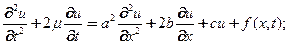(3)

 

Аналогично представляется уравнение поперечные колебания мембраны (двумерные)

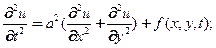
или через дифференциальный оператор Лапласа в правой части

 

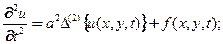(4)

2.1.2. Продольные колебания стержня.

Стержень: цилиндрическое (призматическое) тело постоянного поперечного 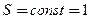сечения, однородное плотности 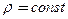, длина значительно больше поперечного размера 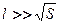, линейно упругий (по Гуку)(Гук Р.-R.Hooke 1660).

Колебания малые: продольные отклонения от положения равновесия малые такие, что деформации, испытываемые стержнем малые (по Коши)(Коши О.Л.-A.L.Cauchy -1846 )

 

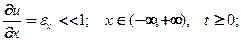(5)

 

происходят в одной плоскости и в каждый момент времени находятся на одной прямой- на продольной оси.

Уравнения:

Закон Ньютона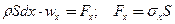

Закон Гука «нормальные напряжение – продольная деформация» 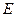-модуль Юнга.

Кинематические соотношения – ускорение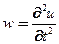

Уравнения движения: в проекции на продольную ось

 

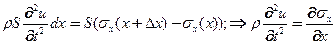(6)

 

или после подстановки закона Гука имеем уравнения продольных свободных колебаний стержня

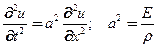(7)

 

и с учетом внешних сил 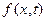и сил сопротивления вязкого и упругого имеем уравнения вынужденных продольных колебаний стержня в среде с сопротивлением

 

 

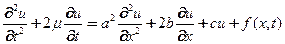(8)

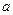- скорость продольных волн (скорость звука).

 

2.1.3.Крутильные колебания вала.

Вал: цилиндрическое круглое тело постоянного поперечного 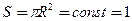сечения, однородное плотности 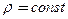, длина значительно больше поперечного размера , линейно упругий (по Гуку).

Колебания малые: малые углы крутки 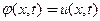отклонения от положения равновесия такие, что деформации, испытываемые стержнем малые (по Коши)

 

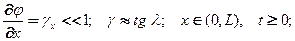(9)

 

происходят в одной плоскости, перпедикулярной оси кручения и в каждый момент времени находятся в этой плоскости.

Гипотеза плоских сечений Сен-Венана(Барре де Сен-Венан А.Ж.К.-A.J.C.Barre de Seint-Venant 1845): сечения остаются плоскими, а радиусы прямолинейными

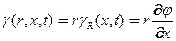(10)

 

Уравнения:

Закон Ньютона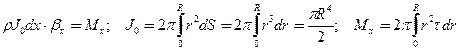

Закон Гука «касательные напряжения – сдвиговая деформация» 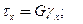-модуль сдвига.

Кинематические соотношения – угловое ускорение

Уравнение движения (вращения относительно оси)

 

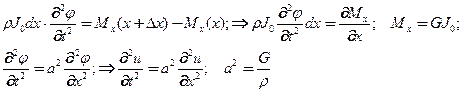(11)

 

или с учетов внешних крутящих моментов и моментов вязкого и упругого сопротивления

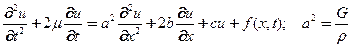(12)

 

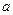- скорость сдвиговых волн.

 

2.1.4. Телеграфное уравнение (электрические колебания в однородной длинной цепи).Двухпроводная система (линия) напряжение между ними , а ток

 

имеет активное сопротивление 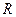, индуктивность , емкость 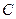и активную проводимость .

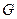Законы электрических цепей:

Закон Ома (Ом Г.-GS..Ohm 1832)для участка 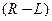цепи и закон взаимной электрической индукции Ленца(Ленц Э.Х.-E.Ch.Lenz 1832)

 

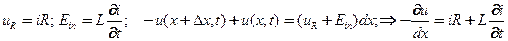(13)

 

Закон Кирхгоффа (Кирхгоф Г.Р.-G.R.Kirchhof 1864) для цепи 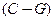и закон накопления заряда и потерь

 

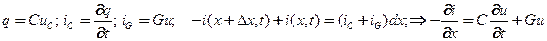(14)

 

Исключая одну из искомых величин имеем телеграфное уравнение относительно напряжения

 

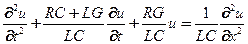(15)

 

или относительно силы тока

 

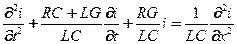(16)

 

2.1.5. Уравнения Максвелла.Оператор Д’Аламбера.

Скалярный электрический потенциал 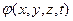и векторный магнитный 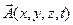потенциал связаны системой уравнений Максвелла(Максвелл Д.К.-J.Cl.Maxwell -1863)

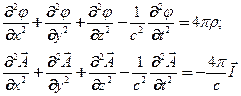(17)

 

Используя дифференциальный оператор Д’Аламбера(Даламбер Ж.Л. J.L.D‘Alambert 1754)

 

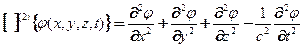
эта система принимает вид

 

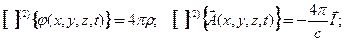(18)

 

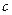- скорость света.

 

2.2.Постановка начально-краевой залачидля гиперболических двумерныз УрЧП.

Частное решениеУрЧП опредеяется заданием дополнительных условий

- начальных:

начальное положение

 

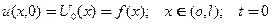(19)

 

начальная скорость

 

(20)

 

- краевых (граничных):

на левой границе

 

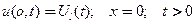(21)

 

на правой границе

 

(22)

 

Постановка задачи: Найти решение ( в классе дважды дифференцирумых по обеим переменным функций) УрЧП второго порядка с постоянными коэффициентами

 

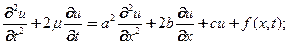(23)

 

при начальных условиях

 

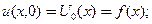
(24)

 

и граничных условиях

 

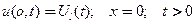
(25)

2.2.1.Колебание бесконечной струны. Формула Д’Аламбера

Струна бесконечной протяженности – ни какие граничные условия не накладываются, кроме ограниченности: найти решение начальной задачи для УрЧП

 

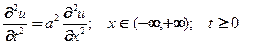(26)

 

с начальными условиями

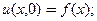
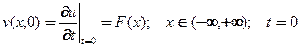(27)

 

Метод решения: замены переменных

 

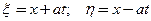(28)

 

редуцированное уравнение и его решение

 

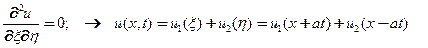(29)

 

после подстановки в начальные условия м мнтегрирования имеем решение в виде суммы двух бегущих волн

 

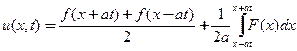(30)

 

решение Д’Аламбера задачи Коши дляУрЧП колебанияструны.

Распространение отклонений.

Прямая волна –вправо, обратная волна -влево: передний и задний фронт волны. Фазовая плоскость и семейство ()- линий – характеристик.

Распространение импульсов.

Прямая волна –вправо, обратная волна -влево: передний и задний фронт волны. Фазовая плоскость и семейство ()- линий – характеристик. 2.3.Метод разделения переменных Фурьерешения начально-краевых задач для гиперболических УрЧП.

Метод разделения переменных

 

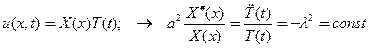(32)

 

Редуцированная система начальной и краевой задач для ОДУ

 

(33)

 

и ее решения (относительно 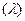– задача на собственные значения Штурма-Лиувилля) (Штурм Ж.Ш.Ф.-J.Ch.F.Sturm 1840 ,Лиувилль Ж. – J.Liouville 1856)

 

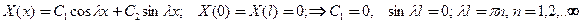
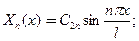(34)

собственные функции 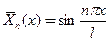(счетное множество) удовлетворяют однородным краевым условиям для каждого значения 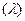.Вторая системафукций определяется как общее решение

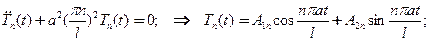(35)

 

произвольные постоянные интегрирования определяются из начальных условий после подстановки этих решений в выражение для искомой функции

 

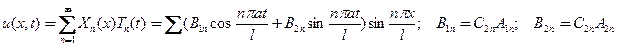(36)

 

Разлагая начальные функции в ряд Фурье(Фурье Ж.Б.Ж.-J.B.J.Fourier 1816) по нечетным функциям

 

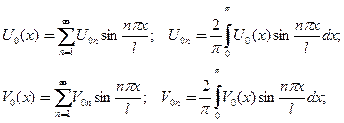(37)

 

и приравнивая их значения имеем

 

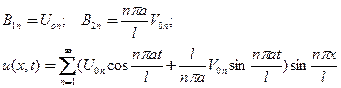(38)

 

Получили решение в виде одинарного функционального ряда по временной и пространственной переменным.

 

 

Лекция 3. Гиперболические УрЧП. Метод Фурье (продолжение).

3.1. Начально-краевая задача с неоднородной правой частью и однородными краевыми условиями. Постановка задачи включает УрЧП с неоднородной правой частью, разложимой в ряд Фурье

 

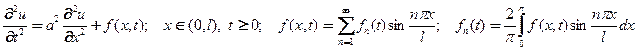(1)

 

начальные условия (неоднородные), разложимые в ряд Фурье

(2)

 

однородные краевые условия

 

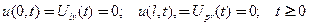(3)

 

Решение задается в форме ряда Фурье

 

(4)

 

уловлетворяет“автоматически” краевым условиям, а составляющие удовлетворят ОДУ второго порядка с постоянными коэффициентами и комплексно-сопряженными характеристическими показателями

 

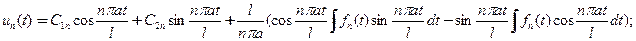(5)

 

постоянные интегрирования определяются из (оставшихся) начальных условий

 

(6)

 

что дает для коэффициентов ряда Фурье значения

 

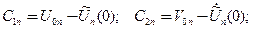
и окончательно для решения выражение в виде

 

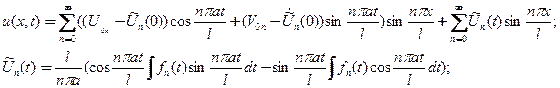(7)

 

3.2. Начально-краевая задача с неоднородной правой частью и неоднородными краевыми условиями. Постановка задачи включает УрЧП с неоднородной правой частью, разложимой в ряд Фурье

 

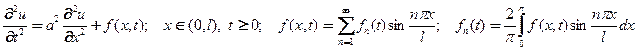(8)

 

начальные условия (неоднородные), разложимые в ряд Фурье

(9)

 

Неоднородные краевые условия,

  Введениемновой искомой функции (11)

Однородные краевые условия,

Решение задается в форме ряда Фурье   (15)

Разложение по окружной координате

  приводит к системам уравнений : -при

Уравнения в частных производных параболического типа.

Уравнение распространения тепла стержне.

Стержень:тонкий (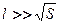), призматический, однородный, постоянного поперечного 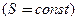сечения, плотности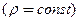, теплоемкости, теплоизолирован по боковым поверхностям.

 

Законы теплопроводности:

Закон сохранения (баланса) тепла – тепло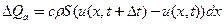, аккумулированное массой 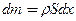в обьеме 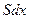при изменении 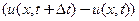температуры равно теплупритекшему через границы от соседних частиц (тепловой поток)

 

(30)

 

Закон теплопередачи Фурье через граничные поверхности: тепловой поток пропорционален градиенту температуры с коэффициентом теплопередачи )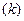

 

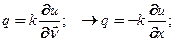(31)

 

В результате имеем УрЧП теплопроводности стержня

 

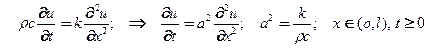(32)

здесь– коэффициент температуропроводности.

 

Уравнение диффузии (фильтрации) в капиляре-трубке.

Капиляр:тонкий (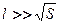), призматический, однородный, постоянного поперечного 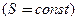сечения, наполнен однородной жидкостью или газом постоянной плотности и пористости , массоизолирован по боковым поверхностям.

 

Законы диффузии:

Закон сохранения (баланса) массы – масса диффундирующего вещества 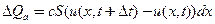, аккумулированное в обьеме 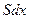при изменении 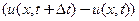концентрации равно массе притекшей через границы от соседних частиц (массовый поток)

 

 

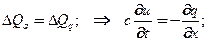
Закон диффузии (фильтрации) Нернста-Дарси(Нернст ВФ.Г..-WFH.Nernst 1890) через граничные поверхности: массовый поток пропорционален градиенту концентрации с коэффициентом массопередачи )

 

 

В результате имеем УрЧП диффузии в капиляре

 

 

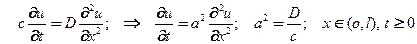
здесь 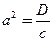– коэффициент массопроводности.

Уравнение диффузии совпадает с уравнением теплопроводности и описывает различные химические реакции (например, эманации радия).

Для двухмерных тел в декартовой стистеме координат УрЧП теплопроводности записывается в виде

 

(33)

 

Для трехмерных тел в декартовой стистеме координат УрЧП теплопроводности записывается в виде

 

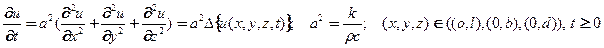(34)

 

4.2. Начальное и краевые условия.

Частное решение УрЧП двух переменных параболического типа , заданное своими постоянными коэффициентами 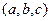и правой частью 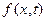в области изменения переменных

 

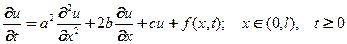(35)

 

определяется дополнительными начально-краевыми условиями:

- начальное условие(одно, т.к. по временной переменной порядок УрЧп - первый)

 

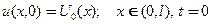(36)

 

-краевые условия (два, т.к. по пространственной переменной порядок УрЧП – второй и задан интервал этой переменной, включая две крайние – граничные точки). Раличаю три типа краевых условий:

Первого рода (Дирихле)

(37)

 

Второго рода (Неймана)

 

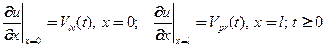(38)

 

Третьего рода (Робина)

 

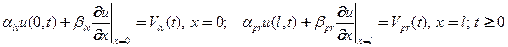(39)

 

Теплопроводность бесконечного стержня. Метод Фурье, Интеграл Фурье.

Бесконечный стержень – влияние краев не сказывается. Задача содержит только начальное условие, а краевые отсуствуют,кроме ограниченности искомой…   (40)

Метод разделения переменных

 

(49)

 

Редуцированная система начальной и краевой задач для ОДУ

 

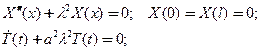(50)

 

и ее решения (относительно 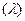– задача на собственные значения Штурма-Лиувилля) (Штурм Ж.Ш.Ф.-J.Ch.F.Sturm 1840 ,Лиувилль Ж. – J.Liouville 1856)

 

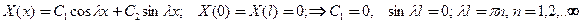
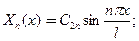(51)

собственные функции 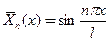(счетное множество) удовлетворяют однородным краевым условиям для каждого значения 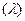.Вторая системафункций определяется как общее решение

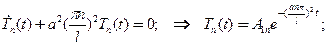(52)

 

произвольные постоянные интегрирования определяются из начальных условий после подстановки этих решений в выражение для искомой функции

 

 

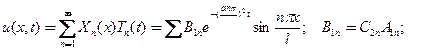(53)

 

Разлагая начальную функцию в ряд Фурье(Фурье Ж.Б.Ж.-J.B.J.Fourier 1816) по нечетным функциям

 

(54)

 

и приравнивая их значения имеем

 

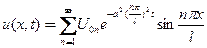(55)

 

Получили решение в виде одинарного функционального ряда по временной и пространственной переменным.

 

 

Лекция 5. Параболические УрЧП. Метод Фурье (продолжение).

5.1. Начально-краевая задача с неоднородной правой частью и однородными краевыми условиями. Постановка задачи включает УрЧП с неоднородной правой частью, разложимой в ряд Фурье

 

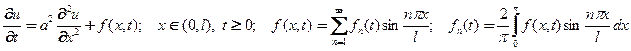(1)

 

начальные условия (неоднородные), разложимые в ряд Фурье

(2)

 

однородные краевые условия

 

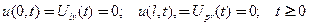(3)

 

Решение задается в форме ряда Фурье

 

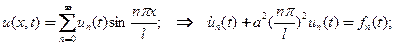(4)

 

уловлетворяет“автоматически” краевым условиям, а составляющие удовлетворят ОДУ первого порядка с постоянными коэффициентами и действительным характеристическим показателем

 

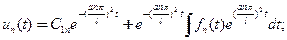(5)

 

постоянную интегрирования определяются из (оставшегося) начального условия

 

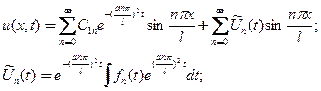(6)

 

что дает для коэффициентов ряда Фурье значения

 

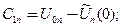
и окончательно для решения выражение в виде

 

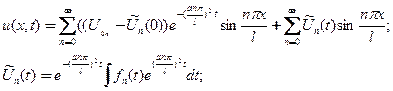(7)

 

5.2. Начально-краевая задача с неоднородной правой частью и неоднородными краевыми условиями. Постановка задачи включает УрЧП с неоднородной правой частью, разложимой в ряд Фурье

 

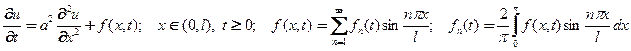(8)

 

начальное условие (неоднородное), разложимое в ряд Фурье

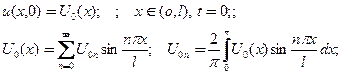(9)

 

Неоднородные краевые условия,

  Введениемновой искомой функции (11)

Однородные краевые условия,

Решение задается в форме ряда Фурье   (15)

Разложение по окружной координате

  приводит к системам уравнений : -при

Уравнение Лапласа. Постановка краевых задач для эллиптических УрЧП.

6.2.1.Уравнением Лапласаназывается однородное уравнение, содержащее дифференциальный оператор в области 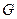, ограниченной контуром 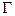, например, двумерный в декартовой системе координат

 

(1)

 

или в полярной системе координат

 

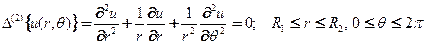(2)

 

Различают три типа краевых условий и соответственно три типа краевых задач.

6.2.2. Задача Дирихле (краевые условия первого рода): найти функцию, удовлетворяющую в заданной области уравнению Лапласа и принимающей на границе этой области заданное значение

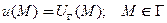(3)

6.2.3. Задача Неймана (краевые условия второго рода): найти функцию, удовлетворяющую в заданной области уравнению Лапласа и производная по нормали (поток) к ограничивающему эту область принимает на границе заданное значение

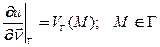(4)

 

6.2.4. Задача Робина (краевые условия третьего рода): найти функцию, удовлетворяющую в заданной области уравнению Лапласа и линейная комбинация производной по нормали к ограничивающему эту область и искомой функции принимает на границе заданное значение

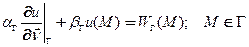(5)

Функции, удовлетворяющие уравнению Лапласа называют гармоническими.

6.3. Уравнение Пуассона. Если правая часть уравнения неоднородная (ненулевая) заданная (источники-стоки) функция УрЧП называется уравнением Пуассона:

- в декартовой системе координат

 

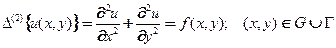(6)

 

или в полярной системе координат

 

(7)

 

Различают также три типа краевых условий и соответственно три типа краевых задач.

6.3.1. Задача Дирихле (краевые условия первого рода): найти функцию, удовлетворяющую в заданной области уравнению Пуассона и принимающей на границе этой области заданное значение

 

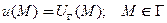(8)

6.3.2. Задача Неймана (краевые условия второго рода): найти функцию, удовлетворяющую в заданной области уравнению Пуассона и производная по нормали к ограничивающему эту область принимает на границе заданное значение

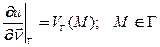(9)

 

Для однозначной разрешимости задачи Неймана для уравнения Пуассона из условия балансаграничныхпотокови внутреннихисточников-стоков

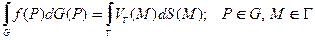(10)

6.3.3. Задача Робина (краевые условия третьего рода): найти функцию, удовлетворяющую в заданной области уравнению Пуассона и линейная комбинация производной по нормали к ограничивающему эту область и искомой функции принимает на границе заданное значение

 

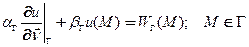(11)

 

Метод разделения переменных Фурье. Задачи для прямоугольника и кольца.

6.4.1. Задача Дирихле для прямоугольника с однородной правой частью и с однородными условиями на противоположных сторонах.

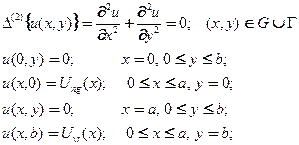(12)

 

Задача Дирихле (первого рода) для уравнения Лапласа сформулированная в таком виде позволяет принять решение в виде функции разделенных переменных

 

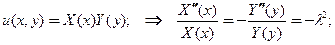(13)

 

откуда следует система ЛОДУ для первого набора собственных функций

 

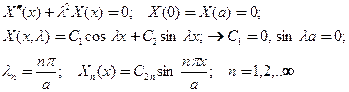(14)

 

и для второго набора

 

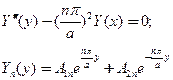(15)

 

где постоянные интегрирования в выражении «общего» решения

 

(16)

 

определяются изоставшихся краевых условий, представленных рядами Фурье по собственным функциям

 

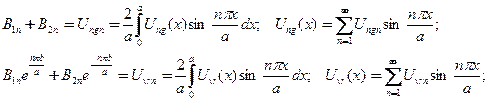
(17)

6.4.2. Задача Дирихле для прямоугольника с неоднородной правой частью, представимой разложением Фурье, и с однородными условиями на противоположных сторонах.

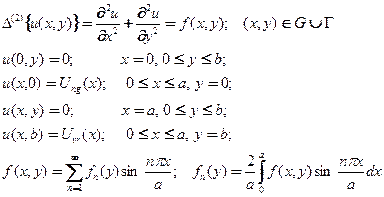(18)

 

Представляярешение задачи Дирихле для уравнения Пуассона в виде ряда Фурьепо собственным функциям

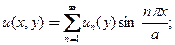(19)

 

для составляющих этого ряда имеем ЛОДУ второго порядка с постоянными коэффициентами

 

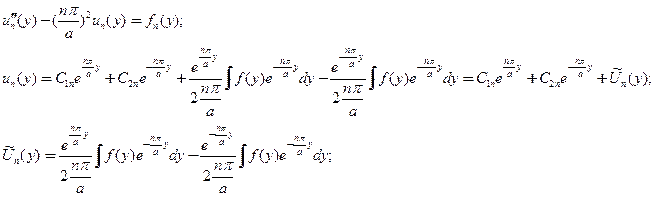
(20)

 

и «общее» решение представляется выражением

 

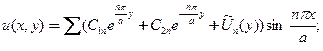(21)

 

где постоянные интегрирования определены системой алгебраических уравнений, составленным по оставшимся краевым условиям

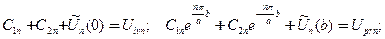(22)

6.4.3. Задача для прямоугольника с неоднородной правой частью и неоднородными условиями на противоположных сторонах

 

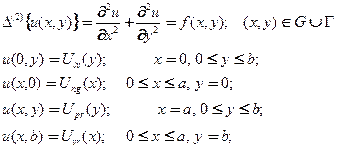(23)

 

где все заданные функции представимы соответствующими рядами Фурье

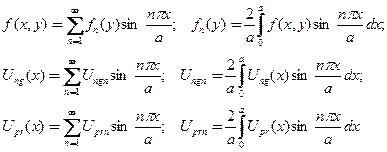(24)

Задача Дирихле (первого рода) для уравнения Пуассона в сформулированном в виде введением новой искомой функции выражением

 

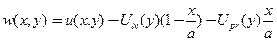(25)

 

сведена к предыдущей

 

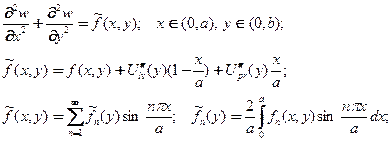(26)

 

с краевыми условиями

 

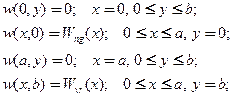(27)

 

здесь также заданные функции представимы соответствующими рядами Фурье

 

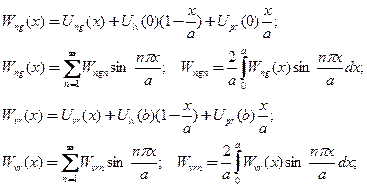(28)

 

Представляя новую искомую функцию рядом Фурье, компоненты которого есть решения неоднородного ЛОДУ второго порядка с постоянными коэффициентами

 

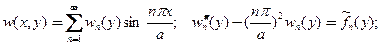
что дает

 

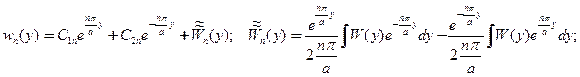(29)

 

И, окончательно, «общее» решение в виде ряда с неопределенными коэффициентами имеем в форме

 

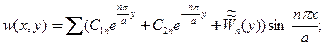(30)

 

где постоянные интегрирования определяются из оставшихся краевых условий

 

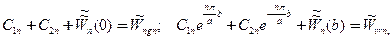(31)

 

И таким образом задача Дирихле для УрЧП Пуассона для прямоугольника при неоднородных краевых условиях дается в одинарных тригонометрических рядах Фурье.

 

ПРИМЕР.

Задание № 3-3.Методом разделения переменных (методом Фурье) решить задачу с уравнением в частных производных.

 

 

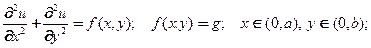
при заданных краевых условиях

 

 

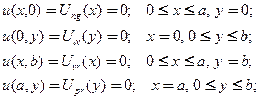
Разлагая правую часть уравнения в ряд Фурье

 

 

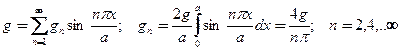
в результате имеем выражения для коэффициентов представления искомой функции

 

 

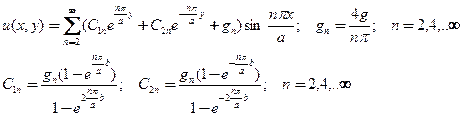
и содержит отличные от нуля только слагаемые с четными номерами, с нечетные -нулевые.

6.5. Общее решение УрЧП Пуассона для кругового кольца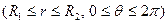

Записав оператор Лапласа в полярной системе координат

 

(32)

 

и правую часть,представимуюрядом Фурье, искомое решениетакже представляемрядом Фурье

 

 

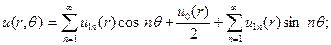(33)

 

компоненты которого определяются ЛОДУ второго порядка эйлерова типа

 

 

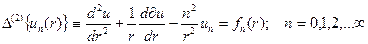(34)

 

Общее решение этой системы имеет вид

 

(35)

 

где постоянные интегрирования определяются из соответствующих краевых (граничных) условий.

 

Литература.

1. Арсенин В.Я. Математическая физика.Основные уравнения и специальные функции -М.: Наука, 1966 . -368 с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления.т.2 –М.: Наука. Физматлит, 1985. –554 с.

3.Тихонов А.Н., Самарский А.А.. Уравнения математической физики.–М.: Наука, 1966. – 724 с.

4.Смирнов В.И. Курс высшей математики. т.2. –М.: Наука, Физматлит. 1967. – 416 с.

5. Араманович И.Г., Левин В.И.. Уравнения математической физики. –М.: Наука, Физматгиз. 1969.- 287 с.

6. Михлин С.Г.. Уравнения математической физики. –М.: Наука, Физматгиз. 1968. – 575 с.

7. Петровский И.Г.. Лекции об уравнениях с частными производными. – М.: Физматлит. 1961.-400с.

8. Коган Е.А., Попович В.Е.. Ряды Фурье. Дифференциальные уравнения в частных производных. Теория вероятностей. Ч.2.(Методическое пособие № 1393 (1155)).-М.: МАМИ. 1988. –99с.

9. Коган Е.А., Лопаницын Е.А.. Ряды Фурье. Уравнения математической физики.

(Методическое пособие ).-М.: МАМИ. 2004. –89с.

10. Сборник задач по математике для втузов. Ч.1-2. /Болгов В.А., Ефимов А.В., Каракулин А.Ф., Коган С.М., Лунц Г.Л., Поспелов А.С., Фролов С.В., Шостак Р.Я., Янпольский А.Р..-М.: Наука, Физматгиз, 1986. –426 с.,– 368с.

11. Владимиров В.С.. Уравнения математической физики. –М.: Физматлит. 1967. – 436 с.

12. Соболев С.Л.. Уравнения математической физики. –М.: наука, Физматлит. 1966. -444 с.

13. Положий Г.Н.. Уравнения математической физики. – М.: Высшая школа. 1964. –560 с.

14. Годунов С.К.. Уравнения математической физики. –М.: Наука Физматлит. 1971. – 414 с.

15. Кошляков Н.С.. Основные уравнения математической физики. Фихматгиз. 1962. –892 с.

16. Будак Б.М., Самарский А.А., Тихонов А.Н.. Сборник задач по математической физике. –М.: Гостехиздат. 1956. –234 с.

17. Лебедев Н.Н., Скальский И.П., Уфлянд Я.С... Сборник задач по математической физике. –М.: Гостехиздат. 1955. –164 с.

18. Смирнов В.И.. Задачи по уравнениям математической физики. –М.: Наука. Физматиздат. 1956. –262 с.

 

 

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА по РАЗДЕЛУ УрЧП (УрМатФиз)

Задача № 1. Методом разделения переменных (методом Фурье-Эйлера) решить начально-краевую или краевую задачу с уравнениями в частных производных: тип решаемых задач и их формулировка приведены в таблице № 1.4. Исходные данные по каждому варианту решаемой задачи указаны в таблице № 1.5.

Таблица № 1.4.

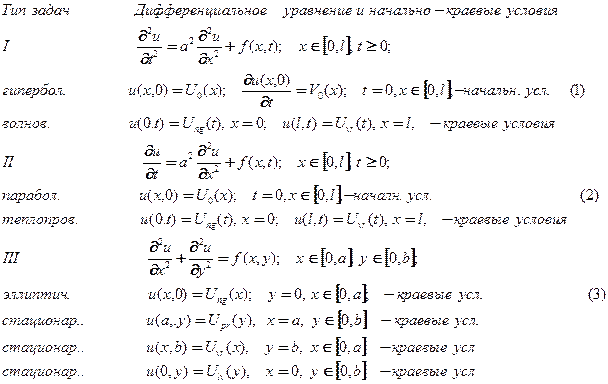
Таблица № 1.5.

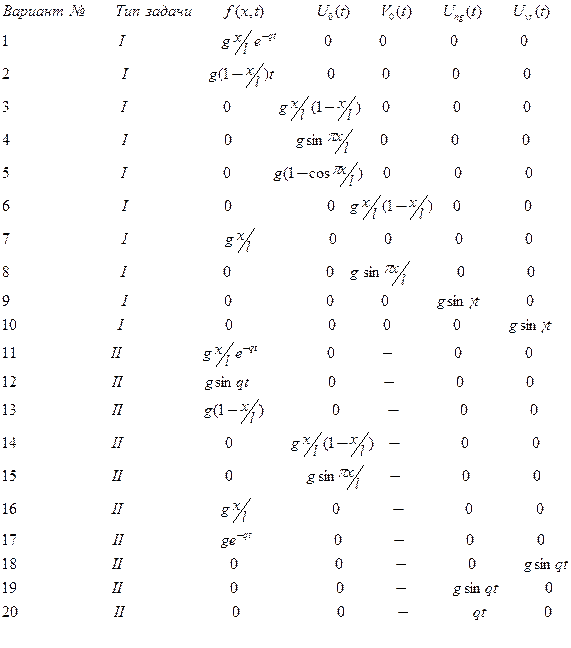
Таблица № 1.5. (продолжение)

 

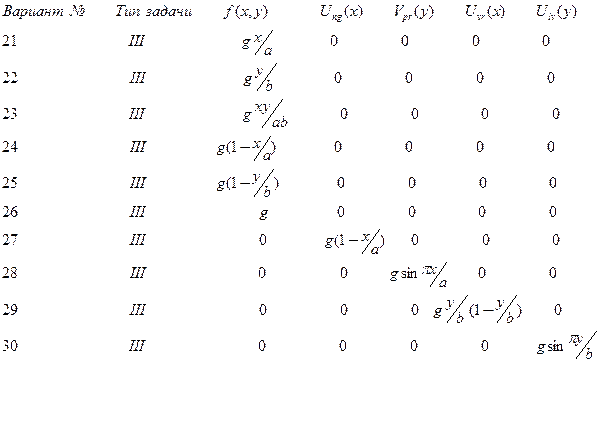
ВОПРОСЫ К ЗАЧЕТУ (гр. 4 АЭ 8-12) И К ЭКЗАМЕНУ (гр. 4 АЭ 13).

1. Понятия о функциональных ДУрЧП. Основные определения (порядок, линейность, область определения, однородность и неоднородность). 2. Каноническая форма УрЧП. Характеристики УрЧП (для гиперболических,… 3. Классификация УрЧП второго порядка: типы – классы гиперболические, эллиптические, параболические.