Выбрав удобную систему координат, мы можем написать

Т₁ = Т(х, у, z) и Т₂=Т(х + Dх, у + Dу, z + Dz),

где Dx:, Dy, Dz — компоненты вектора DR (фиг. 2.5). Вспомнив (2.7), напишем

 

 

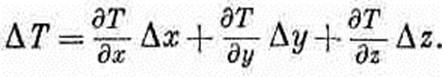
(2.13)

Слева в (2.13) стоит скаляр, а справа — сумма трех произведе­ний каких-то чисел на Dx;, Dy, Dz, которые являются компонен­тами вектора. Значит,

три числа — тоже х-, у- и z-компоненты вектора.

 

 

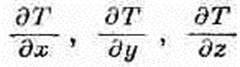
Фиг. 2.5. Вектор DR с компо­нентами Dх, Dу, Dz.

Мы напишем этот новый вектор при помощи символа ÑТ. Символ Ñ (называемый набла) — это D вверх ногами; он напоминает нам о дифференцировании. Читают Ñ T по-разному: «набла T», или «градиент T», или «gradT»:

 

 

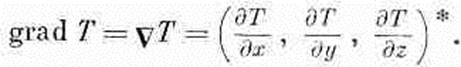
(2.14)

С этим обозначением (2.13) переписывается в более компакт­ной форме

 

 

(2.15)

Или, выражая словами: разница температур в двух близких точках есть скалярное произведение градиента Т на вектор смещения второй точки относительно первой. Форма (2.15) так­же служит иллюстрацией к нашему утверждению, что ΔТ — действительно вектор.

Быть может, вы еще не убеждены? Тогда докажем иначе. (Хотя, вглядевшись внимательно, вы увидите, что это на самом деле то же самое доказательство, только подлиннее!) Мы по­кажем, что компоненты ΔТ преобразуются абсолютно так же, как я компоненты R, а значит, ΔТ — тоже вектор в соответствии с первоначальным определением вектора в вып. 1, гл. 11. Мы выберем новую систему координат х', у', z' и в ней вычис­лим дТ/дх', дТ/ду'_: дТ/dz'. Для простоты положим z=z', так что о третьей координате мы можем позабыть. (Можете сами заняться проверкой более общего случая.)

 

 

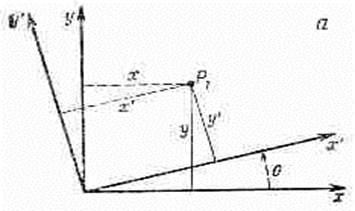
Фиг. 2.6. Переход к повернутой системе координат (а) и частный

случай интервала DR,параллель­ного к оси х (б).

Выберем систему х', у', повернутую относительно х, y-системы на угол 9 (фиг. 2.6, а). Координаты точки (х, у) в штрихованной системе имеют вид:

 

(2.16)

 

(2.17)

или, решая относительно x и y,

 

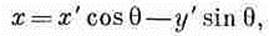
(2.18)

 

 

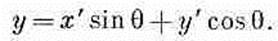
(2.19)

Если всякая пара чисел преобразуется так же, как x и y, то она является компонентами вектора.

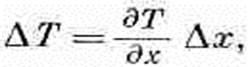
Рассмотрим теперь разницу в температурах двух сосед­них точек Р₁ и Р₂ (фиг. 2.6, б). В координатах х, у запишем

 

(2.20)

так как Dу = 0.

А в штрихованной системе? Там мы бы написали

 

(2.21)

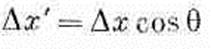
Глядя на фиг. 2.6, б, мы видим, что

 

(2.22)

и

 

(2.23)

так как Dy отрицательно при положительном Dx. Подстав­ляя в (2.21), получаем

 

(2.24)

 

 

(2.25)

Сравнивая (2.25) с (2.20), мы видим, что

 

(2.26)

Это уравнение говорит нам, что дТ/дх получается из дТ/дх' и дТ/ду' в точности так же, как х из х' и у' в (2.18). Значит, дТ/дх — это x-компонента вектора. Сходные же рассуждения показывают, что дТ/ду и dT/dz суть у- и z-компоненты. Стало быть, ÑТ есть на самом деле вектор. Это векторное поле, обра­зованное из скалярного поля Т.