Вторые производные векторных полей

Пока мы имели дело только с первыми производными. А почему не со вторыми? Из вторых производных можно соста­вить несколько комбинаций:

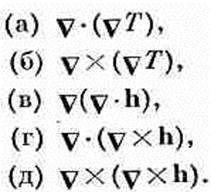
(2.45)

Вы можете убедиться, что никаких иных комбинаций быть не может.

 

Посмотрим сперва на вторую комбинацию (б). Она имеет ту же форму, что и

АX(АT) = (АXА)T = 0, потому что АXА всегда нуль. Значит,

 

(2.46)

Можно понять, как это получается, если расписать одну из компонент:

 

 

 

что равно нулю [по уравнению (2.8)]. Это же верно и для других компонент. Стало быть, ÑХ(ÑT)=0 для любого распределе­ния температур, да и для всякой скалярной функции.

Возьмем второй пример. Посмотрим, нельзя ли получить нуль другим путем. Скалярное произведение вектора на век­торное произведение, содержащее этот вектор, равно нулю

А•(АХВ) = 0, (2.48)

потому что АХВ перпендикулярно к А и не имеет тем самым составляющих вдоль А. Сходная комбинация стоит в списке (2.45) под номером (г):

Ñ(ÑXh) = div(roth) = 0. (2.49)

В справедливости этого равенства опять-таки легко убедиться, проделав выкладки на компонентах.

Теперь сформулируем без доказательства две теоремы. Они очень интересны и весьма полезны для физиков.

В физических задачах часто оказывается, что ротор какой-то величины (скажем, векторного поля А) равен нулю. Мы видели в уравнении (2.46), что ротор градиента равен нулю. (Это легко запоминается по свойствам векторов.) Далее, может оказаться, что А будет градиентом какой-то величины, потому что тогда ротор А с необходимостью обратится в нуль. Имеется интерес­ная теорема, утверждающая, что если ротор А есть нуль, то тогда А непременно окажется чьим-то градиентом; существует некоторое скалярное поле ψ; (пси), такое, что A=gradψ. Иными словами, справедлива

Т Е О Р Е М А

Если ÑXА = 0,

то имеется ψ, (2.50)

такое, что А = Ñψ.

. Сходная теорема формулируется и для случая, когда ди­вергенция А есть нуль. Из уравнения (2.49) видно, что дивер­генция ротора любой величины равна всегда нулю. Если вам случайно встретилось векторное поле D, для которого div D — нуль, то вы имеете право заключить, что D это ротор некоторого векторного поля С.

ТЕОРЕМА

Если Ñ•D = 0,

то имеется С, (2.51)

такое, что D = ÑXC.

Перебирая всевозможные сочетания двух операторов у, мы обнаружили, что два из них всегда дают нуль. Займемся теперь теми, которые не равны нулю. Возьмем комбинацию Ñ• (ÑT), первую в нашем списке. В общем случае это не нуль. Выпишем компоненты

 

 

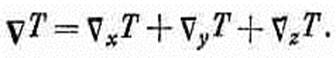
Далее,

 

 

(2.52)

что может, вообще говоря, быть любым числом. Это скаляр­ное поле.

Вы видите, что скобок можно не ставить, а вместо этого писать, не рискуя ошибиться:

 

(2.53)

Можно рассматривать Ѳ как новый оператор. Это скаляр­ный оператор. Так как он в физике встречается часто, ему дали особое имя — лапласиан.

 

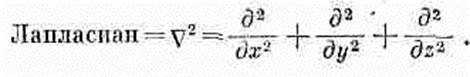
(2.54)

Раз оператор лапласиана —оператор скалярный, он может действовать и на вектор. Под этим мы подразумеваем, что он применяется к каждой компоненте вектора

 

Рассмотрим еще одну возможность: ÑX(ÑX h) [(д) в списке (2.45)]. Ротор от ротора можно написать иначе, если исполь­зовать векторное равенство (2.6)

АX(ВXС) = В(А•С)-С(А•В). (2.55)

Заменим в этой формуле А и В оператором у и положим C=h. Получится

ÑX(ÑXh) = Ñ(Ñb)-h(Ñ•Ñ)...???

Погодите-ка! Здесь что-то не так. Как и положено, первые два члена — векторы (операторы утолили свою жажду), но послед­ний член совсем не такой. Он все еще оператор. Ошибка в том, что мы не были осторожны и не выдержали нужного порядка членов. Вернувшись обратно, вы увидите, что (2.55) можно с равным успехом записать в виде

АX(ВXС) = В(А•С) -(А•В)С. (2.56)

Такой порядок членов выглядит уже лучше. Сделаем нашу под­становку в (2.56). Получится

ÑX (ÑXh) = Ñ (Ñh)-( Ñ•Ñ)h. (2.57)

С этой формулой уже все в порядке. Она действительно пра­вильна, в чем вы можете убедиться, расписав компоненты. По­следний член — это лапласиан, так что с равным успехом мож­но написать

ÑX (ÑXh) = Ñ(Ñ•h)- Ѳh. (2.58)

Из нашего списка (2.45) двойных Ñ мы разобрали все комби­нации, кроме (в), Ñ(Ñ•h). В ней есть смысл, это — векторное поле, но больше сказать о ней нечего. Это просто векторное поле, которое может случайно возникнуть в каком-нибудь рас­чете.

Удобно будет все наши рассуждения свести теперь в таблицу:

 

(2.59)

Вы могли заметить, что мы не пытались изобрести новый век­торный оператор ÑХÑ. Понимаете, почему?