Теплопроводность; уравнение диффузии

Чтобы привыкнуть к теореме, разберем на примере, как ее применяют. Обратимся опять к распространению тепла, скажем в металле, рассмотрим совсем простой случай: все тепло было подведено к телу заранее, а теперь тело остывает. Источников теп­ла нет, так что количество тепла сохраняется. Сколько же тогда тепла должно оказаться внутри некоего определенного объема в какой-то момент времени? Оно должно уменьшаться как раз на то количество, которое уходит с поверхности объема. Если этот объем — маленький кубик, то,
следуя формуле (3.17), мож­но написать

 

 

(3.19)

Но это должно быть равно скорости потери тепла внутренностью куба. Если q — количество тепла в единице объема, то весь

 

запас тепла в кубе qDV, а скорость потерь равна

 

(3.20)

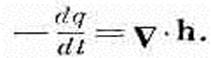
Сравнивая (3.19) с (3.20), мы видим, что

 

(3.21)

Внимательно вглядитесь в форму этого уравнения; эта форма часто встречается в физике. Она выражает закон сохра­нения, в данном случае закон сохранения тепла. В уравнении (3.13) тот же физический факт был выражен иначе. Там была интегральная форма уравнения сохранения, а здесь у нас — дифференциальная форма.

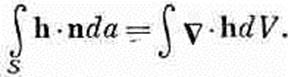
Уравнение (3.21) мы получили, применив формулу (3.13) к бесконечно малому кубу. Можно пойти и по другому пути. Для большого объема F, ограниченного поверхностью S, за­кон Гаусса утверждает, что

 

(3.22)

Интеграл в правой части можно, используя (3.21), преобразо­вать как раз к виду -dQ/dt, и тогда получится формула (3.13).

Теперь рассмотрим другой случай. Представим, что в блоке вещества имеется маленькая дырочка, а в ней идет химическая реакция, генерирующая тепло. Можно еще представить себе, что к маленькому сопротивлению внутри блока подведены про­волочки, нагревающие его электрическим током. Предположим, что тепло создается практически в одной точке, a W представ­ляет собой энергию, возникающую в этой точке за секунду. В остальной же части объема пусть тепло сохраняется и, кро­ме того, пусть генерация тепла началась так давно, что сейчас температура уже нигде больше не изменяется. Вопрос состоит в следующем: как выглядит вектор потока тепла h в разных точках металла? Сколько тепла перетекает через каждую точку?

Мы знаем, что если мы будем интегрировать нормальную составляющую h по замкнутой поверхности, окружающей источ­ник, то всегда получится W. Все тепло, которое генерируется в точечном источнике, должно протечь через поверхность, ибо предполагается, что поток постоянен. Перед нами трудная задача отыскания такого векторного поля, которое после ин­тегрирования по произвольной поверхности всегда давало бы W. Но мы сравнительно легко можем найти это поле, выбрав поверхность специального вида. Возьмем сферу радиусом R с центром в источнике и предположим, что поток тепла радиален (фиг. 3.6). Интуиция нам подсказывает, что h должен быть направлен по радиусу, если блок вещества велик и мы не приближаемся слишком близко к его границам; кроме того, вели­чина h во всех точках сферы должна быть одинакова.

 

Фиг. 3.6. В области близ точеч­ного источника поток тепла на­правлен по радиусу наружу.

Вы ви­дите, что для получения ответа к нашим выкладкам мы вы­нуждены добавить известное количество домыслов (обычно это именуют «физической интуицией»).

Когда h радиально и сферически симметрично, интеграл от нормальной компоненты h по площади поверхности вычис­ляется очень просто, потому что нормальная компонента в точ­ности равна h и постоянна. Площадь, по которой интегрируется, равна 4pR². Тогда мы получаем

 

(3.23)

где h — абсолютная величина h. Этот интеграл должен быть равен W — скорости, с которой источник генерирует тепло. Получается

 

 

 

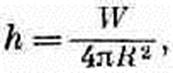
или

 

(3.24)

где, как всегда, e_r обозначает единичный вектор в радиаль­ном направлении. Этот результат говорит нам, что h пропорцио­нален W и меняется обратно квадрату расстояния от источника.

Только что полученный результат применим к потоку те­пла вблизи точечного источника тепла. Теперь попытаемся найти уравнения, которые справедливы для теплового потока самого общего вида (придерживаясь единственного условия, что количество тепла должно сохраняться). Нас будет интере­совать только то, что происходит в местах вне каких-либо ис­точников или поглотителей тепла.

Дифференциальное уравнение распространения тепла было получено в гл. 2. В соответствии с уравнением (2.44),

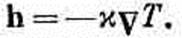
(3.25)

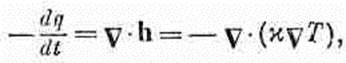
(Помните, что это соотношение приближенное, но для некоторых веществ вроде металлов выдерживается неплохо.) Применимо оно, конечно, только в тех частях тела, где нет ни выделения, ни поглощения тепла. Выше мы вывели другое соотношение (3.21), которое выполняется тогда, когда количество тепла сохраняется. Если мы это уравнение скомбинируем с (3.25), то получим

 

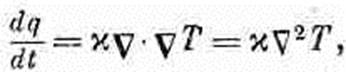
или

 

(3.26)

если c — величина постоянная. Напоминаю, что q — это количество тепла в единичном объеме, а Ñ•Ñ = Ѳ — лапласиан, т. е. оператор

 

 

 

Если мы теперь сделаем еще одно допущение, сразу воз­никнет одно очень интересное уравнение. Допустим, что тем­пература материала пропорциональна содержанию тепла в еди­нице объема, т. е. что у материала есть определенная удельная теплоемкость. Когда это допущение верно (а так бывает часто), мы можем писать

 

или

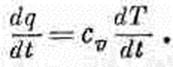
(3.27)

Скорость изменения количества тепла пропорциональна ско­рости изменения температуры. Коэффициент пропорциональ­ности c_v здесь — удельная теплоемкость на единицу объема материала. Подставляя (3.27) в (3.26), получаем

 

 

(3.28)

Мы обнаружили, что быстрота изменения со временем темпера­туры Т в каждой точке пропорциональна лапласиану от Т, т. е. вторым производным от пространственного распределения тем­ператур. Мы имеем дифференциальное уравнение — в перемен­ных х, у, z и t — для температуры Т.

Дифференциальное уравнение (3.28) называется уравнением диффузии тепла, или уравнением теплопроводности. Часто его пишут в виде

 

 

(3.29)

где D — постоянная. Она равна x/c_v.

 

Уравнение диффузии появляется во многих физических задачах: о диффузии газов, диффузии нейтронов и других. Мы уже обсуждали физику некоторых таких явлений в вып. 4, гл. 43. Теперь перед вами полное уравнение, описывающее диффузию в самом общем виде. Немного позже мы зай­мемся решением уравнения диффузии, чтобы посмотреть, как распределяется температура в некоторых случаях. А сейчас вернемся к рассмотрению других теорем о векторных полях.