Поток поля Е

Теперь мы хотим вывести уравнение, которое непосредственно и в лоб учитывает тот факт, что закон силы — это закон обратных квадратов. Кое-кому кажется «вполне естественным», что поле меняется обратно пропорционально квадрату расстояния, потому что «именно так, мол, все распространяется». Возьмите световой источник, из которого льется поток света; количество света, проходящее через основание конуса с вершиной в источнике, одно и то же независимо от того, насколько основание удалено от вершины. Это с необходимостью следует из сохранения световой энергии. Количество света на единицу площади — интенсивность — должно быть обратно пропорционально площади, вырезанной конусом, т. е. квадрату расстояния от источника. Ясно, что по той же причине и электрическое поле должно изменяться обратно квадрату расстояния!

Но здесь ведь нет ничего похожего на «ту же причину». Ведь никто не может сказать, что электрическое поле есть мера чего-то такого, что похоже на свет и что поэтому должно сохраняться. Если бы у нас была такая «модель» электрического поля, в которой вектор поля представлял бы направление и скорость (ну, например, был бы током) каких-то вылетающих маленьких «дробинок», и если бы эта модель требовала, чтобы число дробинок сохранялось и ни одна не могла пропасть после вылета из заряда, вот тогда мы могли бы говорить, что «чувствуем» неизбежность закона обратных квадратов. С другой стороны, непременно должен был бы существовать математический способ выражения этой физической идеи. Если бы электрическое поле было подобно сохраняющимся дробинкам, то оно менялось бы обратно пропорционально квадрату расстояния и мы могли бы описать такое поведение некоторым уравнением, т. е. чисто математическим путем. Если мы не утверждаем, что электрическое поле сделано из дробинок, а понимаем, что это просто модель, помогающая нам прийти к правильной математической теории, то ничего плохого в таком способе рассуждений нет.

Предположим, что мы на мгновение представили себе электрическое поле в виде потока чего-то сохраняющегося и текущего повсюду, за исключением того места, где расположен сам заряд (должен же этот поток откуда-то начинаться!).

Фиг. 4.5. Поток E из поверхности S равен нулю.

Представим что-то (что именно — неважно), вытекающее из заряда в окружающее пространство. Если бы Е было вектором такого потока (как h — вектор теплового потока), то вблизи от точечного источника оно обладало бы зависимостью 1/r². Теперь мы желаем использовать эту модель для того, чтобы глубже сформулировать закон обратных квадратов, а не просто говорить об «обратных квадратах». (Вам может показаться удивительным, почему вместо того, чтобы сходу, прямо и открыто сформулировать столь простой закон, мы хотим трусливо протащить то же самое, но с заднего хода. Немного терпения! Это окажется небесполезным.) Спросим себя: чему равно «вытекание» Е из произвольной замкнутой поверхности в окрестности точечного заряда? Для начала возьмем простенькую поверхность — такую, как показано на фиг. 4.5. Если поле Е похоже на поток, то суммарное вытекание из этого ящика должно быть равно нулю. Это и получается, если под «вытеканием» из этой поверхности мы понимаем поверхностный интеграл от нормальной составляющей Е, т. е. поток Е в том смысле, который был установлен в гл. 3. На боковых гранях нормальная составляющая Е равна нулю. На сферических гранях нормальная составляющая Е равна самой величине Е, с минусом на меньшей грани и с плюсом на большей. Величина Е убывает как 1/r², а площадь грани растет как r², так что их произведение от r не зависит. Приток Е через грань а в точности гасится оттоком через грань b. Суммарный поток через S равен нулю, а это все равно, что сказать, что

(4.30)

на этой поверхности.

Теперь покажем, что две «торцевые» поверхности могут быть без ущерба для величины интеграла (4.30) перекошены относительно радиуса. Хотя это верно всегда, но для наших целей

Фиг. 4.6. Поток Е из поверхности S равен нулю.

достаточно только показать, что это справедливо тогда, когда «торцы» малы и стягивают малый угол с вершиной в источнике, т. е. в действительности бесконечно малый угол. На фиг. 4.6 показана поверхность S, «боковые грани» которой радиальны, а «торцы» перекошены. На рисунке они не малы, но надо представить себе, что на самом деле они очень малы. Тогда поле Е над поверхностью будет достаточно однородным, так что можно взять его значение в центре. Если торец наклонен на угол q, то его площадь возрастает в 1/cosq раз, а Е_n — компонента Е, нормальная к поверхности торца, убывает в cosq раз, так что произведение Е_nDа не меняется. Поток из всей поверхности S по-прежнему равен нулю.

Теперь уже легко разглядеть, что и поток из объема, окруженного произвольной поверхностью S, обязан быть равным нулю. Ведь любой объем можно представить себе составленным из таких частей, как на фиг. 4.6. Вся поверхность разделится на пары торцевых участков, а поскольку потоки через каждую из них внутрь и наружу объема попарно уничтожаются, то и суммарный поток через поверхность обратится в нуль. Идея эта иллюстрируется фиг. 4.7. Мы получаем совершенно общий результат: суммарный поток Е через любую поверхность S в поле точечного заряда равен нулю.

Фиг. 4.7. Всякий объем можно представлять себе состоящим из бесконечно малых усеченных конусов.

Поток E сквозь один конец каждого конического сегмента равен и противоположен потоку сквозь другой конец. Общий поток из поверхности S поэтому равен пулю.

Фиг. 4.8. Если заряд находится внутри поверхности, поток наружу не равен нулю.

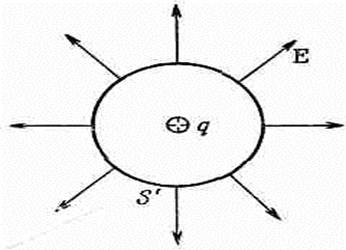
Будьте, однако, внимательны! Наше доказательство работает только тогда, когда поверхность S не окружает заряд. А что случилось бы, если бы точечный заряд оказался внутри поверхности? Как и раньше, поверхность можно было бы разделить на пары площадок, связанные радиальными прямыми, проходящими через заряд (фиг. 4.8). Потоки через эти участки по той же причине, что и раньте, по-прежнему попарно равны, но только теперь их знаки одинаковы. Поток из поверхности, окружающей заряд, не равен нулю. Тогда чему же он равен? Это можно определить с помощью фокуса. Допустим, что мы «убрали» заряд «изнутри», окружив его маленькой поверхностью S' так, чтобы она лежала целиком внутри первоначальной поверхности 5 (фиг. 4.9). Теперь в объеме, заключенном между двумя поверхностями S и S', никакого заряда нет. Общий поток из этого объема (включая поток через S') равен нулю, в чем можно убедиться при помощи прежних аргументов. Они говорят нам, что поток через S' внутрь объема такой же, как поток через S наружу.

Для S' мы можем выбрать любую, какую угодно форму, поэтому давайте сделаем ее сферой с зарядом в центре (фиг. 4.10). Тогда поток через нее подсчитать легко. Если радиус малой сферы равен r, то значение Е повсюду на ее поверхности равно

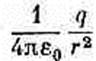
и направлено всегда по нормали к поверхности. Весь поток

Фиг. 4.9. Поток через S равен потоку через S'.

Фиг. 4.10.Поток через сферическую поверхность, охватывающую точечный заряд q, равен qle₀.

через S' получится, если эту нормальную составляющую Е умножить на площадь поверхности:

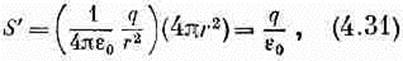
Поток через поверхность

т. е. равен числу, не зависящему от радиуса сферы! Значит, и поток наружу через S тоже равен q/e₀; это значение не зависит от формы S до тех пор, пока заряд q находится внутри. Наши выводы мы можем записать так:

(4.32)

Давайте вернемся к нашей аналогии с «дробинками» и посмотрим, есть ли в ней смысл. Наша теорема утверждает, что суммарный поток дробинок через поверхность равен нулю, если поверхность не окружает собой ружье, стреляющее дробью. А если ружье окружено поверхностью, то какого бы размера или формы она ни была, количество проходящих через нее дробинок всегда одно и то же — оно дается скоростью, с которой дробинки вылетают из ружья. Все это выглядит вполне разумно для сохраняющихся дробинок. Но сообщает ли эта модель нам хоть что-то сверх того, что получается просто из уравнения (4.32)? Никому не удалось добиться того, чтобы «дробинки» произвели на свет что-нибудь сверх этого закона. Кроме него, они порождают только ошибки. Поэтому-то мы сегодня предпочитаем чисто абстрактное представление об электромагнитном поле.