Поле заряженной прямой линии

Закон Гаусса может быть применен для решения множества задач, связанных с электрическим полем, обладающим специаль­ной симметрией (чаще всего сферической, цилиндрической или плоской). В оставшейся части этой главы мы займемся приме­нением закона Гаусса к некоторым задачам подобного рода. Легкость, с которой будут решаться эти задачи, может создать ошибочное впечатление о мощи метода и о возможности с его помощью перейти к решению многих других задач. К сожале­нию, это не так. Список задач, легко решаемых по закону Гаус­са, быстро исчерпывается. В дальнейших главах мы разовьем куда более мощные методы исследования электростатических полей.

В качестве первого примера рассмотрим систему с цилинд­рической симметрией. Пусть у нас имеется длинная-длинная равномерно заряженная спица. Под этим мы понимаем элект­рические заряды, равномерно распределенные по длине беско­нечно длинной прямой, так что на единицу длины приходится заряд l,. Мы хотим определить электрическое поле. Конечно, задачу можно решить интегрированием вкладов в поле от всех частей прямой. Но мы собираемся решить ее без интегрирова­ния, только с помощью закона Гаусса и некоторых догадок. Во-первых, легко догадаться, что электрическое поле будет направлено по радиусу. Любой осевой составляющей от зарядов, лежащих с одной стороны от некоторой плоскости, должна отве­чать такая же осевая составляющая от зарядов, лежащих с дру­гой стороны. В итоге должно остаться только радиальное поле. Кроме того, резонно полагать, что во всех точках, равноот­стоящих от прямой, поле имеет одинаковую величину. Это очевидно.

 

 

 

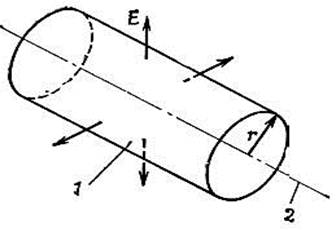
Фиг. 5.5. Цилиндрическая гауссо­ва поверхность, коаксиальная за­ряженной прямой.

1 — гауссова поверхность; 2 — заря­женная прямая.

 

(Может быть, это нелегко доказать, но это верно, если пространство симметрично, а мы считаем, что это так.) Применить закон Гаусса можно следующим образом. Вооб­разим себе поверхность, имеющую форму цилиндра, ось ко­торого совпадает с нашей прямой (фиг. 5.5). Согласно закону Гаусса, весь поток Е из этой поверхности равен заряду внутри нее, деленному на e₀. Раз поле считается нормальным к поверх­ности, то его нормальная составляющая — это величина векто­ра поля. Обозначим ее Е. Пусть радиус цилиндра будет r, а длина его для удобства выбрана равной единице. Поток сквозь цилиндрическую поверхность равен произведению Е на площадь поверхности, т. е. на 2pr. Поток через торцы равен нулю, потому что поле касательно к ним. Весь заряд внутри нашей поверх­ности равен как раз l, потому что длина оси цилиндра равна единице. Тогда закон Гаусса дает

 

 

(5.2)

Электрическое поле заряженной прямой обратно пропорцио­нально первой степени расстояния от прямой.