Это векторное уравнение, конечно, распадается на три урав­нения

 

 

и каждое из этих уравнений математически идентично уравнению

 

 

(14.17)

Все, что мы узнали о нахождении потенциала для извест­ного r, можно использовать для нахождения каждой компо­ненты А, когда известно j!

В гл. 4 мы видели, что общее решение уравнения элект­ростатики (14.17) имеет вид

 

 

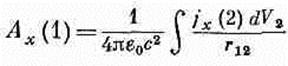
Тогда мы немедленно получаем общее решение для А_x:

 

 

(14.18)

и аналогично для А_у и A_z. (Фиг. 14.2 напоминает вам о при­нятых нами обозначениях для r₁₂ и dV₂.) Мы можем объ­единить все три решения в векторной форме:

 

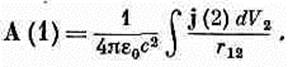
(14.19)

(Вы можете при желании проверить прямым дифференцирова­нием компонент, что этот интеграл удовлетворяет Ñ•А=0, поскольку Ñ•j=0, а последнее, как мы видели, должно вы­полняться для постоянных токов.)

Мы имеем, таким образом, общий метод вычисления маг­нитного поля от постоянных токов. Принцип такой: x-компонента векторного потенциала, возникающая от плотности тока j, точно такая же, как электрический потенциал j, который был бы создан плотностью зарядов р, равной j_x/c², и ана­логично для у- и z-компонент. (Этот принцип действует только для декартовых компонент. Например, «радиальная» компо­нента А не связана таким же образом с «радиальной» компонен­той j.) Итак, из вектора плотности тока j можно найти А, пользуясь уравнениями (14.19), т. е. мы находим каждую ком­поненту А, решая три воображаемые электростатические зада­чи для распределений заряда r₁=j_x/с², r₂=j_у/с² и r₃=j_z/с². Затем мы находим В, вычислив разные производные от А, входящие в ухА. Немного сложнее, чем в электростатике, но идея та же. Сейчас мы проиллюстрируем теорию, вычислив векторный потенциал в нескольких частных случаях.