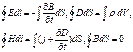Ток смещения. Уравнения Максвелла в интегральной форме.

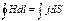Со­гласно теореме о цирку­ляции вектора Н : (1)

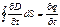
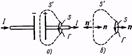Применим эту тео­рему к случаю, когда предварительно заря­женный плоский конденсатор разряжается через некото­рое внешнее сопротивление. В качестве кон­тура Г возьмем кривую, охватывающую провод. На кон­тур Г можно натянуть разные поверхности, например S и S'. Через поверхность S течет ток I, а через поверхность S' – нет. Получается, что циркуляция вектора Н зависит оттого, какую поверхность мы натягиваем на данный контур, чего явно не может быть. Поверхность S' «пронизывает» только электрическое поле. По теореме Гаусса поток вектора D сквозь замкнутую поверхность ∫DdS=q, откуда:

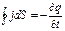С другой стороны, согласно уравнению непрерывности:

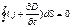Сложив отдельно левые и правые части уравнений, получим (4):

Это уравнение аналогично уравнению непрерывности для постоянного тока. Из него видно, что кроме плотности тока проводимости j имеется еще одно слагаемое дD/дt, раз­мерность которого равна размерности плотности тока. Это – плотность тока смещения: j_см = дD/дt. Сумму же тока проводимости и тока смещения называют полным током. Его плотность j_полн=j+дD/дt. Линии полного тока являются непрерывными в отличие от линий тока проводимости. Токи проводимости, если они не замкнуты, замыкаются токами смещения. Введение полного тока устраняет трудность, связанную с зависимостью циркуляции вектора Н от выбора поверхности, натягиваемой на контур Г. Для этого достаточно в правой части (1) вместо тока проводимости ввести полный ток, т. е. величину I_полн=∫(j+ дD/дt)dS. В самом деле, правая часть этого ур–ия представляет собой сумму тока проводимости I и тока смещения I_см: I_полн=I+I_см. Покажем, что полный ток I_полн будет одинаков и для поверхности S, и для поверхности S', натянутых на один и тот же контур Г. Для этого применим (4) к замк­нутой поверхности, составленной из поверхностей S и S'. Учитывая, что для замкнутой поверхности нормаль n направлена наружу:

I_полн(S')+I_полн(S)=0. Теперь, если обернуть нормаль n' для поверхности S' в ту же сторону, что и для S, то первое слагаемое в послед­нем уравнении изменит знак, и получим:

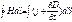I_полн(S') =I_полн(S), что и требовалось доказать.

Итак, теорему о циркуляции вектора Н можно обобщить для произвольного случая:

В таком виде теорема о циркуляции вектора Н справедлива всегда.

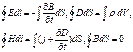Уравнения Максвелла в интегральной форме.Открытие тока смещения (дD/дt) позволило Максвеллу создать еди­ную теорию электрических и магнитных явлений. Её можно представить в виде си­стемы фундаментальных уравнений электродинамики, называемых уравнениями Максвелла в непод­вижных средах. В интегральной форме:

где ρ — объемная плотность сторонних зарядов, j — плотность тока проводимости. Содер­жание этих уравнений заключается в следующем: 1. Циркуляция вектора Е по любому замкнутому кон­туру равна со знаком минус производной по времени от магнитного потока через любую поверхность, ограничен­ную данным контуром. При этом под Е понимается не толь­ко вихревое электрическое поле, но и электростатическое (циркуляция последнего равна нулю).2. Поток вектора D сквозь любую замкнутую поверх­ность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью.3. Циркуляция вектора Н по любому замкнутому кон­туру равна полному току (току проводимости и току сме­щения) через произвольную поверхность, ограниченную данным контуром.4. Поток вектора В сквозь произвольную замкнутую поверхность всегда равен нулю. Из уравнений Максвелла следует, что электрическое и магнитное поля нельзя рассматривать как независимые.