ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ И ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ
Для того чтобы получить аналитическое выражение прогибов и углов поворота, необходимо найти решение дифференциального уравнения (9.5).
Правая часть уравнения (9.5) является известной функцией от z, поэтому имеем простое дифференциальное уравнение. Интегрируя его первый раз, получим
(а)
Это выражение определяет закон изменения углов поворота касательной по длине балки.
После повторного интегрирования находим уравнение оси изогнутого бруса:
(б)
Для вычисления интегралов, входящих в выражения (а) и (б), необходимо сначала написать аналитические выражения изгибающего момента и жесткости. Постоянные интегрирования С и D находятся из граничных условий, которые зависят от способов закрепления бруса.
Для уяснения сказанного рассмотрим примеры.
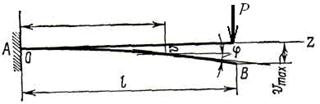1. Составить выражение прогиба и угла поворота в произвольном сечении консольной балки, загруженной силой Р (рис. 227). Рассматривая равновесие правой отсеченной части, найдем
М = – P (l - z).
Знак минус взят потому, что нижние волокна Рис. 227 балки сжаты. Так как ось Оу направлена кверху, то в правой части дифференциального уравнения (9.5) надо взять знак плюс:
Для нашего случая имеем
Предположим, что жесткость балки постоянна. Интегрируя один раз, получим
(в)
Интегрируя еще раз, имеем
(г)
Так как в заделке прогиб и угол поворота равны нулю, то для определения постоянных будем иметь следующие граничные условия:
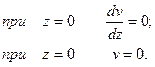
Из уравнения (в) видно, что постоянная С представляет собой угол поворота в начале координат. Положив z = 0, находим С = 0. Из уравнения (г) следует, что постоянная D – это прогиб в начале координат. Положив в уравнении (г) z = 0, получаем D = 0.
Итак, имеем:
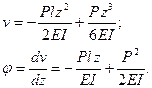
Из рис. 227 видно, что наибольший прогиб будет под грузом. Положив z=l, из первого уравнения найдем
Угол поворота на конце балки
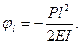
Знак минус у прогиба свидетельствует о том, что его направление не совпадает с положительным направлением оси у, минус в выражении угла поворота показывает, что касательная не проходит в положительной четверти осей координат.
2. Определим прогибы двухопорной балки постоянного сечения, показанной на рис. 228.
Так как ось у направлена вниз, то в дифференциальном уравнении необходимо взять знак минус:
Рис. 228
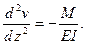
Изгибающий момент в произвольном сечении равен
Таким образом, дифференциальное уравнение запишется в следующем виде:
Последовательное интегрирование дает:
(д)
(е)
Для определения двух постоянных С и D необходимо иметь два условия. В рассматриваемом случае на левом и на правом концах прогиб равен нулю. Таким образом, граничные условия равны: при z = 0 v = 0; при z = l v = 0.
Подставляя в уравнение (е) z = 0 и приравнивая прогиб нулю, получим D=0; подставляя в это же уравнение z = l и также приравняв прогиб нулю, имеем
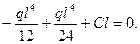
Следовательно,
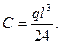
Найденные значения постоянных подставим в уравнения (д) и (е) и получим уравнения прогибов и углов поворота:
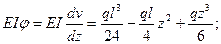
Давая теперь абсциссе z определенные значения, получим численные величины прогибов и углов поворота в определенных сечениях палки. Таким образом, можно вычислить прогиб и поворот сечения в середине пролета, в четверти пролета и т. п.
Если в точке, где прогиб наибольший, функция прогибов имеет максимум, то для нахождения этой точки необходимо приравнять нулю первую производную от v, т. е. выражение для угла поворота. В данной задаче наибольший прогиб определяют из условия симметрии. Он находится посередине пролета. Положив z = l/2, получим
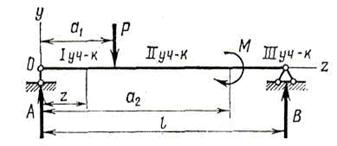Если на различных участках балки момент (или жесткость) имеет разные законы изменения, то необходимо составить несколько дифференциальных уравнений, каждое из которых отвечает своему участку. В соответствии с этим число произвольных постоянных равно удвоенному числу Рис. 229 участков интегрирования. Для определения постоянных всегда можно установить условия на границах каждого участка (граничные условия). Так, например, из условий непрерывности и гладкости оси изогнутого бруса вытекает, что на левом конце какого-либо участка прогиб и угол поворота будут такими же, как на правом конце предшествующего участка.
Граничные условия приведут к системе уравнений, число которых соответствует числу постоянных. Совместное решение уравнений позволит найти постоянные и получить для каждого участка уравнение прогибов и углов поворота. Однако необходимость решения совместных уравнений очень сильно усложняет задачу, поэтому непосредственное интегрирование применяют только в тех случаях, когда число участков невелико (один – два).
Рассмотрим балку, показанную на рис. 229. В данном случае имеем три участка, для которых изгибающие моменты равны:
Дифференциальные уравнения имеют вид:
для первого участка
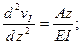
для второго участка
для третьего участка
Интегралы этих уравнений:
для первого участка
для второго участка
для третьего участка
Для определения шести произвольных постоянных имеется шесть граничных условии: при z = 0 v1(0) = 0; при z = a1 прогибы и углы поворота для двух прилегающих участков одинаковы:
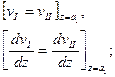
при z = а2 также имеют место равенства
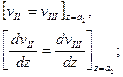
при z=l
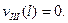
Выполняя эти условия, получив шесть уравнений с шестью неизвестными, которые необходимо совместно решить. Задача сильно усложняется, поэтому не будем доводить ее до конца.
В данном случае преследовалась цель показать методику и выяснить трудности, возникающие при решении задач, в которых балка загружена произвольной нагрузкой.
Для решения таких задач применяют другие методы, которые излагаются ниже.