ДИАГРАММА ПРЕДЕЛЬНЫХ АМПЛИТУД

Экспериментально установлено, что предел выносливости при асимметричном цикле больше, чем при симметричном, и зависит от степени асимметрии цикла:

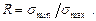
При графическом изображении зависимости предела выносливости от коэффициента асимметрии необходимо для каждого R определить свое значение предела выносливости. Сделать это затруднительно, так как в диапазоне от симметричного цикла до простого растяжения укладывается бесконечное количество самых разнообразных циклов. Опытное определение для каждого вида цикла из-за большого количества образцов и длительного времени их испытания почти невозможно.

Вследствие указанных причин по ограниченному числу опытов для трех-четырех значений R строят диаграмму предельных циклов.

Рис. 445

Предельным циклом называют такой, у которого максимальное напряжение равно пределу выносливости, т. е. . По оси ординат диаграммы откладываем значение амплитудного , а по оси абсцисс – среднего 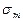напряжений предельного цикла. Каждая пара напряжений и 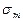, определяющая предельный цикл, изображается некоторой точкой на диаграмме (рис. 445). Как показал опыт, эти точки в общем случае располагаются на кривой АВ, которая на оси ординат отсекает отрезок, равный пределу выносливости симметричного цикла 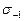(при этом цикле 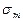= 0), а на оси абсцисс – отрезок, равный пределу прочности. В этом случае действуют постоянные во времени напряжения:

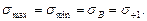(19.6)

Таким образом, диаграмма предельных циклов характеризует зависимость между величинами средних напряжений и величинами предельных амплитуд цикла.

Любая точка М, расположенная внутри этой диаграммы, соответствует некоторому циклу, определяемому величинами 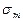(СМ) и (ME).

Для определения 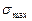, цикла из точки М проводят отрезки MN и MD до пересечения с осью абсцисс под углом 45° к ней. Тогда (рис. 445):

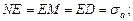
Циклы, у которых коэффициенты асимметрии одинаковы (подобные циклы), будут характеризоваться точками, расположенными на прямой 01, угол наклона которой определяется формулой

Рис. 446

Точка 1 соответствует предельному циклу из всех указанных подобных циклов. С помощью диаграммы можно определить предельные напряжения для любого цикла, например для пульсирующего (отнулевого) 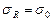, у которого 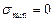, а 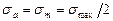(рис. 446). Для этого из начала координат (рис. 445) проводят прямую под углом α₁ = 45° () до пересечения с кривой в точке 2. Координаты этой точки: ордината Н2 равна предельному амплитудному напряжению, а абсцисса К2 – предельному среднему напряжению этого цикла. Предельное максимальное напряжение пульсирующего цикла равно сумме координат точки 2:

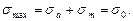(19.7)

Подобным образом можно решить вопрос о предельных напряжениях любого цикла.

Если деталь машины, испытывающая переменные напряжения, изготовлена из пластичного материала, то опасным будет не только усталостное разрушение, но и возникновение пластических деформаций. Максимальные напряжения цикла в этом случае определяются равенством

(19.8)

где 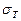– предал текучести.

Точки, удовлетворяющие этому условию, располагаются на прямой DC, наклоненной под углом 45° к оси абсцисс (рис. 447, а), так как сумма координат любой точки этой прямой равна .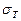

Если прямая 01 (рис. 447, а), соответствующая данному виду цикла, при увеличении нагрузок на деталь машины пересекает кривую АС, то произойдет усталостное разрушение детали. Если же прямая 01 пересекает линию CD, то деталь выйдет из строя в результате появления пластических деформаций.

Часто на практике пользуются схематизированными диаграммами предельных амплитуд. Кривую ACD (рис. 447, а) для пластических материалов приближенно заменяют прямой AD. Эта прямая отсекает на осях координат отрезк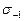и и 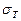. Уравнение имеет вид

Рис. 447

(19.9)

Для хрупких материалов диаграмму ограничивают прямой А В с уравнением

(19.10)

Наибольшее распространение получили диаграммы предельных амплитуд, построенные по результатам трех серий испытаний образцов: при симметричном цикле 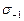(точка А), при отнулевом цикле (точка С) и статическом разрыве 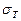(точка D) (рис. 447, б). Соединяя точки А и С прямой и проводя из D прямую под углом 45°, получим приближенную диаграмму предельных амплитуд. Зная координаты точки А [0, 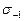] и С [0,5; 0,5], можно составить уравнение прямой АВ. Возьмем на прямой произвольную точку К с координатами и . Из подобия треугольников АСА₁ и КСК₁ получим

откуда находим уравнение прямой АВ в виде

(19.11)

где

.