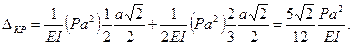МЕТОД НАЧАЛЬНЫХ ПАРАМЕТРОВ
 Задача определения прогибов может быть значительно упрощена, если применять так называемое универсальное уравнение оси изогнутого бруса, или, как часто говорят, универсальное уравнение упругой линии. Вывод универсального уравнения основан на так называемом методе начальных, параметров, который широко применяют в строительной механике. По этому методу прогиб в любом сечении балки определяется через перемещения и силовые факторы, взятые и начале координат с учетом приложенной к балке нагрузки.
Задача определения прогибов может быть значительно упрощена, если применять так называемое универсальное уравнение оси изогнутого бруса, или, как часто говорят, универсальное уравнение упругой линии. Вывод универсального уравнения основан на так называемом методе начальных, параметров, который широко применяют в строительной механике. По этому методу прогиб в любом сечении балки определяется через перемещения и силовые факторы, взятые и начале координат с учетом приложенной к балке нагрузки.
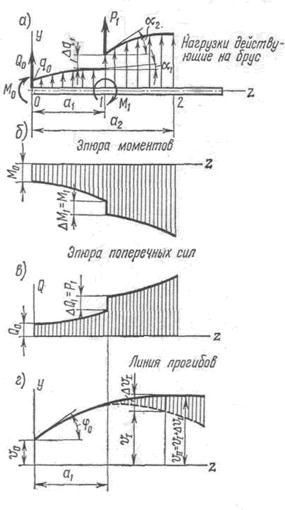
Представим себе, что на брус действует произвольная система нагрузок, показанная на рис.230, а.
| Рис. 230 |
Интенсивность нагрузки и сосредоточенные силы считают положительными, если их направление совпадает с направлением оси Оу, которую направим вверх. Внешние сосредоточенные моменты будут положительны, если они действуют по ходу часовой стрелки. Начало координат совместим с центром тяжести сечения на левом конце балки. Жесткость балки считают постоянной по всей ее длине.
Разобьем балку на ряд участков таким образом, чтобы на протяжении каждого участка изгибающий момент выражался с помощью непрерывной функции:
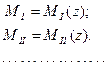
(Для упрощения записи в дальнейшем индексы х у моментов и у у поперечных сил ставить не будем.) Граничные точки 1, 2, ..., разделяющие участки, должны быть поставлены в тех сечениях, в которых происходят какие-либо изменения в законе распределения нагрузки Так, например, имеется скачок в нагрузке Δq или изменяется закон ее распределения, приложен сосредоточенный момент, создающий скачок в эпюре моментов: ΔM = Mi или сосредоточенная сила Р, создающая скачок в эпюре Q (ΔQ = Pi),
Рассмотрим сначала первый участок, прилегающий к началу координат, для которого согласно (9.5) дифференциальное уравнение имеет вид
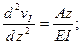 (a)
(a)
Здесь vI – прогиб в произвольном сечении первого участка;
МI – функция, выражающая значение изгибающего момента в
произвольном сечении первого участка
Разложим функцию прогиба vI в ряд Маклорена:
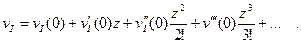 (б)
(б)
В этом уравнении величины vI (0); v’I (0); v’’I (0) ит. п. представляют собой значения функции vI (z) иее производных, взятые в начале координат, т.е. при z = 0.
Запишем дифференциальные зависимости
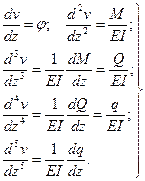 (в)
(в)
При дальнейшем дифференцировании имеем
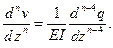
Положим z = 0 и обозначим:
vI (0) = v0 и v’I (0) = φ0 – прогиб и угол поворота в начале координат;
MI (0) = М0 и QI (0) = Q0 – момент и поперечная сила в сечении, взятом в
начале координат;
q0 , q0’ , q0’’, q0’’’ – интенсивность нагрузки и ее производные,
взятые в начале координат, т. е. при z = 0.
Тогда на основании дифференциальных зависимостей (в) между коэффициентами ряда Маклорена (б) и принятыми обозначениями имеем следующие равенства:
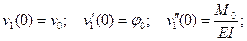
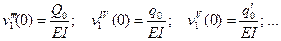 и т. п.
и т. п.
Подставляя эти значения в уравнение (б), получим
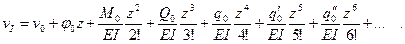 (9.6)
(9.6)
Полученное уравнение позволяет выразить прогибы в любом сечении первого участка через начальные параметры v0, ф0, Мо, Qo ... и т. д. Часть из этих параметров известна заранее, а часть подлежит определению из граничных условий.
Для того чтобы получить уравнение прогибов оси балки на втором участке, поступим следующим образом.
По уравнению (9.6), полученному для первого участка, построим линию прогибов в пределах двух участков – первого и второго. На протяжении первого участка (рис. 230, г) она изображена жирной линией, на протяжении второго участка – пунктиром. Пунктирная линия представляет собой изображение линии, описанной уравнением (9.6), но она не совпадает с истинной кривой оси изогнутого бруса для второго участка, которая проведена жирной линией. Ординаты между двумя указанными кривыми заштрихованы на чертеже. Аналитически эти ординаты выражаются равенством
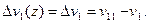 (г)
(г)
Определим величину ΔvI, а затем найдем ординаты прогибов балки на втором участке:
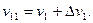 (д)
(д)
Для этой цели напишем два дифференциальных уравнения:
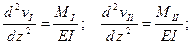
Вычитая первое уравнение из второго, получим
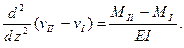
Обозначив
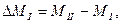
имеем
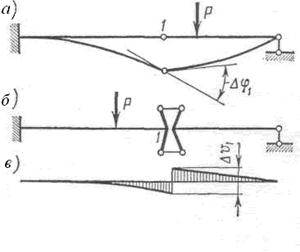
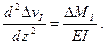 (е)
(е)
На основании сходства дифференциального уравнения (е) с основным уравнением (а) можно утверждать, что решение для функции ΔvI совпадает с решением, полученным для функции (9.6).
В этом решении вместо координаты z придется теперь брать координату, отсчитанную от точки 1, т. е. (z – а1). Вместо величин М0, Q0, q0,…, и т. д. придется брать ΔM1, ΔQ1, Δq1,….
Следовательно,
| Рис. 231 |
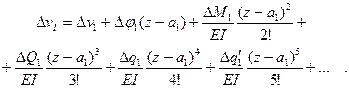 (9.7)
(9.7)
Здесь 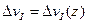 – функция, определяемая равенством (г) для второго
– функция, определяемая равенством (г) для второго
участка (рис. 230, г);
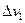 – скачок в линии прогибов в точке 1 (на рис. 230, г не
– скачок в линии прогибов в точке 1 (на рис. 230, г не
показан);
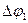 – скачок в угле поворота в точке 1 (на рис. 230, г не
– скачок в угле поворота в точке 1 (на рис. 230, г не
показан);
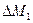 – скачок в эпюре моментов в точке 1 (рис. 230, б).
– скачок в эпюре моментов в точке 1 (рис. 230, б).
Эта величина равна внешнему сосредоточенному
моменту, приложенному в данной точке;
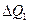 – скачок в эпюре поперечных сил (рис. 230, в),
– скачок в эпюре поперечных сил (рис. 230, в),
равный внешней сосредоточенной силе,
приложенной в точке 1;
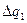 – скачок в интенсивности нагрузки в точке 1;
– скачок в интенсивности нагрузки в точке 1;
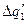 – скачок в производной от интенсивности нагрузки в
– скачок в производной от интенсивности нагрузки в
точке 1.
Все перечисленные здесь величины скачков определяются как разности двух значений соответствующих величин, взятых в точке 1.
Так, например,
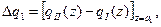 (9.8)
(9.8)
где 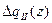 и
и 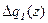 – функции, определяющие закон изменения распределенных нагрузок на втором и первом участках.
– функции, определяющие закон изменения распределенных нагрузок на втором и первом участках.
Величина 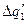 определяется как разность производных:
определяется как разность производных:
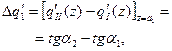 (9.9)
(9.9)
Здесь 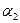 и
и 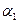 – углы наклона касательных к эпюре нагрузок, взятых в точке 1 (рис. 230, а).
– углы наклона касательных к эпюре нагрузок, взятых в точке 1 (рис. 230, а).
Скачок в угле поворота может иметь место в случае, если в точке 1 поставлен шарнир, из-за которого углы поворота слева и справа от  точки 1 будут различны (рис. 231, а). Скачок в прогибах возможен в том случае, если в точке 1 балка разрезана на две части, которые соединены параллельными стерженьками, как это показано на рис. 231, б. Вследствие этого прогибы двух балок в точке 1 будут отличаться друг от друга на
точки 1 будут различны (рис. 231, а). Скачок в прогибах возможен в том случае, если в точке 1 балка разрезана на две части, которые соединены параллельными стерженьками, как это показано на рис. 231, б. Вследствие этого прогибы двух балок в точке 1 будут отличаться друг от друга на 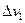 как это показано на эпюре прогибов (рис. 231, в).
как это показано на эпюре прогибов (рис. 231, в).
Для непрерывных балок, которые по всей длине, в том числе в точке 1, не имеют разрезов и полных шарниров, 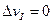 , и
, и 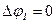 . Если теперь учесть, что
. Если теперь учесть, что
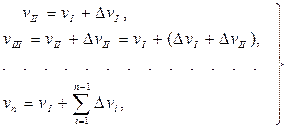 (ж)
(ж)
и вместе с тем воспользоваться уравнениями (9.6) и (9.7), то получим
| Рис. 232 |
универсальное уравнение прогибов для произвольного участка
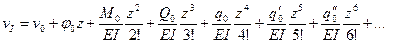
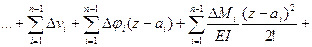
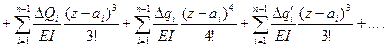 (9.10)
(9.10)
Путем дифференцирования получим универсальное уравнение для углов поворота
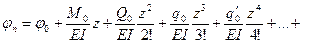
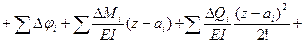
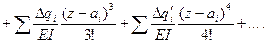 (9.11)
(9.11)
При решении каких-либо частных задач целый ряд членов, входящих в уравнения (9.10) и (9.11), равен нулю. Полученные уравнения, (9.10) и (9.11) зависят от величин 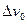 v0; ц>0; Мо; Qo; qn; q'a и т. п., которые берутся в начале координат, поэтому метод решения по указанным уравнениям носит название метода начальных параметров.
v0; ц>0; Мо; Qo; qn; q'a и т. п., которые берутся в начале координат, поэтому метод решения по указанным уравнениям носит название метода начальных параметров.
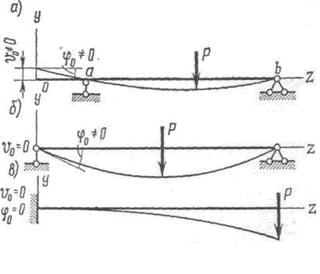
Из всех перечисленных начальных параметров некоторые параметры могут быть неизвестны. Величины q0 и q'0 по условию задачи обычно заданы. Мо и Qo могут быть известны или должны быть определены из условий статики, а в тех случаях, когда задача статически неопределима, – из условия деформаций. Величины v0 и φ0 не могут быть определены из условий статического равновесия. Определение этих начальных параметров производят по граничным условиям. Так, например, для балки, показанной на рис. 232, а, в начале координат v0 и φ0 не равны нулю. Они могут быть определены из условий равенства нулю прогибов на опорах а и b.
Основное преимущество метода начальных параметров состоит именно в том, что независимо от числа участков и нагрузки число постоянных, которые надо определить в статически определимой балке, не превышает двух.
Для балки, изображенной на рис. 232, б, начальный прогиб равен нулю, неизвестным остается начальный угол поворота φ0 . Для его определения надо использовать условие равенства нулю прогиба на правой опоре. Для случая, представленного на рис. 232, в, начальный прогиб и начальный угол поворота равны нулю.
После того как будут найдены начальные параметры, можно написать окончательные аналитические выражения прогибов и углов поворота для каждого участка балки. Придавая величине z ряд значений и вычисляя в соответствующих точках численные значения прогибов и углов поворота, можно построить линию прогибов и линию углов поворота оси балки.
В технических задачах часто ставится вопрос об определении места и величины наибольшего прогиба балки. Для определения местоположения сечения, в котором прогиб приобретает наибольшее значение, необходимо приравнять нулю производную:
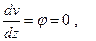 (9.12)
(9.12)
откуда можно определить абсциссу наибольшего прогиба.
В некоторых случаях наибольший прогиб не совпадает с экстремальным значением функции, так, в случае, показанном на рис. 232, в, в месте наибольшего прогиба условие (9.12) не выполняется. Тогда приходится исходить из общей картины возможных деформаций системы и определять место наибольшего прогиба путем анализа всей линии прогибов.
Рассмотрим ряд примеров применения универсального уравнения для определения перемещений в балке при изгибе.
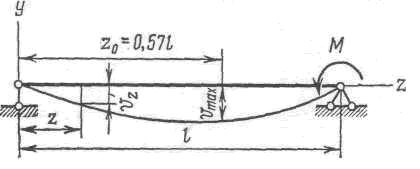
1. Составить уравнения прогибов и углов поворота, а также определить место положения и величину наибольшего прогиба в балке, изображенной на рис. 233. В данной балке всего один участок, так
| Рис. 233 |
как на всем протяжении балки нет никаких изменений в нагрузке. По универсальному уравнению (9.10) с учетом того, что 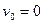 ,
, 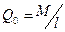 , имеем
, имеем
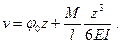
Для определения неизвестной величины угла поворота используем граничное условие: при 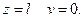
Таким образом,
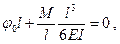
откуда находим
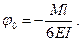
Следовательно, уравнение прогибов имеет вид
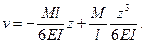 (з)
(з)
Дифференцируя, получим уравнение углов поворота
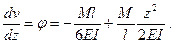
Для того чтобы определить расстояние до места наибольшего прогиба z0, воспользуемся условием
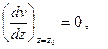
или
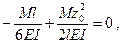
откуда
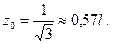
Подставляя найденное значение z0 в уравнение (з), получим
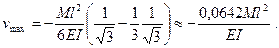
Интересно отметить, что этот прогиб очень мало отличается от прогиба в середине пролета:
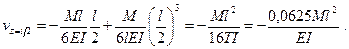
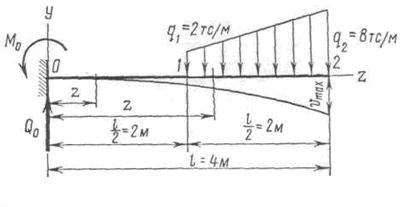
2. Написать уравнение прогибов и углов поворота для балки, показанной на рис. 234, и определить наибольший прогиб.
| Рис. 234 |
Поместив начало координат в заделку, имеем:
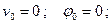
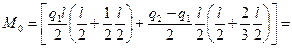
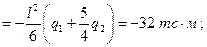
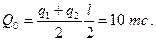
Для первого участка по формуле (9.10) получаем уравнение прогибов
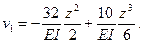
Это уравнение справедливо для случаев, когда 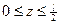 . К точке 1 примыкают два участка: на первом участке в точке 1 q = 0, на втором участке в этой же точке q= – q1 . При переходе через точку 1 от первого ко второму участку нагрузка изменяется от 0 до – q1 . Следовательно, Δq1 = – q1 . Для того, чтобы не сделать ошибки в определении величин и знаков Δq1 и Δq’1 , следует пользоваться формулами (9.8) и (9.9).
. К точке 1 примыкают два участка: на первом участке в точке 1 q = 0, на втором участке в этой же точке q= – q1 . При переходе через точку 1 от первого ко второму участку нагрузка изменяется от 0 до – q1 . Следовательно, Δq1 = – q1 . Для того, чтобы не сделать ошибки в определении величин и знаков Δq1 и Δq’1 , следует пользоваться формулами (9.8) и (9.9).
По этим формулам находим
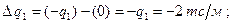
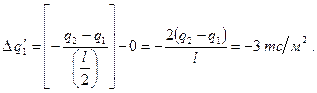
Скачки в моменте и поперечной силе отсутствуют ΔM1 = 0, ΔQ1 = 0.
Применяя формулу (9.10), получим уравнение для прогибов на втором участке
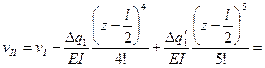
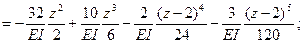
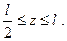
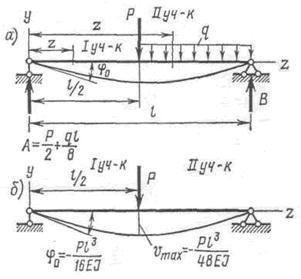 Уравнения углов поворота получим дифференцированием уравнений прогибов:
Уравнения углов поворота получим дифференцированием уравнений прогибов:
для первого участка
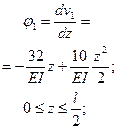
| Рис. 235 |
для второго участка
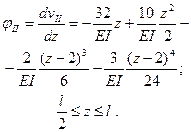
Наибольший прогиб vmax будет на правом конце балки; подставляя 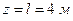 в уравнение прогибов для второго участка, получим
в уравнение прогибов для второго участка, получим
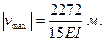
Так как в решении размеры балки принимались в метрах и нагрузка – в тоннах на погонный метр, то величины Е и J надо брать в тс/м2 и м4.
3. Написать уравнение прогибов балки, показанной на рис. 235, а, и определить прогиб посередине пролета.
Начальные параметры для данной задачи имеют следующие значения:
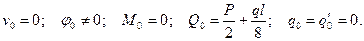
Для первого участка согласно универсальному уравнению прогиб определяют по формуле
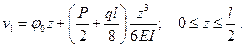
В точке перехода от участка I к участку II имеем
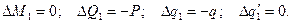
Следовательно,
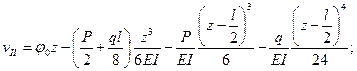
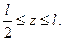
В полученных уравнениях прогибов неизвестна величина φ0. Для ее определения используем условие, что на правой опоре прогиб равен нулю; так как правая опора принадлежит второму участку, то, подставляя z = l в уравнение прогибов второго участка и приравнивая прогиб нулю, получим

Решая это уравнение относительно φ0, найдем
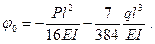
Подставив значение φ0 в уравнения прогибов, окончательно получим:
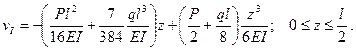
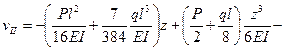
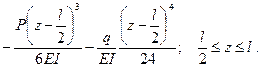
Найдем теперь прогиб посередине пролета. Положив 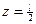 по первому уравнению, получим
по первому уравнению, получим
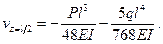
Данную величину можно определить также и из второго уравнения, так как середина пролета принадлежит и второму участку. Легко заметить, что два последних члена второго уравнения при 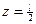 обращаются в нуль, поэтому получим тот же результат. Если в этой задаче положить
обращаются в нуль, поэтому получим тот же результат. Если в этой задаче положить 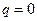 , то прогиб в балке от сосредоточенной силы в середине пролета (рис. 235, б) равен
, то прогиб в балке от сосредоточенной силы в середине пролета (рис. 235, б) равен
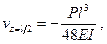
а угол поворота на опоре
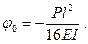
 § 80. МЕТОД МОРА ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
§ 80. МЕТОД МОРА ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕМЕЩЕНИЙ
 В предыдущих параграфах настоящей главы определялись перемещения в балках с прямой осью. Для брусьев с ломаной осью или для системы, состоящей из нескольких стержней, применение описанных выше методов вызывает затруднения. Более универсальным является метод Мора, который широко применяется в теории расчета стержневых систем. Этот метод основан на известном из теоретической механики принципе возможных перемещений.
В предыдущих параграфах настоящей главы определялись перемещения в балках с прямой осью. Для брусьев с ломаной осью или для системы, состоящей из нескольких стержней, применение описанных выше методов вызывает затруднения. Более универсальным является метод Мора, который широко применяется в теории расчета стержневых систем. Этот метод основан на известном из теоретической механики принципе возможных перемещений.
Для удобства применения этого метода условимся относительно обозначений. Перемещение какой-либо точки по определенному направлению от какой-либо силы или группы сил обозначается греческой буквой Δ, а перемещение от силы, равной единице, – буквой δ. Кроме того, каждое из перемещений обозначается двумя значками, например ΔКР , ΔК , δmn , и т. п. Первый значок обозначает точку, для которой определяется перемещение и вместе с тем направление этого перемещения, а второй значок определяет причину, вызвавшую данное перемещение.
Так, например, ΔКР может обозначать перемещение точки К по вертикали от группы сил Р. Если в какой-либо точке приложена сила Рк по определенному направлению, то величину ΔKP можно рассматривать как перемещение по направлению силы РK от нагрузки, обозначаемой индексом Р.
Перемещение по направлению силы РК от температуры соответственно следует обозначать Δkt . Второй значок t показывает, что причиной, вызвавшей перемещение, является температура.
Под обозначением δmn нужно понимать перемещение по направлению воздействия m от n-й единичной силы. Если перемещение берется по направлению момента, то оно представляет собой угол поворота.
Такие обозначения обладают универсальностью, их можно понимать в обобщенном смысле не только как линейное или угловое, но и как групповое перемещение, например сближение каких-либо двух точек и т. п.
В теоретической механике начало возможных перемещений применяется к абсолютно жестким телам. По этому принципу в положении равновесия работа всех сил на любых бесконечно малых возможных (допускаемых связями) перемещениях равна нулю:
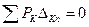 , (9.14)
, (9.14)
где 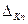 составляющая возможного перемещения точки приложения силы Рк по направлению этой силы от п -го возможного перемещения системы.
составляющая возможного перемещения точки приложения силы Рк по направлению этой силы от п -го возможного перемещения системы.
| Рис. 243 |
Уравнение (9.14) применяется для исследования равновесия твердых тел, в частности для определения опорных реакций.
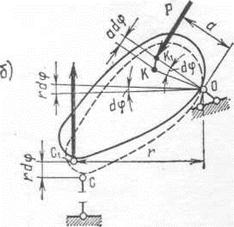
Для примера рассмотрим жесткий диск, показанный на рис. 243, а.
Поставим задачу определить опорную реакцию R. Разрежем опорный стержень и сообщим диску возможное бесконечно малое перемещение. При этом диск повернется вокруг точки О на бесконечно малый , гол dφ. Точка К приложения силы Р переместится в точку К1, а точка С приложения реакции R переместится в точку С1 (рис. 243, б).
Перемещения точек приложения сил Р и R по направлению их действия от этого угла поворота составят
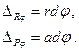
Составляя уравнение принципа возможных перемещений, имеем
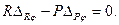
Знак минус перед последним членом поставлен потому, что перемещение ΔPφ направлено в сторону, противоположную направлению действия силы Р.
Решая полученное уравнение относительно R, найдем
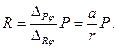
Точно такой же результат получится, если использовать обычное уравнение равновесия в виде
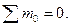
Рассмотрим теперь не абсолютно жесткое, а деформируемое упругое тело. Если задать точкам такого тела, находящегося в равновесии, бесконечно малые перемещения, при которых появляются деформации, то в теле возникнут внутренние силы, которые также произведут работу.
В этом случае уравнение принципа возможных перемещений (9.14) запишется так *:
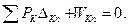 (9.15)
(9.15)
Здесь первое слагаемое, так же как и в уравнении (9.14), представляет собой работу внешних сил на заданных возможных перемещениях, а второе слагаемое – работу внутренних сил также на возможных перемещениях внутренних частиц тела.
Предположим, что при возможных перемещениях величина и, направление всех внешних и внутренних сил остаются неизменными, такими же, как в исходном состоянии, т. е., как обычно, ввиду малости перемещений здесь не учитывается перераспределение усилий, связанное с деформацией тела.
Следовательно, в качестве возможных можно брать и конечные, но малые перемещения, например определяемые на основе гипотез сопротивления материалов прогибы и углы поворота от какой-либо конкретной нагрузки.
Рассмотрим ломаный брус, показанный на рис. 244, а, под действием силы Рк = 1. В качестве возможных перемещений примем перемещения, которые произойдут вследствие деформации одного малого элемента длиной ds, расположенного в пределах, например, вертикальной стойки (рис. 244, а). Предположим, что деформация элемента ds произошла от какой-либо группы сил. При обозначении внутренних сил и перемещений от этой нагрузки будем применять индекс Р. Так, например, внутренние силы в элементе ds от этой группы сил будут NP, МP и QP. Перемещение по направлению силы Рк = 1 (рис. 244, б) обозначим dΔKP. Оно равно проекции полного перемещения точки К

* Предполагается, что при деформации не происходит рассеяние энергии.
(отрезок KK1) на направление действия силы Рк = 1.
Пользуясь формулой (9.15) для рассматриваемого случая, имеем
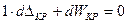 (9.16)
(9.16)
Здесь dWKP – элементарная работа внутренних сил 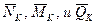 , вызванных силой РК = 1 на перемещениях (Δds)P, dφP и сдвигах γP, которые возникли вследствие деформации одного элемента ds. Эта деформация произошла от некоторой группы сил Р (на рис. 244 они не показаны). Черточка, проведенная над обозначениями
, вызванных силой РК = 1 на перемещениях (Δds)P, dφP и сдвигах γP, которые возникли вследствие деформации одного элемента ds. Эта деформация произошла от некоторой группы сил Р (на рис. 244 они не показаны). Черточка, проведенная над обозначениями 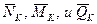 , показывает, что соответствующие значения найдены от единичной силы.
, показывает, что соответствующие значения найдены от единичной силы.
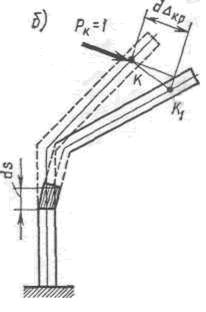
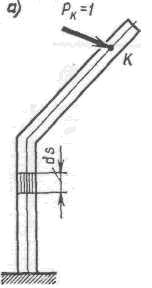
| Рис. 244 |
Общую деформацию элемента ds можно представить в виде трех составляющих: удлинения ΔdsP (рис. 245, а), угла поворота сечения dφP (рис. 245, б) и сдвигов каждого из волокон γP (рис. 245, в).
Внутренние силы, возникающие в элементе ds от силы РK = 1, являются по отношению к нему внешними силами. Нормальная сила 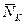 и момент
и момент 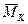 на перемещениях (Δds)P и dφP совершают работу, равную (рис. 245)
на перемещениях (Δds)P и dφP совершают работу, равную (рис. 245)
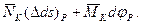 (а)
(а)
Касательные напряжения распределены в сечении по сложному закону. Для определения работы сил 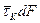 на перемещениях γPds составим интеграл:
на перемещениях γPds составим интеграл:
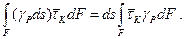 (б)
(б)
Складывая выражения (а) и (б), получим работу сил NK и МК и усилий, вызывающих сдвиги в элементе ds. Поскольку эти силы но отношению к элементу ds являются внешними, то работа внутренних сил будет иметь обратный знак. В силу сказанного второе слагаемое, входящее в формулу (9.16), определяется равенством

Подставляя это выражение в (9.16) и определив dΔKP, найдем
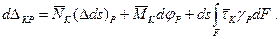 (9.17)
(9.17)
Вычислим вначале интеграл, входящий в формулу (9.17). Учтя, что 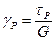 , а также что
, а также что 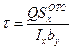 , получим
, получим
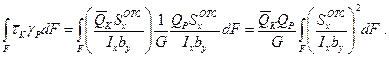
Обозначим, как это было сделано в § 67,
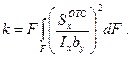 (9.18)
(9.18)
| Рис. 245 |
Эта величина является безразмерной и для каждого сечения может быть вычислена по формуле (9.18).
Подстановка дает
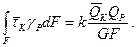 (9.19)
(9.19)
Учитывая далее, что
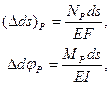
после подстановки этих выражений и выражения (9.19) в формулу (9.17) получим
 (9.20)
(9.20)
Это перемещение возникает вследствие деформаций только одного малого элемента ds. Для учета деформаций всей системы в целом необходимо проинтегрировать (9.20), распространяя интегрирование на все элементы системы. Принято такой интеграл снабжать индексом «s» внизу, который символизирует учет деформации всей системы в целом. Таким образом, имеем формулу Мора
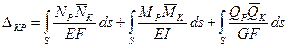
Необходимо иметь в виду, что входящие в формулу Мора силовые факторы берутся в произвольной точке и поэтому представляют собой аналитические функции от координат произвольных точек.
Для шарнирно-стержневых систем, в которых стержни работают только на осевую силу, в формуле Мора (9.21) отличен от нуля только первый интеграл. В этом случае нормальная сила по длине каждого стержня обычно не меняет своей величины, поэтому подынтегральное выражение как постоянная величина выйдет за знак интеграла, а сам интеграл превратится в длину стержня. Учитывая деформацию всех стержней, получим
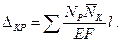
Так как рассматриваются только плоские стержневые системы, то значки у М, N, Q и I опускаем, т. е. считается, что Мx = М, Qy = Q, Ix = I и т. п.
Остановимся теперь на технике вычисления интегралов Мора.
Заметим, что все три интеграла формулы Мора (9.21) имеют одинаковый вид, который в общем виде можно представить так:
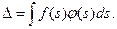 (9.22)
(9.22)
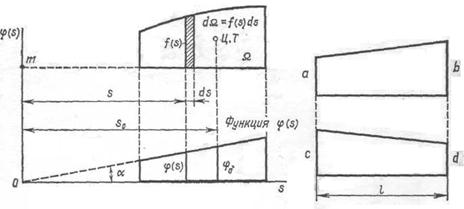
Предположим, что одна из подынтегральных функций является линейной функцией, а вторая, например f(s), – произвольной. На рис. 246 показан примерный вид функций f(s) и q(s).
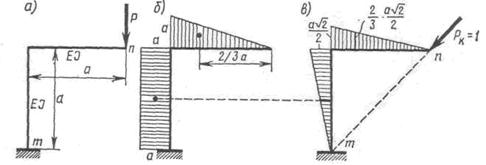 Из рис. 246 видно, что
Из рис. 246 видно, что
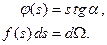
Подставляя эти выражения в интеграл (9.22), получим
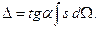
Величина интеграла численно равна статическому моменту площади Ω эпюры f(s) относительно точки т (рис. 246), который в свою очередь равен площади всей эпюры, помноженной на отрезок s0, поэтому
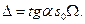
Но так как s0tgα = φ0, где φ0– ордината в эпюре φ(s), взятая под центром тяжести площади Ω, то
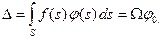
| Рис. 246 |
| Рис. 247 |
 Таким образом, любой из интегралов Мора в пределах участка, на котором эти две эпюры непрерывны и одна из них линейная, равен площади криволинейной эпюры, помноженной на ординату линейной эпюры, взятую
Таким образом, любой из интегралов Мора в пределах участка, на котором эти две эпюры непрерывны и одна из них линейная, равен площади криволинейной эпюры, помноженной на ординату линейной эпюры, взятую
под центром тяжести площади Ω. Эпюры от единичных сил всегда линейные, поэтому при наличии нескольких участков
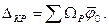 (9.23)
(9.23)
Полученное выражение носит название формулы Верещагина, автора данной формулы.
Если обе эпюры прямолинейные, то в любой из них можно брать площадь и в другой – ординату под центром тяжести первой эпюры.
| Рис. 248 |
Рассмотрим частный, но вместе с тем широко распространенный случай, когда на каком-то участке обе эпюры имеют вид трапеции (рис. 247).
В этом случае
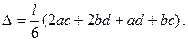 (2.24)
(2.24)
Пример 1. Определить, на сколько изменится расстояние между точками m и n в результате деформации от изгиба рамы, показанной на рис. 248, а, под действием силы Р=1 Жесткости обоих стержней одинаковые и равны EJ. При определении перемещений в рамах обычно пренебрегают влиянием нормальных и поперечных сил и формулой Мора (9.21) учитывают только один интеграл, определяющий изгибные деформации:
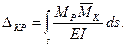
Здесь МP – моменты от заданной нагрузки. Эпюра этих моментов показана на рис. 248, б. Эпюру 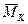 строим от силы, приложенной в точке п по направлению к точке т (рис. 248, в).
строим от силы, приложенной в точке п по направлению к точке т (рис. 248, в).
Пользуясь формулой Верещагина, находим
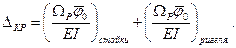
Вычисления дают