ВНЕЦЕНТРЕННОЕ ДЕЙСТВИЕ ПРОДОЛЬНОЙ СИЛЫ
| Рис. 288 |
1. Определение напряжений. Рассмотрим случай внецентренного сжатия массивных колонн (рис. 288). Такая задача очень часто встречается в мостостроении при расчете опор мостов и в гражданском строительстве при расчете колонн зданий.
Предположим, что сжимающая сила Р приложена в точке с, которая имеет координаты хР и уР, отсчитанные относительно главных центральных осей инерции.
От этой силы в произвольном сечении стержня возникают нормальная сжимающая сила N = – Р и два изгибающих момента, которые в соответствии с принятым правилом знаков будут отрицательными, так как они вызывают сжатие в точках, лежащих в первой четверти:
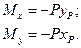
Напряжение в произвольной точке К, лежащей в положительной четверти произвольного поперечного сечения, равно
 (11.10)
(11.10)
По формуле (11.10) можно найти напряжение в любой точке сжатой колонны; для этого необходимо величины хну брать с учетом знака.
| Рис. 289 |
| Рис. 290 |
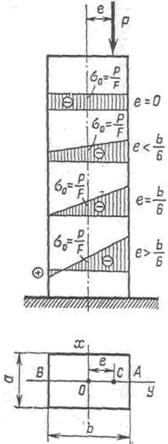
Рассмотрим теперь частный случай внецентренного сжатия колонны прямоугольного сечения, когда один из эксцентриситетов равен нулю. Пусть сила расположена на оси Оу (хР = 0, уР = е), как это показано на рис. 289. Подставляя эти значения в формулу напряжений (11.10), для крайних волокон получим
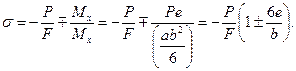 (11.11)
(11.11)
Из этой формулы видно, что при е = 0 напряжения во всем сечении одинаковые. Если  , то напряжения во всем сечении одного знака (сжатие). В частности, когда
, то напряжения во всем сечении одного знака (сжатие). В частности, когда  , напряжения в точках А и В равны:
, напряжения в точках А и В равны:

Если, наконец,  , то нейтральная ось расположена внутри сечения. Она разделит его на две части: в одной из них напряжения сжимающие, а в другой – растягивающие. Для этих четырех случаев на рис. 289 показаны эпюры напряжений. Таким образом, если не хотят, чтобы в поперечном сечении появлялись растягивающие напряжения, то эксцентриситет нельзя допускать больше чем
, то нейтральная ось расположена внутри сечения. Она разделит его на две части: в одной из них напряжения сжимающие, а в другой – растягивающие. Для этих четырех случаев на рис. 289 показаны эпюры напряжений. Таким образом, если не хотят, чтобы в поперечном сечении появлялись растягивающие напряжения, то эксцентриситет нельзя допускать больше чем  .
.
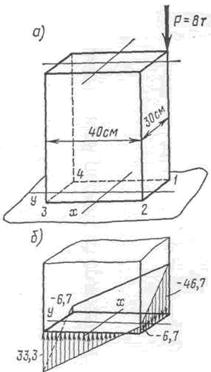
Пример. Определить напряжения и построить их эпюру в поперечном сечении колонны (рис. 290, а).
Найдем изгибающие моменты:
Мх = + 8000 · 20 = 160000 кгс · см;
Мy = + 8000 · 15 = 120000 кгс · см.
Найдем геометрические характеристики сечения: площадь сечения
F = 40 · 30= 1200 см2;
моменты сопротивления:
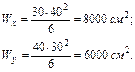
Найдем теперь напряжения в четырех угловых точках поперечного сечения:

По этим значениям σ построена эпюра напряжений (рис. 290, б).
2. Определение положения нулевой линии. Для того чтобы определить положение нулевой линии, преобразуем формулу (11.10). Подставляя в эту формулу значения моментов, получим
 .
.
Величины, стоящие в знаменателе второго и третьего слагаемых, представляют собой квадраты радиусов инерции сечения, т. е.

Следовательно,
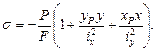 (11.12)
(11.12)
Этой формулой, так же как и формулой (11.10), можно пользоваться для определения напряжений в любой точке поперечного сечения ко» лонны. Обозначим координаты любой точки нулевой линии  и
и  Если эти координаты подставить в уравнение (11.12) и учесть, что напряжения в точках нулевой линии равны нулю, то после сокращения на величину
Если эти координаты подставить в уравнение (11.12) и учесть, что напряжения в точках нулевой линии равны нулю, то после сокращения на величину  получим уравнение нулевой линии
получим уравнение нулевой линии
 (11.13)
(11.13)
По этому уравнению можно определить отрезки, отсекаемые нулевой линией на осях координат. Обозначим эти отрезки (рис. 291, а) через  и
и 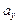 . Если
. Если

| Рис. 291 |
положить  , то из уравнения (11.13) получим
, то из уравнения (11.13) получим
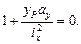
Точно так же для случая 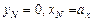 имеем
имеем

Решая эти уравнения, получим отрезки, отсекаемые нейтральной линией на осях координат:

Вместе с тем можно решить обратную задачу, выразив координаты точки приложения силы Р при заданных отрезках, отсекаемых нулевой линией на осях координат:
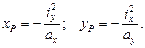 (11.15)
(11.15)
Отметим интересную зависимость величин хР и ах, а также уР и аx,. Если силу приложить в точке с координатами ах и ау, то нулевая линия отсечет отрезки на осях координат, равные соответственно xP и уP. Если сила приложена в точке 1 (рис. 291, б), а соответствующая нулевая линия занимает положение I-I, то при силе, поставленной в точку 2, нулевая линия займет положение II-II.
Рассмотрим теперь некоторые характерные особенности, связанные с поведением нулевой линии при различных положениях силы Р (рис. 292).

| Рис. 292 |
| Рис. 293 |
Если сила Р приложена в точке, лежащей на оси Оу, то нулевая линия отсекает на оси Ох отрезок, равный бесконечности:
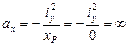 .
.
Это означает, что нулевая линия будет параллельна оси Ох.
Представим себе, что сила Р перемещается по оси Ох от центра тяжести к краю сечения. В этом случае нулевая линия перемещается из бесконечности по направлению к сечению, оставаясь при этом все время параллельной оси Оу. Точно так же если сила перемещается по оси Оу, то нулевая линия перемещается поступательно, оставаясь все время параллельной оси Ох.
Так, например, когда сила последовательно приложена в точках 1, 2, 3, 4, (рис. 292), нулевая линия соответственно занимает положения I-I, II-II, III-III, IV-IV и т. д.
Рассмотрим теперь случай, когда сила Р перемещается по некоторой прямой ОЕ, проходящей через центр тяжести сечения, но не совпадающей ни с одной из главных осей инерции. В этом случае нулевая линия (рис. 292) будет также перемещаться параллельно самой себе. В самом деле, из уравнений (11.14) вытекает соотношение
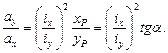
Отсюда можно сделать вывод, что тангенс угла наклона нулевой линии  не зависит от численного значения координат точки приложения силы, а зависит от их отношения.
не зависит от численного значения координат точки приложения силы, а зависит от их отношения.
Рассмотрим теперь еще одну задачу, которая имеет большое значение в дальнейших выводах. Пусть сила Р перемещается по некоторой прямой АВ, не проходящей через центр тяжести сечения (рис. 293). Для двух крайних случаев, когда сила приложена в точках А и В, нулевые линии параллельны соответствующим осям Ох и Оу. Пусть эти линии пересекаются в некоторой точке D. Так как эта точка принадлежит двум нулевым линиям, то напряжения в ней от двух сил, одновременно приложенных в точках А и В, равны нулю. Приложим теперь силу Р в точке С, лежащей на прямой АВ. Эту силу можно разложить на две параллельные составляющие РА и РB, приложенные к точкам А и В. От этих двух составляющих, а следовательно, и от их равнодействующей напряжения в точке D будут равны нулю. Так как точка С была взята произвольно, то при любом положении силы Р на прямой АВ напряжение в точке D равно нулю.
Отсюда можно сделать заключение, что при движении груза по прямой АВ нулевая линия вращается вокруг точки D.
Полученные в этом параграфе выводы о поведении нулевой линии, связанные с перемещением по сечению сжимающей силы, будут использованы для последующего анализа внецентренного сжатия колонн.
 § 93. ЯДРО СЕЧЕНИЯ
§ 93. ЯДРО СЕЧЕНИЯ
 Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила Р перемещается из центра тяжести поперечного сечения по прямой ОА (рис. 294), в это время нулевая линия также будет перемещаться из бесконечности в направлении к центру тяжести сечения, оставаясь все время параллельной первоначальному своему положению.
Рассмотрим случай внецентренного сжатия массивной колонны произвольного поперечного сечения. Предположим, что сила Р перемещается из центра тяжести поперечного сечения по прямой ОА (рис. 294), в это время нулевая линия также будет перемещаться из бесконечности в направлении к центру тяжести сечения, оставаясь все время параллельной первоначальному своему положению.
| Рис. 294 |
| Рис. 296 |
| Рис. 295 |
Наступит такой момент, когда нулевая линия в какой-либо точке коснется сечения и займет положение I-I. Этому положению нулевой линии на прямой ОА соответствует точка 1, к которой приложена сила Р. Если груз передвинуть за точку 1, еще дальше от центра тяжести, то нулевая линия дополнительно переместится, войдет внутрь поперечного сечения и разделит сечение на две части: сжатую и растянутую. Таким образом, точка 1 является граничной точкой, за пределы которой нельзя перемещать груз, если мы не хотим, чтобы в поперечном сечении появлялись растягивающие напряжения.
Точно так же на прямых ОВ и ОС можно определить точки 2 и 3, которые обладают теми же свойствами, что и точка 1.
Касательные II-II и III-III являются нулевыми линиями для тех случаев, когда сила приложена в точках 2 и 3.
Если мысленно провести бесчисленное множество прямых, исходящих из течки О, и определить на них граничные точки, то геометрическое место этих точек образует кривую, которая вокруг центра тяжести сеченияочертит некоторую область, называемую ядром сечения. Всякая сжимающая сила, приложенная где-либо внутри ядра сечения, вызываетво всем сечении только сжимающие напряжения. От растягивающей силы, приложенной внутри этого ядра, возникают только растягивающие напряжения.
Таким образом, ядром сечения называется область, очерченная вокруг центра тяжести и характерная тем, что всякая продольная сила, приложенная внутри этой области, вызывает во всех точках поперечного сечения напряжения одного знака.
В тех случаях, когда колонна изготавливается из материала, плохо работающего на растяжение (например, бетон, камень, кирпичная кладка и т. п.), очень важно знать заранее размеры ядра сечения и его форму.
Для того чтобы построить ядро сечения, необходимо рассмотреть всевозможные положения касательных к контуру сечения и, предполагая, что

эти касательные представляют собой нулевые линии, найти по отношению к главным осям сечения соответствующие координаты граничных точек ядра сечения, а затем по этим точкам очертить само ядро.
Рассмотрим часто встречающийся случай, когда сечение представляет собой многоугольник (рис. 295). Предположим сначала, что нулевая линияI-I совместилась с гранью AD. Найдем отрезки, отсекаемые ею на главных осях, и, применяя формулы (11.15), вычислим координаты ур и хр точки приложения силы, при которых имеет место указанное положение нулевой линии. Пусть это будет точка 1. Точно такимже образом можно определить точку 2, которой соответствует нулевая линия II-II, совпадающая с гранью DB.
В предыдущем параграфе было сказано, что при движении силы по прямой нулевая линия вращается вокруг некоторой точки. Справедливо и обратное положение; если нулевая линия вращается вокруг какой-либо точки, то сила в сечении перемещается по прямой. Таким образом, если перевести касательную из положения I-I в положение II-II, вращая ее вокруг точки D, то сила должна пройти прямую 1-2, которая, и образует одну из сторон ядра сечения.
Предположим теперь, что все сечение обогнули касательными, проведенными через угловые точки или грани внешнего контура, и вычислили положение вершин ядра сечения соответственно нулевым линиям I-I, II-II, III-III, IV-IV, V-V, VI-VI. Если полученные таким образом вершины 1, 2, 3, 4, 5 и 6 соединить прямыми линиями, то область, лежащая внутри этого контура, и будет представлять собой ядро сечения.
Таким образом, при сечении, имеющем форму многоугольника, ядро сечения также будет многоугольник. Однако в тех случаях, когда контур сечения имеет внутренние углы, как это показано, например, на рис. 296, число сторон у ядра сечения не совпадает с числом сторон самого сечения. Это объясняется тем, что нулевую линию нельзя совместить с ребром АВ и ВС, так как в этом случае она не будет являться касательной к контуру сечения, а будет его пересекать.

| Рис. 297 |
Рассмотрим примеры построения ядра сечения для ряда наиболее распространенных случаев.
1. На рис. 297, а показано прямоугольное сечение со сторонами b и h. Рассмотрим четыре положения касательной, совмещенной со сторонами прямоугольника. Для касательной I-I отрезки, отсекаемые на осях координат, равны ах = ∞, ау = h/2. Координаты первой , вершины ядра сечения соответственно определяются по формулам (11.15):

Таким образом, точка 1 лежит на оси Оу на расстоянии h/6 от оси Ох, причем это расстояние откладывается в сторону, противоположную касательной I-I. Точно так же точка 3 для касательной III-III будет лежать на оси у и также на расстоянии h/6 от оси Ох, Если теперь повторить все рассуждения по отношению к касательной II-II и IV-IV и найти вершины ядра сечения, то получим  .
.
Для того чтобы завершить построение ядра сечения, необходимо обогнуть касательной весь контур сечения. Это можно сделать путем вращения касательных около угловых точек. Каждому такому вращению соответствует прямая линия у ядра сечения. Таким образом, ядро сечения имеет вид ромба, как это показано на рис. 297, а.
 2. Рассмотрим построение ядра сечения для двутаврового профиля. Так же как в предыдущем случае, необходимо рассмотреть четыре положения касательных (рис. 297, б). Ввиду симметрии достаточно определить две вершины ядра сечения. Для точек, лежащих на оси у, имеем
2. Рассмотрим построение ядра сечения для двутаврового профиля. Так же как в предыдущем случае, необходимо рассмотреть четыре положения касательных (рис. 297, б). Ввиду симметрии достаточно определить две вершины ядра сечения. Для точек, лежащих на оси у, имеем

для двух других точек аналогично получим

| Рис. 298 |
Численные значения этих отрезков зависят от соотношения размеров двутавра. Ядро сечения для двутаврового профиля, так же как и для прямоугольника, имеет вид ромба.
3. Построить ядро сечения для круглого сплошного сечения. Ввиду того, что круг симметричен относительно центра (полярная симметрия), достаточно рассмотреть одно произвольное положение касательной (рис. 297, б). Расстояние до грани ядра сечения равно
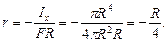
Таким образом, ядро сечения для круга радиуса R очерчено также по окружности радиуса r.
На рис. 298 показано ядро сечения для тавра. Система касательных к контуру сечения образует шестиугольник, поэтому и ядро сечения также имеет очертание шестиугольника.